baldin_kv_red_matematika_dlia_gumanitariev

Пример 4.8.

Z = sin (x y2)·ln ( y + x2).

Производнаяпонаправлениюиградиент

Предположим, что в каждой точке А некоторой области D задано значение скалярной физической величины W (температура, давление, влажность и т. п.). Тогда W называется скалярной функцией точки и записывается так W = W(A). Если в области D задана скалярная функция точки W(A), то говорят, что в этой области задано скалярное поле.

Если скалярное поле не зависит от времени, оно называется стационарным. В противном случае поле будет нестационарным, т. е. будет зависеть не только от точки А, но и от времени t.

Производнаяпонаправлению

В гиперпространстве, в котором задано поле W = W(x1, x2, …, xn) возьмем точку А(x1, x2, …, xn) и найдем скорость изменения функции при движении точки А в направлении некоторого вектора 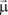. Этот вектор начинается в точке А, а углы между ним и координатными осями Х1, Х2, …, Хn (направляющие коси-

нусы) равны: cos w1, cos w2, …, cos wn.

Приращение DW, получаемое при переходе от точки А в точку А1, по направлению 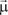равно:

121

DW = W(x1 + Dx1, x2 + Dx2, …, xn + Dxn) - W(x1, x2, …, xn).

Тогда

Производной от функции W(x1, x2, …, xn) в точке А(x1, x2, …, xn) по направлению 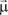называется предел

То есть производная характеризует скорость изменения функции по данному направлению.

В курсах математического анализа доказывается (см., например, [2]), что

Пример 4.9. Найти производную функции

в т. A(0, 1, 2, 1) по направлению к т. A1(2, 0, 1, )

Находим направляющие косинусы вектора :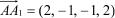

cos w1 = 0,6 2; cos w2 = -0, 16; cos w = -0, 16; cos w4 = 0,6 2.

Далее определяем частные производные исходной функции W и их значения в точке А, т. е.

Затем вычисляем искомую производную по направлению

Знак минус говорит о том, что функция в заданном направлении убывает. Вектор, координатами которого являются зна-

122

чения частных производных функции W(x1, x2, …, xn) в точке А(x1, x2, …, xn), называют градиентом функции и обозначают grad W, т. е.

или

Теперь формулу для производной по направлению можно переписать в виде скалярного произведения grad W на единич-

ный вектор = (cos w1, cos w2, …, cos wn), т. е.

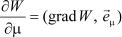или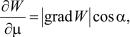

где — угол между вектором grad W и направлением .

Из последней формулы видно, что dW / d достигает своего максимального значения в том случае, когда = 0. Поэтому направление градиента совпадает с направлением вдоль которого функция меняется быстрее всего, т. е. grad W показывает направление скорейшего возрастания функции. А наибольшая скорость изменения функции W в точке А равна:

Пример. Найти наибольшую скорость возрастания функ-

ции в точке А(1, 2, -1, ).

Вначале находим частные производные

Затем получаем

и вычисляем 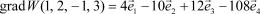и, наконец, находим наибольшую скорость возрастания функции

|grad W(A)| = 109,2.

12

4.3.некоторыеприложениядифференциальногоисчисления

4.3.1.ФормулаТейлора

Пусть некоторая функция y = f(x) имеет все производные до (n + 1)-го порядка включительно на некотором интервале, включающем точку x0. Найдем многочлен y = Pn(x) степени не выше n, значение которого в точке x = x0 равно значению функции y = f(x) в этой точке, а значение его производных до n-го порядка в точке x = x0 равны значениям соответствующих производных от функции y = f(x) в этой точке, т. е.

(4.1)

Искомый многочлен (более подробно см., например, [20,22]) будет иметь вид:

(4.2)

Через Rn(x) обозначим разность значений данной функции y = f(x)и многочлена, находимого по формуле (4.2), т. е. Rn(x) =

= f(x) – Pn(x).

Отсюда f(x) = Pn(x) + Rn(x), или

(4. )

где Rn(x) — это остаточный член, который может быть записан в разных формах. Мы приведем так называемую форму Лагранжа, которая имеет вид:

124

(4.4)

Здесь [ [x, x0] и ее можно представить в виде = x0 + + l(x - x0), где 0 < l < 1. Тогда формула для остаточного члена примет вид:

А формула

(4.5)

называется формулой Тейлора для функции y = f(x). Если в формуле (4.5) принять x0 = 0, то она примет вид:

(4.6)

Здесь 0 < l <1, а формулу (4.6) часто называют формулой Маклорена. Теперь найдем разложение функции y = ex по фор-

муле (4.6).

f (x) = ex; f (0) = 1; f (x) = ex; f (0) = 1; f 0(x) = ex;

f 0(0) = 1, …, f (n)(x) = ex; f (n)(0) = 1.

Эти данные подставляем в формулу (4.6) и получаем: , где 0 < l <1.

125

Если |x| # 1, то взяв n = 8, найдем оценку остаточного члена

. А если х = 1, то получим формулу для приближенного вычисления числа е [22], т. е.

Здесь верны первые четыре знака после запятой, так как ошибка не превосходит числа 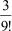или 10-5. Заметим, что какое бы ни было х, остаточный член 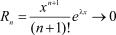при n → `,

т. е. . Поэтому при ;x, взяв достаточное число членов

разложения, по формуле (4.6) получим ex с любой необходимой степенью точности.

4.3.2.ПравилоЛопиталя

Данное правило помогает раскрывать неопределенности вида: 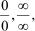его суть выражается теоремой [2, 20, 22].

Теорема 4.4 Лопиталя. Пусть функции f (x) и w (x) при x → x0 или x → ` совместно стремятся к нулю или к бесконечности. Если отношение производных этих функций имеет предел, то отношение самих функций тоже имеет предел, который равен пределу отношения производных, т. е.

(4.7)

(4.8)

Теперь рассмотрим конкретные примеры применения этого правила [4, 2 ].

Пример 4.10.

126

Ранее мы сводили этот предел ко второму замечательному пределу и пользовались тем, что ln x является непрерывной функцией. Заметим, что простота взятия данного предела кажущаяся, так как дифференцирование функций само опирается на знание пределов [2].

Пример 4.11.

Пример 4.12.

Пример 4.13.

Заметим, что если производные числителя и знаменателя одновременно стремятся к нулю или к бесконечности можно применять правило Лопиталя еще раз, а в случае необходимости и далее.

Пример 4.14.

Пример 4.15.

127

Формулы (4.7) и (4.8) справедливы только в том случае, если предел, стоящий справа (конечный или бесконечный), существует. Приведем пример, когда отношение функций имеет предел, а отношение их производных не стремится ни к какому пределу.

Пример 4.16.

А предел производных равен:

При x → ` этот предел колеблется между 0 и 2 и поэтому не имеет предела. То есть к данному примеру правило Лопиталя применить нельзя, оно не является универсальным.

При помощи правила Лопиталя можно раскрывать другие неопределенности, например:

Эти случаи сводятся к рассмотренным нами неопределен-

ностям .

Рассмотрим некоторые примеры.

Пример 4.17.

Это случай 0 · `.
Преобразуем данный предел к виду	, т. е. привели

исходный предел к случаю .

Теперь можно применить правило Лопиталя

128

Пример 4.18.

т. е., имеем случай ` – `. Исходный предел преобразуем к виду

т. е. мы пришли к случаю , поэтому применяем правило Лопиталя

Пример 4.19.

, т. е., имеем случай 1`. Рассмотрим предел

, а это случай , поэтому к последнему пределу применимо правило Лопиталя.

Поэтому исходный предел
Пример 4.20.
Найти	, т. е., имеем случай 00.
Рассмотрим	предел	, т. е.

пришли к случаю . Теперь к последнему примеру применяем правило Лопиталя

129

Поэтому исходный предел равен

4.3.3.Асимптоты

Прямая L называется асимптотой графика функции y = f (x), если расстояние d от переменной точки А функции до этой прямой при удалении точки А в бесконечность стремится к нулю (рис. 4.5) [2, 6, 22].

Рис. 4.5

Различают вертикальные асимптоты (параллельные оси 0у) и наклонные.

Сначала рассмотрим вертикальные асимптоты. Из определения асимптоты следует, что если

, или , или ,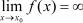

то прямая x = x0 является асимптотой функции y = f (x) и наоборот, если прямая x = x0 есть асимптота кривой y = f (x), то существуют указанные выше пределы.

То есть для нахождения вертикальных асимптот надо найти такие значения x = x0, при приближении к которым фун-

1 0