Методическое пособие 438

q CU0 0SU0 const . d1

Работа внешних сил приведет к увеличению энергии конденсатора, которую в этом случае удобно рассчитать по формуле

	q	2		1			1
W
	2					C
			C		2			.
						1

С учетом выражений для заряда и емкости воздушного конденсатора, получим окончательно

A W 0SU2 02 (d2 d1). 2d1

Рассмотрим второй случай.

Конденсатор соединен с источником, поэтому при любых манипуляциях разность потенциалов на его зажимах остается постоянной и равной U0 , при этом заряд может

изменяться. При раздвижении пластин внешняя сила равна и противоположна силе электростатического взаимодействия и ее работа определяется интегралом

2

A Fxdx.

1

Поскольку поле, создаваемое каждой из пластин, на небольших расстояниях однородно, то

		q1	F E1q2 ,
	где E		- напряженность поля, создаваемого одной из
	1	2S 0

пластин; q1 q2 q- абсолютное значение заряда пластин. Напряженность поля, созданного одной пластиной, вдвое меньше напряженности между обкладками конденсатора и равна

E1 U0 /2x.

171

Подставляя найденные соотношения в выражение для силы, получаем

F 0SU02 . 2x2

При раздвижении обкладок x изменяется в пределах от d1 до d2 , тогда

		0SU	2	d2	dx			0SU	2		1	1
A			0						0							4,2мкДж .
		2			x2			2			d		d
				d1							1			2

Аналогичный результат можно получить при энергетическом подходе.

В соответствии с уравнением энергетического баланса

W A Aист ,

где W - изменение энергии конденсатора; Aист - работа,

совершаемая источником, A - работа внешних сил.

Так как U0 const изменение заряда конденсатора

q С2 С1 U0 ,

отсюда

Aист qU0 U02 С2 С1 .

Изменение энергии конденсатора найдем по формуле

W U02 С2 С1 /2.

где С1 и С2 - соответственно конечная и начальная емкости конденсатора.

Из уравнения энергетического баланса с учетом того,

что С					1		1			, окончательно получим
	2	С		S
		1	0	d			d
					1			2
												0SU02	1		1
										A							.
												2				d2
													d1

172

3.3.4. Задачи для самостоятельного решения
		Первый уровень сложности
1.	Две	концентрические		металлические	сферы
радиусами	R1 10см и		R2 10,2см	образуют сферический

конденсатор. Промежуток между сферами заполнен парафином ( 2). Внутренней сфере сообщен заряд q 5 мкКл. Определить разность потенциалов между сферами. [4,4 кВ]

2. Разность потенциалов между пластинами плоского конденсатора U = 100 В. Площадь каждой пластины S = 200 см2, расстояние между пластинами d = 0,5 мм, пространство между ними заполнено парафином (ε = 2). Определите силу притяжения пластин друг к другу. [7,08 мН]

3. Две пластины площадью 100см2 погружены в масло, диэлектрическая проницаемость которого =2, и подключены к полюсам батареи с ЭДС, равной 300В. Какую работу необходимо совершить, чтобы после отключения батареи

расстояние между пластинами уменьшилось	от 5	до 1см?
[ 0,127мкДж]	C1 C2	2мкФ,
4. Конденсаторы электроемкостями

C3 3мкФ, C4 1мкФ соединены так, как указано на рис.78.

Разность потенциалов на обкладках четвертого конденсатора

U4 100В. Найти

заряды и

C2

C3

разности

потенциалов

на

C1

обкладках

каждого

конденсатора, а

также

общий

заряд и

разность

потенциалов

батареи

конденсаторов.

[200

C4

U4

мкКл;

120

мкКл;

12-

Рис.78

мкКл; 100мкКл; 110В; 60В; 40В;

220мкКл; 210В]

5. Определить

суммарную энергию

взаимодействия

точечных зарядов, расположенных в вершинах квадрата со

173

стороной a, для случаев: а) q1=q2=q; q3=q4=-q;					б) q1=q3=q;
q2=q4=q. Ха) W		q2 /4 0a; б) W		4 q2	/4 0a]
	2		2

6. Точечный заряд q = 3,0 мкКл находится в центре шарового слоя из однородного диэлектрика с проницаемостью= 3. Внутренний радиус слоя a=350 мм, внешний b=600 мм. Найти электрическую энергию в данном слое.

[W q2 /8 0 1/a 1/b 27мкДж ]
		Второй уровень сложности
	1. Найти емкость сферического конденсатора, радиусы
обкладок которого равны a и b					(b>a), если пространство
между обкладками заполнено: а) однородным диэлектриком с
проницаемостью ; б) диэлектриком, проницаемость которого
зависит от расстояния r				до центра конденсатора как /r,
где const. [а)		С 4 0 ab/ b a ; б)				С 4 0 /ln b/a ]
	2. Определить электроемкость						A
схемы,	представленной			на рис.79,
где	C 1пФ,	C	2	C 2пФ,		C1	C2
	1			3

C4 4пФ, C5 3пФ.

C5

Указание. Доказать, что если

C

C

A B

C3

C

1

3

, то

и,

B

4

C2

C4

следовательно,

емкость C5

при

Рис.79

определении общей емкости схемы значения не имеет.

3.Энергия заряженного плоского конденсатора, заполненного диэлектриком, равна W=2∙10-5Дж. После отключения конденсатора от источника напряжения

диэлектрик из конденсатора вынули, совершив при этом работу А=7.10-5Дж. Найти диэлектрическую проницаемость диэлектрика. [4,5].

4.Площадь каждой обкладки воздушного конденсатора 314 см2, расстояние между ними 2 мм. Напряженность поля между обкладками 60 кВ/м. Какую работу нужно совершить,

174

чтобы вдвинуть между обкладками конденсатора стеклянную пластинку, если она полностью заполняет конденсатор и конденсатор после зарядки отключен от источника напряжения? [ -086 мкДж].

5. Расстояние между обкладками плоского конденсатора равно 8 мм, площадь обкладок 62,8 см2. Какую работу нужно совершить, чтобы вдвинуть между обкладками конденсатора стеклянную пластинку той же площади и толщиной 6 мм, если конденсатор присоединен к источнику напряжения 600 В? [2,25 мкДж]

6.Уединенная металлическая сфера электроемкостью

С= 4 пФ заряжена до потенциала φ = 1 кВ. Определите энергию поля, заключенную в сферическом слое между сферой и концентрической с ней сферической поверхностью, радиус которой в 4 раза больше радиуса уединенной сферы. [1,5 мкДж]

7.	Сплошной	эбонитовый	шар (ε =	3) радиусом
R = 5	см заряжен	равномерно	с объемной	плотностью

ρ = 10 нКл/м3. Определите энергию электростатического поля, заключенную внутри шара. [0,164 пДж]

8.		Сферическую				оболочку		радиусом	R1 ,
равномерно заряженную зарядом							q, расширили до радиуса
R2 . Найти	работу,		совершенную				электрическими		силами.
[ A q2 /8	0	1/ R 1/ R		2	]
		1

175

Рис.П3

ПРИЛОЖЕНИЕ

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

1.1. Некоторые сведения о векторах

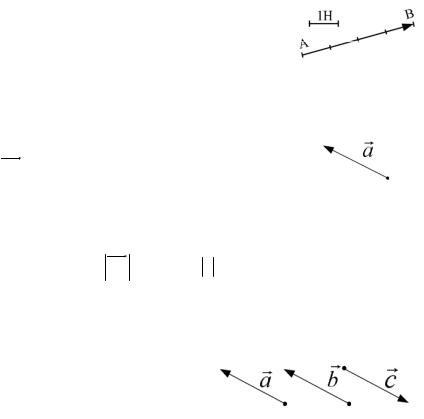
Векторной величиной, или

вектором, , направленный отрезок АВ при заданном масштабе, характеризует силу в 4 Н, направление которой совпадает с направлением АВ, указанным стрелкой (рис.П1).

Вектор, началом которого служит точка А, а концом точка В, обозначается

AB . Вектор обозначается также одной буквой. Эту букву печатают жирным шрифтом (а), или ставят над буквой стрелку (a) (рис.П2).

Длина вектора называется также

Рис.П1

Рис.П2

его модулем.

Обозначается: AB или АВ, a или а. Модуль есть скалярная

величина. Если начало и конец вектора совпадают, то отрезок АВ обращается в точку и теряет направление. Этот особый вектор называется нуль-вектором.

Два ненулевых вектора и называются

равными, если они равнонаправлены и имеют

один и тот же модульa=b (рис.П3). Два вектора,

имеющие равные модули и противоположно направленные,

называются противоположнымиa= c (рис.П3).

176

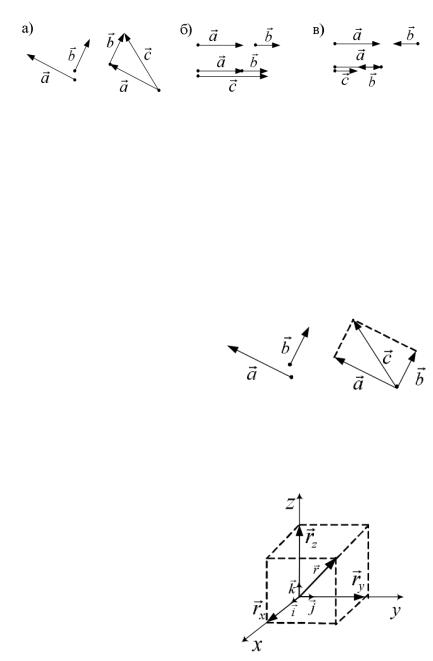
Рис.П4
Суммой двух вектров a	и b называется третий вектор
c =a+b , получаемый следующим		построением	(«правило
треугольника»): совмещаем	начало	вектора b	с концом

вектора a. Вектор, проведенный из начала вектора a в конец

вектора	b и	есть искомый вектор		c (рис.П4).	Сумма
противоположных векторов равна нуль-вектору.
«Правило			параллелограмма».	Суммарный	вектор
c =a+b	можно получить следующим построением: совместив
начала векторов a и b ,
достраиваем
параллелограмм.			Вектор,
проведенный		из	общего
начала	вдоль	диагонали и
будет искомым вектором c				Рис.П5

(рис.П5).

Суммой нескольких векторов a1,a2,a3...an , называется вектор, получающийся после последовательных сложений.

Вычесть вектор b (вычитаемое) из вектора c (уменьшаемое) значит найти построением новый вектор a (разность), который в сумме с

вектором b дает вектор c . Т.е. вычитание векторов есть действие обратное сложению.

Геометрической проек-цией вектора на

Рис.П6

177

Рис.П7

координатную ось называется вектор, полученный с помощью перпендикуляров, опущенных из начала и конца вектора на соответствующую координатную ось (рис.П6). В трехмерном пространстве это будут три проекции rx,ry ,rz , причем их

векторная сумма равна самому вектору r rx ry rz .

Через базисные вектора i, j,k , задающих направление

координатных осей:

r rxi ry j rzk ,

где rx,ry ,rz - алгебраические проекции вектора на

координатные оси, или координаты вектора (можно обозначать также через x, y, z).

Координаты вектора можно определить через углы

, , между	направлением вектора и соответствующими
осями координат
rx rcos ,	ry rcos ,

rz rcos .

Кроме того всякий вектор можно представить в виде

a aea ,

где а - модуль вектораa, ea -

единичный вектор или орт вектора a. Орты можно сопоставлять любым направлениям в пространстве.

Например, n - орт нормали к кривой или поверхности, - орт касательной к кривой и т.д.

Выражение вектора через радиусы-векторы его начала и конца (рис.П7)

r r2 r1 . 178

Если координаты векторов r2 и r1 , соответственно

x2, y2,z2 и x1,y1,z1 , то координаты вектора r находятся как разница между соответствующими координатами конца и

начала

r (x2 x1)i (y2 y1) j (z2 z1)k .

Длина вектора выражается через его координаты формулой

r (x2 x1)2 (y2 y1)2 (z2 z1)2 .

1.2. Скалярное и векторное произведение векторов

Скалярным произведением векторов a и b называется скаляр, равный произведению модулей этих векторов на

косинус угла между ними

a,b abcos .

Скалярное произведение обращается в нуль, если один из сомножителей есть нуль-вектор, или если векторы a и

b перпендикулярны.

Скалярный квадрат вектора есть квадрат его модуля.

a,a a2 a2 .

Скалярного куба (и тем более высших степеней) в векторной алгебре нет.

Скалярное произведение коммутативно, т.е. не зависит

от порядка сомножителей

a,b b,a ,

и дистрибутивно, т.е. произведение вектора a на сумму нескольких векторов равно сумме произведений вектора a на каждый из складываемых векторов, взятый в отдельности.

В декартовой системе координат выражение скалярного

произведения через координаты сомножителей имеет вид

a,b axbx ayby azbz .

179

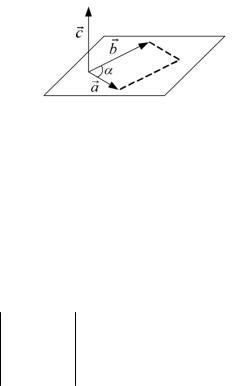
Векторным произведением вектора a на не

коллинеарный (не параллельный) ему вектор b называется третий вектор c , который строится следующим образом:

1) его модуль численно равен площади

параллелограмма, построенного на векторах a и b , т.е. он равен c absin ;

2)его направление перпендикулярно плоскости упомянутого параллелограмма;

3)при этом направление вектора c выбирается так, чтобы

векторы a,b,c составляли правовинтовую систему, т.е. его направление связано с направлением вращения от первого сомножителя ко второму

правилом винта (рис.П8)	Рис.П8
Обозначение векторного произведения:
c a,b	или c a b .

Векторное произведение дистрибутивно, но не обладает свойством коммутативности. Перестановка сомножителей вызывает изменение направления результирующего вектора на

противоположное

a,b b,a .

В декартовой системе векторное произведение можно представить в виде определителя

ij k

a,b x1 y1 z1 . x2 y2 z2

Смешанным (или векторно-скалярным) произведением трех векторовa,b,c (взятых в указанном порядке) называется скалярное произведение вектора a на векторное произведение

180