Учебное пособие 490

Для того чтобы найти площадь прямоугольника ОАСD,

надо определить абсциссу точки D, подставив значение t2 = p

6

в равенство x = 2 cos t . Получим x = 2 cos

p

=

2

3

=

3. Тогда

2

6

SOACD =

OA

×

OD

=1× 3 = 3.

Вернувшись

к

формуле

(*),

вычислим

SABC

=

4p + 3 3

-

3 =

4p -3

3

.

Окончательно

6

6

находим площадь заданной фигуры S = 2SABC

=

4p - 3

3

(ед.2 )

3

Пример 2. Вычислить площадь фигуры, ограниченной

окружностями ρ=2 cos φ, ρ = 3cos φ.

Решение.

Построим

данную

фигуру

в

полярной

системе координат (рис. 7). Так как

она

симметрична

относительно

полярной

оси,

то

достаточно

вычислить

площадь

половины

данной фигуры при изменении угла

от 0 до 90º, а затем полученный

результат удвоить.

Для вычисления

искомой площади воспользуемся

Рис. 7

формулой (3):

p

1

2

S = 2 ×

ò(3cos2 φ - 4cos2 φ)dφ=

2

0

					p										p
						2						5				2
				= òcos2 φdφ =												ò(1+ cos 2φ)dφ =
												2
					0										0
	5			1					p		5		æ p										5p
		æ			ö				2												ö			2
=		ç	φ +		sin 2φ ÷					=			ç					+ 0	- 0	- 0	÷	=		(ед. ).
	2			2							2				2								4
		è			ø				0			è									ø

Пример 3. Определить длину окружности x2 + y2 = 4 .

39

Решение.

Построим

кривую,

длину

которой необходимо найти(рис. 8). Так

как

график

функции

симметричен

относительно осей координат, то сначала

вычислим 4 1 часть длины дуги, а затем

домножим полученное значение на

Рис. 8

четыре.

-2

Здесь x Î[0, 2] ,

y =

4 - x2

, y ' =

.

Теперь

2 4 - x2

подставим найденные значения в формулу(11.4) нахождения

длины дуги

2

x2

2

2

x

2

æ p

ö

l = 4ò

1+

dx = 4ò

dx = 8arcsin

= 8

ç

- 0

÷ = 4p

- x

2

2

0

4

0

4 - x

2

0

è

2

ø

Пример 4. Определить длину кривой

ì

2

- 2) sin t + 2t cos t,

ïx = (t

0 £ t £ p.

í

-t2 ) cos t + 2t sin t,

ïy = (2

î

Решение. Найдем производные первого порядка от

функций x(t) и y(t) :

x ' = 2t sin t + (t 2 - 2) cos t + 2 cos t - 2t sin t = t 2 cos t,

y ' =1- 2t cos t - (2 -t 2 ) sin t + 2 sin t + 2t cos t = t 2 sin t.

Теперь подставим найденные значения в формулу(5)

нахождения длины дуги и получим

p

p

t3

p

p 3

l = ò

t4 cos2 t + t 4 sin2 t dt = òt 2dt =

=

.

0

0

3

0

3

Пример 5. Определить длину кардиоиды.

ρ = 2(1- cos φ),

0 £ φ £ π .

Решение. Построим данную кривую в

полярной системе координат (рис. 9).

Найдем

производную

первого

Рис. 9

порядка от функции и подставим в

40

формулу (6) нахождения длины дуги.

2(1- cos φ) ' = 2sin φ.

p	p
l = 2ò 4(1- cosj)2 + 4 sin 2 jdj =2ò		4 -8cosj + 4 cosj2 + 4 sin 2 j dj =
0	0
p	p		j			p
= 2ò 8(1- cosj)dj = 8òsin							= -16(0 -1) =16.
0	0	2				0
Пример 6. Вычислить		объем тела,						образованного
вращением	вокруг осиOx и		Oy				фигуры,	ограниченной

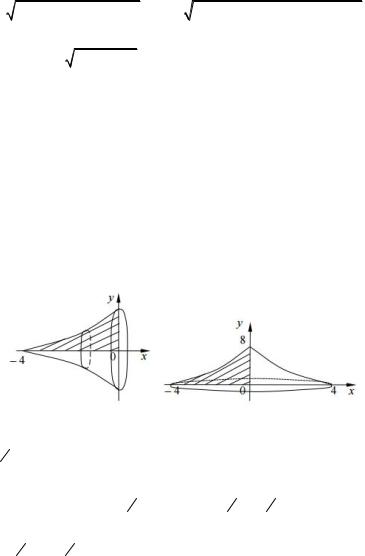
линиями y2 = (x + 4)3 , x = 0.

Решение. Рассмотрим вращение вокруг оси Ox (рис 10).

Так как фигура образована вращением вокруг осиOx , то (x + 4)3 £ y £ 0, а х изменяется от –4 до 0. Тогда по формуле (7)

0	(x + 4)	4			0	4	4	- 0 = 64p (ед. 2 ).
V = p ò (x + 4)3 dx = p					= p
	4					4
-4					-4

Рассмотрим вращение вокруг оси Oy (рис. 11).

Рис. 10

Рис. 11

Так как фигура образована вращением вокруг осиOy ,

то y2 3 + 4 £ x £ 0 , а у изменяется от 8 до 0. Тогда по формуле

(8)

			8		8								8	(y		43 +8y 2 3 +16)dy =
	V = p òx2dy =p ò(y							23 + 4)2 dy =p ò
			0		0								0
æ	7		24 y	5	ö		8	æ 3					24				ö				92
	3y 3			3							7				5				2				2
= p ç		+			+16 y ÷			= p ç		2		+		2		+16 ×8	÷	= 32		×p ×			(ед. ).
ç	7		5		÷			è 7					5				ø				35
è					ø		0

41

Задания для самостоятельного решения

1. Найти площадь фигуры, ограниченной: а) кривыми y =1- x2 и y = x2 - 7;

ìx = 3cos3 φ,

ï

б) астроидой í

ïîy = 3sin3 φ;

в) одной аркой циклоиды	ìx = 2(t -sin t),	− и осью Ox ,
	í
0 £ t £ 4p.	îy = 2(t - cos t)

Ответы: а) 63 ; б) 27 p ; в)12p .

38

2.Вычислить длину дуги:

а)	полукубической параболы y = x				32 от точки			O(0; 0)	до
точки A(4; 8) ;
б) кардиоиды r = 5(1- cos φ) .
Ответы: а)		8		(10 10 -1); б) 40 .
		27
3. Вычислить объем тела, образованного вращением фигуры:
а) вокруг оси Oy , ограниченной кривыми y =						2		и y = x2	;
					1+ x2
б)	вокруг			оси Ox , ограниченной			одной		аркой
	ìx = 3(t -sin t),
циклоиды í			= 3(t - cos t).
	îy

Ответы: а) 2 ln 2 - 1 ; б) 243p (8p 2 +1). 2

42

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Бугров Я.С. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. М.: Наука, 2009.

2.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов / Н.С. Пискунов. М.: Наука, 2005. Т.2.

3.Задачи и упражнения по математическому анализу для втузов: учеб пособие для студентов высш. техн. завед.; под ред. Б.П. Демидовича – М.: Астрель, 2001.

4.Виноградова И.А. Задачи и упражнения по математическому анализу/И.А. Виноградова, С.Н. Олехник, В.А. Садовничий - М., Высш. шк., 2000. – Кн. 1.

5.Сборник задач по высшей математике/К.Н. Лунгу [и

др.]- М.: Айртс-пресс, 2003.
6. Пантелеев	И.Н.	Высшая	математика.
Дифференциальные	уравнения.	Ряды:	практикум: учеб.

пособие / И.Н. Пантелеев. Воронеж: ГОУВПО «Воронежский государственный технический университнт», 2009.-215 с.

7.	Пантелеев И.Н.	Спецглавы высшей математики:
уравнения	матфизики: учеб. пособие		/ И.Н. Пантелеев.
Воронеж:	ГОУВПО	«Воронежский	государственный

технический университет», 2008.- 253 с.

8. Пантелеев И.Н. Высшая математика. Интегральное исчисление: практикум: учеб. пособие / И.Н. Пантелеев. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2009.- 231 с.

43

МЕТОДЫ ИНТЕГРИРОВАНИЯ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы по курсу "Высшая математика"

для студентов направления 20.01.03 "Техносферная безопасность"

(направленности «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды»)

очной формы обучения

Составитель Пантелеев Игорь Николаевич

В авторской редакции

Компьютерный набор И.Н. Пантелеева

Подписано к изданию 10.11.2017.

Уч.- изд. л. 2,6

ФГБОУ ВО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14

44