Учебное пособие 1852

5.23.5x3 1dx.

x2 5x

5.25. 2x3 1 dx. x2 4x 3

5.27.2x3 3dx.

x2 2x

2x3 8

5.29.x(x 4)(x 2) dx.

5.24.				x3 4			dx.
			x2	4x 3
5.26.			x3	2x 1
						dx.
				x2 x
5.28.			x3 2
					dx.
			x2	x 6

5.30. 2x3 x2 1 dx. x(x 3)(x 1)

Задача №6. Найти неопределённые интегралы.

5x 4

6.1.(x 2)(x 1)3 dx.

6.3.		5x			dx.
		(x 2)(x 1)3
6.5.		x2 7x		dx.
	(x 2)(x 1)3
6.7.		2x 1		dx.
	(x 1)(x 2)3

x 1

6.9.(x 1)(x 2)3 dx.

6.11.		x 1		dx.
		(x 2)(x 2)3
6.13.		x 4		dx.
		(x 2)(x 1)3

x 2

6.2.(x 2)x3 dx.

2 x

6.4.x 3 x3 dx.

x 2

6.6.(x 2)(x 2)3 dx.

x 3

6.8.(x 2)x3 dx.

x 1

6.10.(x 2)(x 1)3 dx.

6.12.		x		dx.
		(x 1)(x 2)3
6.14.	2x 1
			dx.
	(x 2)x3

50

6.15.				x 3					dx.
				(x 2)(x 2)3
6.17.				x 2				dx.
				(x 1)(x 2)3
6.19.				3x 1
					dx.
				(x 1)(x 2)3
6.21.				2x 3				dx.
				(x 2)(x 1)3
6.23.				3x 1				dx.
		(x 1)(x 2)3
6.25.				2x 1				dx.
		(x 2)(x 1)3

2x 3

6.27.(x 2)(x 1)3 dx.

6.29.	2x 3	dx.
	(x 2)x3

2x 1

6.16.(x 1)(x 2)3 dx.

3x 1

6.18.(x 2)(x 1)3 dx.

2x 1

6.20.(x 2)(x 1)3 dx.

3x 1

6.22.(x 2)(x 1)3 dx.

5x 4

6.24.(x 2)(x 1)3 dx.

4x 3

6.26.(x 1)(x 2)3 dx.

2x 5

6.28.(x 2)(x 2)3 dx.

3x 2

6.30.(x 1)(x 2)3 dx.

Задача №7. Найти неопределённые интегралы.

x 1

7.1. (x2 x 1)(x2 x 2) dx.

x 1

7.3. (x2 x 1)(x2 1) dx.

x1

7.5(x 3)2 (x2 2x 2) dx.

x 4

7.2. (x 1)2 (x2 9) dx.

x

7.4. (x 1)2 (x2 4x 5) dx.

x 1

7.6. (x2 x 1)(x2 1) dx.

51

7.7.																x													dx.											7.8.																	x 1																							dx.
	x								1						2		x				2		9																						2																				2
																																									(x								x 1)(x																			x 2)
7.9.																					x															dx.			7.10.																			x																dx.
										3)						2						2																										2			x 1)(x																2
	(x																		(x						2x 2)																		(x																										1)
7.11.															x 2																		dx.						7.12.																x 2																					dx.
																		2						2																									1)				2						2
								(x						1)						(x							1)																(x												(x											4x 5)
7.13.																			x 2																dx.					7.14.																					1																			dx.
																		2						2																												1)				2						2
								(x						1)						(x						x 1)																				(x												(x								4x 5)
7.15.														2x 6																			dx.							7.16.														4x 3																		dx.
																		2					2																																		2							2
								(x						1)						(x						9)																					(x						1)						(x							1)
7.17.																									x													dx.		7.18.															4x 1																		dx.
											2		x							1)(x							2			x																			(x 1)										2							2
								(x																										2)																										(x											1)
7.19.															x 1															dx.										7.20.												2x 3														dx.
										2					2				x 2)																																2				2		9)
												(x																																				x				(x
7.21.																x 1																	dx.							7.22.																		x 2																				dx.
										2					2		4x																																								2						2
									x			(x														5)																					(x						1)						(x							x 1)
7.23.																			x 1																dx.					7.24.														x 2																	dx.
								(x			2		x							1)(x							2			1)																	x			2		(x		2		x 2)
7.25.																					x 2																dx.			7.26.												x 2																		dx.
																			2						2	2x																							2				2
								(x						3)						(x														2)											x						(x				x 1)
7.27.															3x 2																		dx.							7.28.																		x 2																				dx.
									(x 1)2 (x2																	1)																				(x2 x 1)(x2 1)
7.29.																					x														dx.					7.30.																			x2																	dx.
																		2					2																												2	x 1)(x																	2
								(x						1)						(x						x 1)																			(x																										1)

52

3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Литература: [1, гл. 11, §§ 1 7].

3.1. Площадь криволинейной трапеции. Понятие определённого интеграла

К понятию определённого интеграла приводят многие задачи геометрии, механики и физики.

y

у0
							М
		A
															.						B
0
						1
																				xn=b
х	=a										...		k	...									x
0				0					2									n-1

Рис. 2

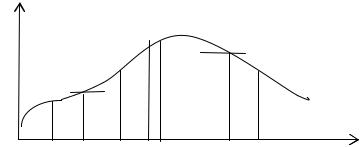
Пусть функция y = f(x) непрерывна на отрезке [a,b], причём f(x) >0. Рассмотрим фигуру, ограниченную осью Ох, графиком y = f(x), и двумя прямыми: x = a и x = b.

Эта фигура называется криволинейной трапецией, отрезок [a,b] оси Ох – её основанием (рис. 2).

Найдём площадь этой фигуры. Разобьём отрезок [a,b] на n частей произвольным образом. Через точки деления х1, х2,…хn-1 проведем прямые, параллельные оси Оу. Криволинейная трапеция при этом разбивается на n частей. Обозначим длины элементарных отрезков через хk:

x0 x1 x0 ; x1 x2 x1;... xk xk 1 xk ;... xn 1 xn xn 1.

В каждом из элементарных промежутков возьмём произвольную точку k :

x0 0 x1 ; x1 1 x2 ;... xk k xk 1 ;...xn 1 n 1 xn .

53

Вычислим значения функции f(x) в этих точках: f 0 , f 1 ,... , f k ,..., f n 1 .

Каждую элементарную полоску с основанием xk заменим прямоугольником с тем же самым основанием xk и высотой f( k ) (k = 0, 1, 2,…n-1). Площадь каждого такого прямоугольника равна f( k ) хk.

При этом криволинейная трапеция заменяется ступенчатой фигурой, площадь которой равна сумме площадей элементарных прямоугольников:

Sn f 0 x0 f 1 x1 ... f k xk ... f n 1 xn 1

n 1

или Sn f k xk .

k 0

Ясно, что площадь Sn ступенчатой фигуры не равна площади криволинейной трапеции, а является лишь приближённым значением искомой площади. Очевидно, что это приближение будет тем более точным, чем меньше длина частичных интервалов (и больше n). Полоски становятся уже, т.е. ломаная линия будет теснее примыкать к кривой y f (x) .

За площадь криволинейной трапеции принимают предел, к которому стремиться Sn, когда разбиение отрезка a, b делается сколь угодно мелким (если такой предел существует):

S	lim		Sn или
	max xk	0
			n 1
S	lim	0	f (k ) xk .	(3.1)
	max x		k 0
	k

Здесь max xk - наибольшая длина элементарного отрезка.

Операция, приведшая к формуле (3.1) называется интег-

рированием функции на отрезке.

54

	n 1
Сумма:	I f (k ) xk	(3.2)

k 0

называется интегральной суммой для функции f(x) при данном разбиении отрезка a, b на частичные и данном выборе промежуточных точек k .

Интегральных сумм для данной функции и данного отрезка можно составить бесконечно много, так как они зависят от способа разбиения отрезка a, b и от выбора точек k .

Если частичные отрезки становятся сколь угодно мелкими, т.е. max xk 0 , а число n элементарных отрезков в раз-

биении стремиться к бесконечности, то интегральная сумма будет каким-то образом изменяться.

Определение. Если существует предел интегральной суммы (3.2) при max xk 0 и если этот предел не зависит ни от способа разбиения отрезка на частичные, ни от выбора промежуточных точек k , то этот предел называется определен-

ным интегралом от функции f(x) на отрезке a, b и обознача- b

ется: f (x)dx .

a

Здесь а – нижний предел интегрирования, b – верхний предел интегрирования. Таким образом, определенный интеграл - это число, записываемое в виде

b				n 1
	f (x)dx	lim			f (k ) xk .	(3.3)
a		max xk 0		k 0
Геометрический		смысл	определённого интеграла			при

f (x) 0 : определённый интеграл от неотрицательной функ-

ции численно равен площади соответствующей криволинейной трапеции.

55

3.2. Свойства определенного интеграла

Из определения вытекают следующие свойства.

	b
1.	dx b a .
	a
	b	b	a
2.	f (x)dx f (x)dx , а если a=b, то		f (x)dx 0 .
	a	a	a	a, b , интегри-
3.	Функция f(x) непрерывная на отрезке

руема на этом отрезке.

4. Постоянный множитель можно выносить за знак определённого интеграла

b	b
Af (x)dx A f (x)dx .
a	a

5. Если функции f(x) и g(x) интегрируемы на a, b , то оп-

ределённый интеграл их алгебраической суммы равен алгебраической сумме интегралов от слагаемых

b b b

f (x) g(x) dx f (x)dx g(x)dx .

a a a

Замечание. Свойство справедливо для любого конечного числа слагаемых.

6. Если отрезок a, b разбит точкой с на части, то инте-

грал по всему промежутку равен сумме интегралов по его частям (при любом расположении точек a, b, и с).

b c b

f (x)dx f (x)dx f (x)dx .

a a c

56

a<b).

a

7. Если функция f (x) 0		интегрируема на отрезке a, b
	b
(a<b), то	f (x)dx 0 .
	a		a, b (a<b) и
8. Если f(x) и g(x) интегрируемы на отрезке
удовлетворяют на нём равенству f (x) g(x) , то
b	b

f (x)dx g(x)dx (неравенства можно интегрировать, когда

a

9. Если функция f(x) интегрируема на a, b (a<b) и существуют числа m и М такие, что во всех точках отрезка a, b выполняется неравенство m f (x) M , то

b

m(b a) f (x)dx M (b a) .

a

10. Если функция f(x) непрерывна на отрезке a, b , то внутри отрезка найдется хотя бы одна точка с c a, b такая,

	b
что имеет место равенство:	f (x)dx	f (c)(b a) .
	a

3.3. Вычисление определённого интеграла. Формула Ньютона-Лейбница

Если функция f(x) непрерывна на отрезке a, b и F(x)

есть одна из первообразных для f(x) на a, b , то имеет место формула для вычисления определённого интеграла

b

f (x)dx F (x) ba

a

F(b) F(a)

(3.4)

57

- формула Ньютона – Лейбница.

Примеры. Вычислить определенные интегралы.

		2											x3								2
	1. x2dx																						8					1				7		.
											3										1		3					3				3
		1
		1
							dx																		1
	2.											arctgx													0 arctg1 arctg 0											4 .
				1			x				2
		0
				3															3
							dx				1															1						2
	32.																											1							.
							x2								x				1							3							3
			1
		1															1
						dx					1											1 1 2 . Получили абсурд, так как
	4.																1
						x2								x
1		1
	терпит разрыв																				в точке										х=0, следовательно, применять
x 2

формулу Ньютона-Лейбница нельзя.

3.4. Замена переменной в определённом интеграле

b

Пусть необходимо вычислить f (x)dx , где f(x) – неко-

a

торая непрерывная функция.

Часто для нахождения первообразной приходится вводить новую переменную x (t) . При этом пользуются сле-

дующим правилом:

Теорема. Пусть выполнены следующие условия: 1. Функция f(x) непрерывна на отрезке a, b .

58

2.Функции (t) и (t) непрерывны в промежутке

, и a (t) b при t и

() a;( ) b .

3.Сложная функция f (t) непрерывна на ,

Тогда

b
f (x)dx f (t) (t)dt		(3.5)
a

Замечание. При вычисление неопределённого интеграла с помощью замены переменной в найденной первообразной Φ(t) приходилось возвращаться к старой переменной х. Если

в определённом интеграле наряду с переменной интегрирования заменить и пределы, то надобность возвращения к исходной переменной отпадает.

Примеры.
													t; x t 2
	4										x											2				2
					dx				dx 2tdt														2tdt				t 1		1
1.																									2							dt
	1											0;t1 0										1		t		t 1
						x x1
	0												4;t2					2				0				0
									x2
	2					2				dt														2
																	2
	2 dt													2t			0	2 ln			1 t			0 4 2 ln 3
									t 1
						0
	0
	a													x a sin t							dx a cos tdt
2. a 2						x 2 dx
																			0				x2 a;t2
														x1 0 t1														2
	0
	2																					2
					a 2	a 2 sin 2 ta cos tdt													a 2 cos 2 tdt
	0																					0
																				59