Учебное пособие 1920

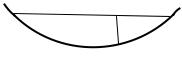
рактеристика будет отделять область, где решение осталось неизменным, от той области, где оно изменилось. Т. е. за всякую характеристическую линию решения уравнения продолжаются неоднозначно.

A M B

Q1 Q

P

Рис. 3.3. Иллюстрация к методу Римана

Предположение, что прямые, параллельные осям, т. е. характеристики, пересекают линию l не более чем в одной точке, будет существенным.

Если не выполнено условие задачи Коши, то она неразрешима.

Пусть кривая l имеет вид, указанный на рис. 3.3. Методом Римана можно вычислить значение функции u(х,у) в точке М (пользуясь криволинейным треугольником PQM, или криволинейным треугольником Q1PM). Полученные две формулы имеют в точке М разные значения для u, т. е. задача Коши будет неразрешимой.

Примеры на приложение метода Римана Пример 1. Найти решение уравнения

x2

д2u

y2

д2u

0,

дx2

дy2

удовлетворяющее условиям

u

y 1

f (x),

дu

F(x).

дy

y 1

y

С помощью замены переменных xy,

приведем

x

уравнение к каноническому виду:

100

	д2u					1			дu		0.
	д д					2 д
		1
	Q	0			, 0						M 0, 0
														1
													,
											P	0		0

Рис. 3.4. Иллюстрация к примеру 1

Прямая у=1 в новых переменных имеет вид равнобочной гиперболы 1 (рис. 3.4).

	При x		,	y		имеем

дu

1 дu 1 дu

дu

2

дu дu

,

д

1

2 дx 2 дy

1

д

1

2

дx

2 дy

1

и

дu

1

1

дu

2

f

F( ),

f

F( ),

д

1

2

2

д

1

2

2

а также u

1

f ( ) .

1

f

0 , тогда

Если в формуле Римана а=0, b

,

2ξ

(uv)P _(uv)Q

1

дu

дv uv

дu

дv

u( , )

(v

u

)d (v

u

)d .

0

0

2

2

д

д

д

д

QP

101

Найдем функцию Римана v( , ; 0; ). Эта функция удовлетворяет сопряженному уравнению

д2v		1 дv
					0
д д		2 д

и условиям на характеристиках:

												d
												2														0
		v( , ; 0, 0 ) e 0																													(на MQ),
		v( , ;									0 d
							0	, ) e 0													1 (на MP).
									0
Функция v( , ; 0 , 0 )													0									это и есть искомая функ-
ция Римана.
Далее					1									1																					1
u(P) f( ), u(Q) f(							), v(P) v( ,												; , ) 1, v(Q) v(																				, ; , ),
											0											0		0																0 0		0
получим					0							0																						0
																									1														1
		f ( 0)																							0				f ( )										0		F( )
						0 0			1										0															0
u( 0, 0)									f (		)																					d										d .
		2					2										4														32			2							32
									0																0														0

Встарых переменным x и y решение задачи Коши:

xx

1

y

x

xy

y

f (z)dz

xy

y

F(z)dz

u(x, y)

f (x, y)

f (

)

.

4

3

2

3

2

2 y

xy

z 2

xy

z 2

Пример 2. Найти решение уравнения

x

д2u

д2u

дu

0(x 0),

дx2

дy2

дx

удовлетворяющее условиям

102

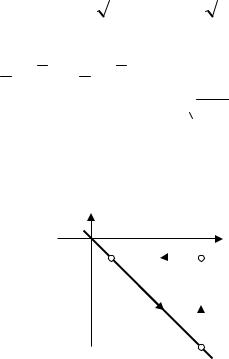
u		y 0	f (x),	дu				F(x).
				дy			y 0

Приведем уравнение к каноническому виду, для чего со-

ставим уравнение характеристик:

xdy2 dx2 0.

Это уравнение имеет два различных интеграла:

	y			C1 ,	y			C 2 .
			x				x
	2				2

Необходимо ввести новые переменные и по форму-

лам y 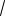x, y x(x 0). Присоединим к этим равен- 2 2

ствам еще одну зависимость w u 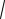, тогда наше уравне-

ние преобразуется к следующему каноническому виду:

	д2w			1 w				0.
				4 ( )2
	д д
A
0		Q 0, 0

B

Рис. 3.5. Кривая AB как биссектриса .

За кривую АВ (рис. 3.5) в методе Римана берем биссектрису . Для решения поставленной задачи найдем част-

103

ное					решение		сопряженного	уравнения
	д2v		1 v			0,
							которое удовлетворяло	бы следующим
			4 ( )2
	д д

условиям на характеристиках:

v( 0, ; 0, 0 ) 1 (на MP);

v( , 0; 0, 0 ) 1 (на MQ).

Решение уравнения ищем в виде v G( ), где

( 0)( 0 ). ( 0 0)( )

Для G( ) получим следующее уравнение:

(1 )G ( ) (1 2 )G ( ) 1G( ) 0. 4

Это уравнение - частный случай гипергеометрического уравнения Гаусса

(1 )y (1 ) y y 0

при 1 , 1. 2

Уравнение Гаусса имеет частное решение в виде гипергеометрического ряда

F( , , , ) 1											( 1) ( 1)								2
																				...,
											2! ( 1)
		1!
абсолютно сходящегося при										1.
Т. е. v G( ) F(	1	,		1	,1; ) 1 (							1	)2 (	1		3		)2 2 ...,
														2
2		2									2				4

Следовательно, функция

v G ( 0)( 0) будет искомой функцией Римана.

( 0 0)( )

Возьмем формулу Римана, и в ней пусть a b 0, f 0.

Тогда

104

w( , )

w(P) w(Q)

1

(v

дw

w

дv

)d (v

дw

w

дv

)d ,

0

0

2

2

д

д

д

д

QP

и

0

w( , )

w(P) w(Q)

1

0 v(

дw

дv

)d

1

w(

дv

дv

)d .

0

0

2

2 0

д

д

2

д

д

0

Вычислим производные. Так как x

1

2, y ,

то

4

дu

дu

дu

дu

дu

дu

.

,

д

дx

дy

y 0

д

дx

дy

y 0

И тогда

дu

дu

2

дu

2F( 2).

д

дy

y 0

д

Дифференцируя w по и и применяя , получим

дw

дu

u

,

дw

дu

u

.

2

2

д

д

2

2

д

д 2

2

Отсюда имеем

дw

дw

(

дu

дu

)

F( 2).

2

2

д

д

д

д

Далее из формул

дv

дG

д

1

( 0)( 0)

(

dG

)

;

д

д д

4

(

) 2

d

дv

дG

д

0

0

dG

1

( 0)( 0)

(

)

д

д д

4

(

) 2

d

0

0

вытекает, что

дv

дv

0

0

(

dG

) .

д

д

2(

) d

0

0

Значение функции w берется на биссектрисе и в точках Р и Q.

105

Так как		w									w( , )																	2 , u(x,0)															2 f ( 2),
получаем
w(P) w( , )																f( 2),w(Q) w( , )																																		f( 2).
												2																																					2
0					0																0													0					0				0								0
Принимая теперь во внимание, что
												u(x , y )															w(				0,		0		)	,
																	0					0							24 x
найдем																																		0
																				f ( 2) f ( 2)
																	0
u(x ,y								0	)																0									0			0
		0
		1												(							)( )
																		0																			2
											G(															0								)F(				)				d
	4																2 (									)
				x																					0
					0			0																		0
										0														0				dG											2				d
														0												(						) f (								)									.
			4(							)4																		d
								0										x			0
											0													0

В старых переменных х и у получим решение задачи Коши:

					y					y2							y					y2										y
																													x
			x		2		f(x	xy		4	)				x		2		f(x	xy		4	)			1		2
u(x,y)																													Ф(x,y,z)dz..
										4															4
												x															x
										2																						y
																													x
																																2

Пример 3. Исследовать процесс передачи тепла в неподвижном горизонтальном слое воды высотой Н=0,01м и начальной температурой T(y,0)=20 C, 0 y H, заключенном между горизонтальными пластинами, на которых поддерживается постоянная температура: на нижней пластине T(0,t)=100 C, на верхней T(Н,t)=20 C, где 0 t tм (рис. 3.6). Рекомендуемое время изучения процесса tм=180 с.

106

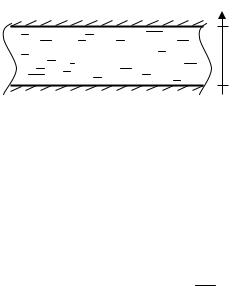
T(H,t)=20 С

T(y,0)=20 С

T(0,t)=100 С

Рис. 3.6. Эскиз слоя воды с исходными данными задачи

	Коэффициент теплопроводности воды				λ 0,59			Дж	;
			Дж			кг		м с К
	теплоемкость	с 4200		; плотность ρ 1000			.
			кг К			м3

Решение. Для численного решения задачи воспользуемся явной разностной схемой Эйлера для уравнения теплопровод-

ности: начальным условием Ti,0=20

C,

i 0,n; граничными

условиями T0,j = 100 C, Tn,j = 20

C,

j

, где h=0,0005 м;

0,m

=0,5 с; коэффициент температуропроводности

a

λ

0,59

14 10 8

м2

;

с ρ

с

4200 1000

n

H

0,01

20;

m

tм

180

360.

0,0005

h

τ

0,5

Для выбранных значений h и условие Куранта

2aτ 2 14 10 8 0,5

0,56 1

h

2

2

0,0005

выполняется, и можно приступать к составлению программы. Текст программы, реализующей вычисления по указанной

схеме в математическом пакете MathCAD, представлен ниже

107

Программа моделирования процесса теплопроводности в неподвижном слое жидкости

по явной разностной схеме Эйлера

Уравнение

d

d2

теплопроводности:

T

a

T

dt

dy2

a 14 10 8

H 0.01 м

n

H

h

h 0.0005 м

n 20

tm 180 с

0.5 с

m

tm

m 360

C

a

2C 0.56

Условие Куранта 2С<1

h2

выполняется

Начальное условие:

i 0

n

Ti 0 20

Граничные

j 0

m

T0 j

100

Tn j 20

условия:

Явная разностная схема Эйлера

F(T)

for j 0

m 1

for i 1

n 1

Ti j 1 (1 2C) Ti j C Ti 1 j Ti 1 j

T

Результаты решения представлены на рис. 3.7, иллюстрирующем различные временны' е сечения процесса.

108

	100
T
i 0	75
T
i 20
T
i 120	50
T
i 240
T	25
i 360
	0	10	20
	0
		i

Рис. 3.7. Изменение температуры слоя жидкости в слое в моменты времени 0,20,120,240,360 с

На рис. 3.7 показано распределение температуры в подогреваемом слое в моменты времени 0, 15, 60, 120 и 180 с.

Координата y представлена номерами i узлов сетки и изменяется от 0 до 20; аналогично по оси времени номера узлов изменяются от 0 до 360.

Рисунок показывает, что по истечении 180 с процесс нагревания жидкости практически завершается и в слое устанавливается линейное распределение температуры: от 100 С у нижней границы до 20 С у верхней.

4. ЗАДАЧИ ЭЛЕКТРОТЕХНИКИ

4.1. Дифференциальные уравнения свободных электрических колебаний

Если по проводу пропускают электрический ток, то образуется электромагнитное поле, которое изменяет силу тока и величину напряжения. В проводе появляется колебательный процесс.

Пусть ось Ох направлена по оси провода, начало коорди-

109