
5532
.pdf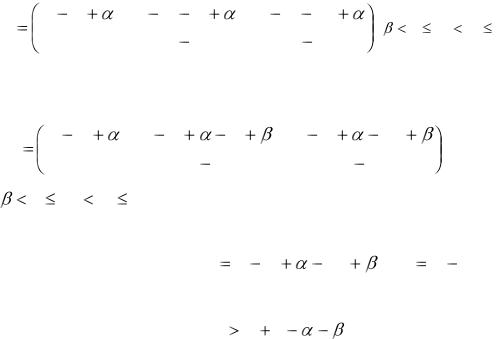
102
мещает страхователю сумму L, а цессионер возмещает цеденту сумму S1-S0. Будем предполагать, что имеет место франшиза β, причём β = К1S, где S — страховая сумма, и
договор перестрахования предполагает комиссию α, где α=KR, R — перестраховочная премия.
Как и выше, страховую премию по оригинальному договору страхования будем обозначать величиной P. Согласно определению договора перестрахования эксцедента сумм, возможны три различные ситуации: S≤S0, S0<S<S1, S1<S. Следовательно, необхо-
димо рассмотреть три случая.
Первый случай: S≤S0. Наступивший убыток компенсируется прямым страховщи-
ком и, следовательно, перестрахования нет.
Второй случай: S0<S≤S1.
Определим матрицу последствий Q. Будем рассматривать задачу принятия решения цедентом. Решений здесь также два: i=1 соответствует принятию решения о передаче риска в перестрахование, i=2 соответствует отказу от передачи риска в перестрахование.
Ситуаций во внешней финансовой среде будет три: j=1 соответствует ситуация ненаступления страхового случая или наступления страхового случая с ущербом L0 ≤ β; j = 2 соответствует ситуации наступления страхового случая с ущербом β<L≤S0; j=3 со-
ответствует ситуации наступления страхового случая с ущербом S0<L1≤S. Тогда элементы матрицы Q находятся из формул: q11= P-R+α, q12=P-R-L+α, q13=P-R-S0+α, q21=P, q22=P-L, q23=P-L1. Матрица Q принимает вид:
Q |
P |
R |
P |
R |
L |
P |
R |
S0 |
, |
|
L |
S0 |
L1 S . (41) |
|
|
P |
|
P |
L |
|
|
P |
L1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
Матрица Q построена для условной франшизы. Для безусловной франшизы мат- |
||||||||||||||
рица последствий Q1 имеет вид: |
|
|
|
|
|
|
|
|
|
|
||||
Q1 |
P |
R |
P |
R |
|
L |
|
P |
R |
S0 |
|
, |
(42) |
|
|
P |
|
P L |
|
|
|
P |
L1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
L S0 L1 |
S . |
|
|
|
|
|
|
|
|
|
|
|
|
Применим правило Вальда для матрицы (42). Для этого найдём минимальные элемен- |
||||||||||||||
ты q1 и q2 первой и второй строк: |
q |
P |
R |
|
S0 |
, |
q |
2 |
P |
L1 . Для выбора |
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
максимального элемента из двух q1 и q2 решим неравенство q1 > q2. Решение имеет вид: |
||||||||||||||
|
|
|
|
|
L1 |
S 0 |
R |
|
. |
|
|
|
|
(43) |
Таким образом, получаем следующий вывод:

103
–при выполнениинеравенства(43)следует принятьрешениеопередачерискавперестрахование;
–при выполнении неравенства
L1 S0 R |
(44) |
следует принять решение об отказе в передачи риска в перестрахование. Неравенства
(43) и (44) опять содержат случайную величину L1. Тем не менее, пользуясь ограниче-
ниями на параметры перестраховочного договора, можно получить детерминистские варианты условий принятия решений. Так, например, если выполняется неравенство
R |
0 , |
(45) |
то неравенство (43) выполняется при любых значениях ущерба L1, так как выполняется |
||
условие L1>S0. Неравенство (45) в терминах относительных величин имеет вид |
|
|
r 1 K T |
K1. |
(46) |
Отсюда следует вывод: при выполнении неравенства (46) следует передать риск в перестрахование. Неравенство (46) содержит основные показатели перестраховочного договора. В отличие от квотно-пропорционального перестрахования, в условии (46)
присутствует и перестраховочная квота r (в части премии). При задании трёх показате-
лей четвёртый находится из условия (46). Тариф по оригинальному договору известен.
Если при этом задать процент комиссии K и коэффициент франшизы, то из (46) можно
выбрать квоту r. Если теперь предположить выполнение неравенства |
|
||||
|
S |
S0 R |
, |
(47) |
|
то неравенство (44) выполняется при любых значениях L1, так как по условию задачи |
|||||
L1≤ S. В терминах относительных показателей неравенство (47) имеет вид: |
|
||||
1 |
|
S0 |
rT 1 K |
K1 . |
(48) |
|
S |
||||
|
|
|
|
|
|
Отсюда следует вывод:
–при выполнении неравенства (46) следует принять решение о передаче риска в перестрахование;
–при выполнении неравенства (48) следует принять решение об отказе в передаче риска в перестрахование.
Если выйти из условий полной неопределённости в части убыточности страховой
суммы, то условия (43) и (44) принятия решений имеют вид: |
|
|
– при выполнении неравенств |
S0 / S rT 1 K K1 , |
S0 / S следует при- |
нять решение о передаче риска в перестрахование; |
|
|
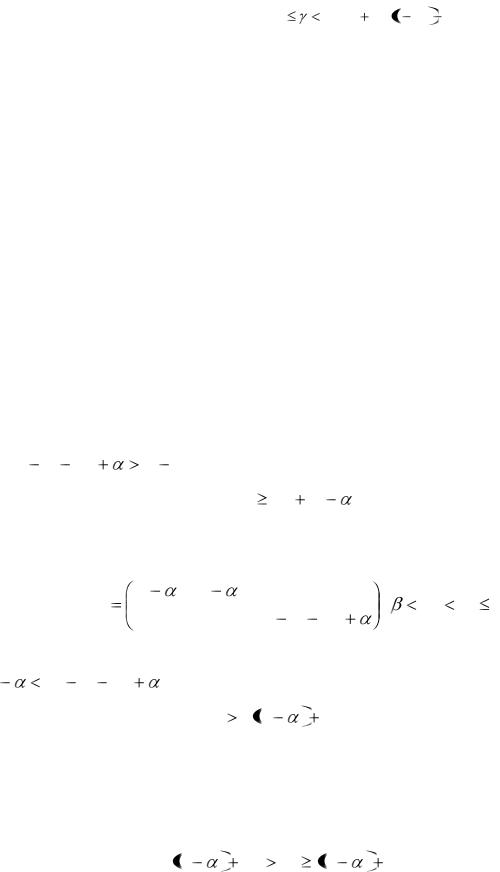
104 |
|
– при выполнении неравенства S0 / S |
S0 / S rT 1 K K1 следует принять |
решение об отказе в передаче риска в перестрахование.
На основании применения правила Вальда можно сделать ряд выводов:
1.Для безусловной франшизы найдены частные детерминистские условия принятия решений.
2.При наличии статистики убыточности страховой суммы найдены общие детер-
министские условия принятия решений.
3. Правило Вальда в задаче принятия решения о перестраховании и при квотно-
пропорциональном перестраховании и при эксцеденте сумм перестрахования даёт спо-
соб принятия решения, если фактически ориентироваться на наступление страхового случая, так как наихудшим состоянием при каждом решении является наступление
страхового события.
Проведём анализ принятия решения о перестраховании на основании критерия Сэвиджа. Построим матрицу рисков для матрицы последствий (41) (условная франши-
за). Максимальные элементы ωj, j=1,2 по первым двум столбцам определяются равен-
ствами ω1=Р, |
ω2=P-L. |
Для определения |
ω3 |
необходимо решить |
неравен- |
ство P R S0 |
P |
L1 . Решение имеет вид: |
|
|
|
|
|
L1 S0 |
R |
. |
(49) |
Таким образом, необходимо рассмотреть два варианта. |
|
||||
1. Пусть выполняется неравенство (49). Тогда матрица рисков имеет вид: |
|
||||
|
B |
R |
|
R |
|
0 |
, |
S0 L1 |
S . |
|
|
0 |
0 |
L1 |
R S0 |
||||
|
|
|
|
|
|
||||
Для |
принятия |
|
решения |
необходимо |
|
решить |
неравенство |
||
R |
L1 R S0 |
|
|
. Решение имеет вид: |
|
|
|
||
|
|
|
|
L1 |
2 R |
S0 . |
|
|
(50) |
На основании неравенства можно сделать следующий вывод:
–при выполнении неравенства (50) следует принять решение о передаче риска в перестрахование;
–при выполнении неравенства
2 R |
S0 L1 R |
S0 |
(51) |
следует принять решение об отказе в передаче риска в перестрахование.
2. Пусть выполняется неравенство

|
|
|
105 |
|
|
|
|
|
|
L1 |
S0 |
R |
. |
|
(52) |
Тогда матрица рисков имеет вид: |
|
|
|
|
|
||
 |
R |
R |
L1 |
R |
S0 |
, |
S 0 L1 S . |
0 |
0 |
|
0 |
|
|||
|
|
|
|
|
|||
Для принятия решения необходимо решить неравенство |
|
||||||
|
|
max R |
, L1 |
R |
S0 |
|
0 . |
Это неравенство следует из неравенства R>α и L1>S0.
Отсюда следует вывод: при выполнении условия (52)следует принять решение об
отказе в передаче риска в перестрахование.
Объединяя неравенства (51) и (52), можно сделать следующий вывод:
– при выполнении условия (52) следует принять решение о передаче риска в перестрахование;
– при выполнении условия L1 2 R 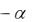
 S0 следует принять решение об отка-
S0 следует принять решение об отка-
зе в передаче риска в перестрахование.
Аналогично можно получить детерминистский вариант условий принятия реше-
ний: при выполнении неравенства 1 S0 / S 2Tr 1 K  следует принять решение об от-
следует принять решение об от-
казе в передаче риска в перестрахование.
Если выйти из условий полной неопределённости, то стохастические условия
можно также заменить детерминистскими: |
|
|
|
|
– при выполнении условия |
S0 / S |
2Tr 1 |
K |
следует принять решение о пере- |
даче риска в перестрахование; |
|
|
|
|
– при выполнении условия |
S0 / S |
2Tr 1 |
K |
следует принять решение об от- |
казе в передаче риска в перестрахование.
Применим к исследованию задачи критерий Гурвица. Рассмотрим вначале условную франшизу и матрицу (41). В первой строке максимальный элемент равен P-R+α, минимальный элемент – величине P-R-S0+α. Во второй строке максимальный элемент равен величине Р, минимальный – величине Р-L1. Для принятия решения необходимо
найти максимальный из двух элементов |
1 |
P |
R S0 |
1 |
P R |
, |
||||
2 |
P L1 1 |
P. |
|
|
|
|
|
|
|
|
|
Решая неравенство ω1>ω2, получим: |
|
|
|
|
|
|
|
|
|
|
|
L |
S |
|
1 |
R |
. |
|
|
(53) |
|
|
0 |
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
Отсюда, согласно критерию Гурвица, можно сделать следующий вывод:
– при выполнении неравенства (53) следует принять решение о передаче риска в

|
|
106 |
|
|
|
перестрахование; |
|
|
|
|
|
– при выполнении неравенства |
L |
S |
0 |
1 R |
следует принять решение об |
|
1 |
|
|
|
|
отказе в передачи риска в перестрахование.
В детерминистском варианте этот вывод формулируется следующим образом: при выполнении неравенства 1 S0 / S 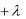 1Tr 1 K
1Tr 1 K 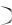 следует принять решение об отказе в
следует принять решение об отказе в
передаче риска в перестрахование.
В условиях частичной неопределённости соответственно имеем:
– при выполнении неравенства |
S0 / S |
1Tr 1 |
K |
следует принять решение о |
передаче риска в перестрахование; |
|
|
|
|
– при выполнении неравенства |
S0 / S |
1Tr 1 |
K |
следует принять решение об |
отказе в передаче риска в перестрахование.
Третий случай: S1<S.
Построим матрицу последствий при принятии решения цедентом. Решение будет,
как и выше, два: i=1, 2. Ситуаций во внешней финансовой среде будет четыре: j=1 со-
ответствует ситуации наступления страхового случая с ущербом L0 ≤ β; j=2 соответ-
ствует ситуации наступления страхового случая с ущербом β<L≤S0; j=3 соответствует ситуации наступления страхового случая с ущербом S0<L1≤S1; j=4 соответствует ситуа-
ции наступления страхового случая с ущербом S1<L2. Тогда элементы матрицы послед-
ствий Q при безусловной франшизе находятся из формул:
q11=P-R+α; q12=P-R+α-L+β; q13=P-R+α-S0+β; q14=P-R+α+β-L2-S0+S1; q21=P; q22=P-L; q23=P-L1; q24=P-L2.
Матрица Q принимает вид:
Q |
P R |
P R |
L |
P R |
S0 |
P R |
L2 S0 |
S1 |
, (54) |
P |
P |
L |
P |
L1 |
|
P L2 |
|
||
|
|
|
|
|
L S0 |
L1 S1 |
L2 |
S . |
|
|
|
|
|
|
При условной франшизе матрица последствий имеет вид: |
|
|
|
|||||
Q1 |
P R |
P R |
|
L P R |
S0 P R |
L2 S0 |
S1 |
, |
(55) |
P |
P |
L |
P |
L1 |
P L2 |
|
|||
|
|
|
|
||||||
L S0 L1 S1 L2 S .
Применим правило Вальда для матрицы (54). Для этого найдём минимальные элементы q1 и q2 первой и второй строк. На основании неравенства (54) q1 P R 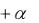
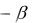 L2 S0 S1 , q2 P L2 .
L2 S0 S1 , q2 P L2 .
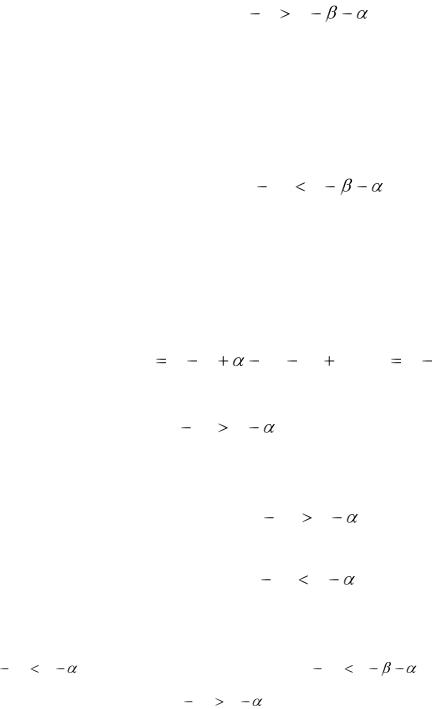
107 |
|
|
Для выбора максимального элемента из двух q1 |
и q2 |
решим неравенство q1>q2. |
Решение имеет вид: |
|
|
S1 S 0 R |
. |
(56) |
Неравенство (56) содержит основные показатели перестраховочного договора и носит детерминистский характер, то есть не содержит случайных величин-ущербов.
Следовательно, на основании критерия Вальда можно сделать обоснованный вывод:
– при выполнении неравенства (56) следует принять решение о передаче риска в
перестрахование; |
|
– при выполнении неравенства S1 S0 R |
следует принять решение об |
отказе в принятии риска в перестрахование.
Таким образом, неравенство (56) может служить основой для переговорного про-
цесса между цедентом и цессионером.
Рассмотрим теперь условную франшизу и матрицу (55). Аналогичным образом
найдём минимальные элементы q1 |
и q2 первой и второй строк матрицы (55) на основа- |
||||||||
нии неравенства (55): q |
P |
R |
|
L2 S0 |
S1 , q |
2 |
P L2 . |
||
|
1 |
|
|
|
|
|
|
|
|
Для выбора максимального элемента из q1 |
и q2 |
решим неравенство q1 > q2. |
|||||||
Решение имеет вид: S1 |
S0 |
R |
. |
|
|
|
|
||
Таким образом, на основании критерия Вальда в случае условной франшизы |
|||||||||
можно сделать вывод: |
|
|
|
|
|
|
|
|
|
– при выполнении неравенства S1 |
S0 |
R |
следует принять решение о пе- |
||||||
редаче риска в перестрахование; |
|
|
|
|
|
|
|||
– при выполнении неравенства S1 |
S0 |
R |
следует принять решение об от- |
||||||
казе в передаче риска в перестрахование. |
|
|
|
|
|
||||
Отметим |
здесь, что |
в |
практике |
перестраховочных |
договоров соотношение |
||||
S1 S0 R |
, как впрочем, и соотношение S1 |
S0 |
R |
|
реализуется значитель- |
||||
но реже, чем неравенство S1 |
S0 |
R |
или (56). Это объясняется тем, что величины |
||||||
собственного удержания цедента и предела ответственности цессионера имеют порядок страховых сумм, в то время как правая часть, например, неравенства (56) имеет поря-
док страхового тарифа. Отсюда следует, что правило Вальда рекомендует скорее реше-
ние о передаче риска в перестрахование, чем отказ от перестрахования. Применим те-
перь к проблеме принятия финансового решения о передаче риска в перестрахование критерий Сэвиджа минимизации риска упущенной выгоды для случая условной фран-

108
шизы. Построим матрицу рисков на основании матрицы финансовых последствий.
Максимальный элемент первого столбца ω1=Р, второго столбца ω2=Р-L. Макси-
мальный элемент ω3=Р-L1 при условии |
L1 |
S0 |
R |
|
. Максимальный |
элемент |
||||||
ω4=Р-L2 при условии S1 |
S0 |
R |
. |
|
|
|
|
|
|
|
|
|
Для дальнейшего анализа необходимо рассмотреть четыре случая. |
|
|
|
|||||||||
1. Пусть выполняется система неравенств |
|
|
|
|
|
|
|
|||||
|
|
L1 |
S0 |
R |
, |
S1 |
S0 |
R |
. |
|
|
(57) |
Тогда матрица рисков имеет вид: |
|
|
|
|
|
|
|
|
|
|||
B |
R |
R |
|
R |
|
S0 |
L1 |
R |
S0 |
S1 |
. |
|
0 |
|
0 |
|
|
0 |
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
||||
Максимальный элемент δ1 первой строки этой матрицы, ввиду условий, (57) определя-
ется равенством 1 R  . Так как δ1>0, то следует принять решение об отказе в передаче риска в перестрахование. Учитывая тот факт, что первое неравенство системы (57) является следствием второго неравенства, можно сделать следующий вывод. Согласно правилу Сэви-
. Так как δ1>0, то следует принять решение об отказе в передаче риска в перестрахование. Учитывая тот факт, что первое неравенство системы (57) является следствием второго неравенства, можно сделать следующий вывод. Согласно правилу Сэви-
джа, для условной франшизы при выполнении второго неравенства системы (57) следует принять решение об отказе в передаче риска в перестрахование.
2. Пусть выполняется система неравенств
L1 S0 R , S1 S0 R . |
(58) |
Тогда матрица рисков имеет вид:
B |
R |
R |
R |
S0 |
L1 |
|
0 |
|
. |
0 |
0 |
|
0 |
R |
|
S0 |
S1 |
||
|
|
|
|
||||||
Максимальный элемент δ1 |
первой строки определяется равенством δ1=R-α, второй |
||||||||
строки – равенством 2 |
R |
S0 S1 . Для принятия оптимального решения необ- |
|||||||
ходимо решить неравенство δ1<δ2. Решение имеет вид S1 |
S0 |
2 R |
|
. |
|||||
Отсюда на основании критерия Сэвиджа можно сделать следующий вывод: |
|||||||||
– при выполнении неравенства S1 |
S0 |
2 R |
и системы (58) следует при- |
||||||
нять решение о передаче риска в перестрахование; |
|
|
|
|
|||||
– при выполнении системы (58) и неравенства S1 |
S0 |
2 R |
|
следует при- |
|||||
нять решение об отказе в передаче риска в перестрахование. |
|
|
|
||||||
3. Пусть выполняется система неравенств L1 S0 R |
, |
S1 S0 |
2 R |
. |
|||||
Ввиду неравенства S1 ≥ L1 |
постановки задачи, эта система неразрешима. Следова- |
||||||||

109
тельно, такой вариант не реализуется.
|
4. Пусть выполняется система неравенств L1 |
S0 |
R |
, |
S1 |
S0 2 R |
. |
|||||||
|
Тогда матрица имеет вид: |
|
|
|
|
|
|
|
|
|
||||
|
|
B |
R |
R |
|
|
0 |
|
|
|
|
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
0 |
R |
|
S0 |
L1 |
R |
|
S0 S1 |
||
|
Максимальный |
элемент |
первой строки |
δ1=R-α, |
второй |
строки |
– элемент |
|||||||
2 |
R |
S0 S1 . |
Для принятия оптимального решения необходимо решить нера- |
|||||||||||
венство δ1<δ2. Решение имеет вид S1 |
S0 |
2 R |
|
. |
|
|
|
|
||||||
|
На основании вышеизложенного можно сделать следующий вывод: |
|
||||||||||||
|
– при выполнении данной системы и неравенства |
S1 |
S0 |
2 R |
следует |
|||||||||
принять решение о передаче риска в перестрахование; |
|
|
|
|
|
|||||||||
|
– при выполнении данной системы и неравенства S1 |
S0 |
2 R |
следует принять |
||||||||||
решение об отказе в передаче риска, в перестрахование. Объединяя варианты |
1 – 4, можно |
|||||||||||||
сделать следующий вывод. На основании критерия Сэвиджа для условной франшизы: |
||||||||||||||
|
– при выполнении неравенства |
S1 |
S0 |
2 R |
|
следует принять решение о |
||||||||
передаче риска в перестрахование; |
|
|
|
|
|
|
|
|
|
|||||
|
– при выполнении неравенства S1 |
S0 |
2 R |
|
следует принять решение об |
|||||||||
отказе в передаче риска в перестрахование. |
|
|
|
|
|
|
|
|||||||
|
Таким образом, в случае условной франшизы критерий Сэвиджа также предлагает |
|||||||||||||
детерминистский инструмент принятия решения. Отметим, также, что при выполнении условия S1 S0 2 R 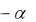
 (условная франшиза) оба критерия Вальда и Сэвиджа ука-
(условная франшиза) оба критерия Вальда и Сэвиджа ука-
зывают на принятие решения о передачи риска в перестрахование. При выполнении неравенства S1 S0 2 R 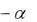
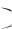 (условная франшиза) оба критерия Вальда и Сэвиджа указывают на принятие решения об отказе в передаче риска в перестрахование.
(условная франшиза) оба критерия Вальда и Сэвиджа указывают на принятие решения об отказе в передаче риска в перестрахование.
Применим теперь к задаче критерий Гурвица. Рассмотрим случай безусловной фран-
шизы (матрица финансовых последствий (54)). Максимальный элемент перовой строки, в
силу условий (54), равен величине P-R+α. Аналогично минимальный элемент равен вели-
чине P R 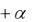
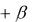 L2 S0 S1 . Следовательно, для первой строки средневзвешен-
L2 S0 S1 . Следовательно, для первой строки средневзвешен-
ное значение ω1 между наибольшим и наименьшим элементами определяется равенством
1 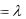 P R
P R 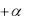
 L2 S0 S1
L2 S0 S1 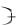 1
1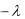 P R
P R 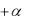 .
.

|
|
|
110 |
|
|
|
|
||
Аналогичным образом можно найти |
|
|
1 |
P |
L2 |
1 |
P P L2 . |
||
Для принятия оптимального решения необходимо решить неравенство ω1>ω2. Ре- |
|||||||||
шение имеет вид S S |
1 R |
. |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
Отсюда на основании критерия Гурвица для безусловной франшизы можно сде- |
|||||||||
лать следующий вывод: |
|
|
|
|
|
|
|
|
|
– при выполнении неравенства |
S |
S |
0 |
|
1 R |
|
следует принять решение о |
||
|
|
1 |
|
|
|
|
|
|
|
передаче риска в перестрахование; |
|
|
|
|
|
|
|
|
|
– при выполнении неравенства |
S |
S |
0 |
1 |
R |
|
следует принять решение |
||
|
|
1 |
|
|
|
|
|
|
|
об отказе в передачи риска в перестрахование.
Здесь можно отметить, что при λ=1 критерий Гурвица и Вальда дают одинаковый результат. Это следует из теории принятия статистических решений. При условии
λ=1/2 критерии Гурвица и Сэвиджа дают одинаковый результат. Значение λ=1/2 соот-
ветствует тому, что оптимизируется среднее арифметическое между наилучшим и наихудшим результатами по каждому решению. Если цедент выбирает значение λ<1/2,
то это означает, что он склоняется к более оптимистическому для себя развитию ситуа-
ции (ненаступление страхового случая). Такой подход к определению параметра λ мо-
тивирован оценкой вероятностей различных событий: вероятность ненаступления стра-
хового события существенно больше, чем вероятности иных рассматриваемых собы-
тий.
Отметим также, что в случае, когда страховая сумма по договору страхования превосходит предел ответственности цессионера (S>S1) все три критерия Вальда, Сэви-
джа и Гурвица для всех типов франшизы представляют детерминистский результат в задаче о принятии финансового решения о передаче риска в перестрахование.
3.3Моделирование принятия решения о перестраховании
вусловиях частичной неопределённости
Условия частичной неопределённости отличаются от условий полной неопреде-
лённости, как известно, наличием статистической информации. В частности, подразу-
мевается наличие вероятностных характеристик или вероятностей наступления иссле-
дуемых событий. Страховая группа в системе ФПГ при перестраховании рисков нахо-
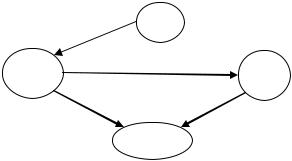
дится как в условиях полной, так и в условиях частичной неопределённости в качестве и цедента, и цессионера. На рисунке 25 изображено перераспределение рисков про-
111
мышленной группы (ПС) через страховую организацию (СОСГ) и перестраховочную организацию (Ре СГ) страховой группы в условиях частичной неопределённости.
В данном случае страховая группа, находясь в системе ФПГ, имеет полную стати-
стическую информацию о распределении рисков ПГ. При этом страховая организация выступает в качестве цедента, проводя первичное перераспределение рисков в пере-
страховочную организацию СГ и страховые организации внешней финансовой среды
(СОВФС). Перестраховочная организация СГ выступает в качестве и цессионера, полу-
чая риски от СОСГ и цедента, проводя вторичное перераспределение рисков в СОВФС.
ПГ
СОСГ |
РеСГ |
СОВФС
Рисунок 25 – Перераспределение рисков в условиях частичной неопределённости
Как было показано в предыдущих разделах, кэптивные страховые организации могут развиваться наиболее эффективно, привлекая страховые финансовые ресурсы из внешней среды, то есть превращаясь, по сути, в универсальные страховые организации. Однако при этом они попадают в условия полной неопределённости, участвуя в системе вторичного перераспределения рисков. На рисунке 26 изображено перераспределение рисков ВФС в системе страховой группы ФПГ в условиях полной неопределённости. При этом и СОСГ, и Ре СГ выступают и как цеденты, и как цессионеры. Вместе с тем следует отметить, что условия полной неопределённости для элементов СГ несколько различаются. Получая риски в качестве цессионеров от перестраховщиков внешней финансовой среды, СГ находится в условиях, когда предыстория полученных рисков в значительной степени теряется. Перераспределяя риски, непосредственно полученные от страхователей ВФС, как СОСГ, так и Ре СГ имеют возможность получить некоторую дополнительную статистическую информацию, например убыточность страховой суммы. Как было показано в подразделах 3.1 и 3.2, даже этой информации достаточно, чтобы получить детерминистские выводы о принятии того или иного финансового решения. Таким образом, в системе управления рисками ФПГ страховая группа находится в условиях частичной неопределённости. В системе поддержания
