Методы вычислительной математики

m
∑ak ϕk (xi )= f (xi ), i =			(4.3)
	0,m
k=0
относительно неизвестных коэффициентов разложения ak ,			k =		.
				1,m

Для существования единственного решения системы алгебраических уравнений (4.3) требуется, чтобы главный определитель этой системы

	ϕ0 (x0 )	ϕ1 (x0 ) … ϕm (x0 )
=	ϕ0 (x1 )	ϕ1 (x1 ) … ϕm (x1 )
	…	… … …
	ϕ0 (xm ) ϕ1 (xm ) … ϕm (xm )
был отличен от нуля, ≠ 0 .

4.1. Интерполяция степенными функциями

Пусть в качестве системы функций ϕk (x) рассматриваются полиномы

ϕk (x)= xk , k = 0,m .

В этом случае принимает вид определителя Вандермонда1:

	1	x0	x02	x03	x0m
	1	x	x2	x3	xm	= ∏(xi − xk ),
=		1	1	1	1
	… … … … … …					i>k
	1	xm	xm2	xm3	xmm
причем ≠ 0 , если среди множества точек xk ,						k =		, нет совпадающих. При
							0,m

m

этом алгебраический интерполяционный многочлен Pn (x) = ∑ak xk всегда су-

k=0

ществует и определен единственным образом.

4.1.1. Интерполяционный полином Ньютона

Для произвольной функции f(x) определяются разделенные разности:

– первая разделенная разность

f (xi , x j )= [f (xi )− f (x j )]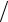(xi − x j ),

– вторая разделенная разность

1 Вандермонд Александр Теофиль [28.2.1735 – 1.1.1796] – французский математик, являлся членом Парижской академии наук с 1771 года.

91

f (xi , x j , xk )= [f (xi , x j )− f (x j , xk )](xi − xk ),

– третья разделенная разность

f (xi , x j , xk , xl )= [f (xi , x j , xk )− f (x j , xk , xl )]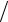(xi − xl ),

и так далее.

Первые разделенные разности f (xi , x j ) и f (x j , xk ) являются разностными

аналогами первых производных функции f(x) на соответствующих отрезках
[xi , x j ]	и	[x j , xk ]. Вторая разделенная разность f (xi , x j , xk ) аппроксимирует

вторую производную функции f(x) на отрезке [xi , xk ]. Соответственно, третья разделенная разность – аналог третьей производной на отрезке [xi , xl ], и так далее. Пусть Pm (x) – искомый интерполяционный многочлен. Разделенные разности для этого полинома имеют вид

Pm (x, x0 )= [Pm (x) − Pm (x0 )]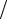(x − x0 ),

Pm (x, x0 , x1 ) = [Pm (x, x0 ) − Pm (x0 , x1 )]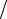(x − x1 ),

Pm (x, x0 , x1, x2 ) = [Pm (x, x0 , x1 )− Pm (x0 , x1, x2 )]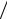(x − x2 ), …

Отсюда получается выражение для полинома в виде

Pm (x)= Pm (x0 )+ (x − x0 )Pm (x, x0 )=

=Pm (x0 )+ (x − x0 )[Pm (x0 , x1 ) + (x − x1 )Pm (x, x0 , x1 )]=

=Pm (x0 )+ (x − x0 )[Pm (x0 , x1 )+ (x − x1 ){Pm (x0 , x1, x2 )+ (x − x2 )Pm (x, x0 , x1, x2 )}]=…

Иначе это выражение можно записать в форме

Pm (x)= Pm (x0 ) + (x − x0 )Pm (x0 , x1 )+

+ (x − x0 )(x − x1 )Pm (x0 , x1, x2 )+ (x − x0 )(x − x1 )(x − x2 )Pm (x, x0 , x1, x2 ) +…

Эта цепочка конечна и содержит m + 1 слагаемое. В самом деле, Pm (x) – полином степени m; разность Pm (x)− Pm (x0 ) при x = x0 обращается в нуль, то есть x0 является корнем выражения Pm (x)− Pm (x0 ), и, следовательно, оно без остатка делится на разность x − x0 . Но в этом случае

Pm (x, x0 )= [Pm (x) − Pm (x0 )]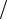(x − x0 )

оказывается полиномом степени m – 1. Соответственно, Pm (x, x0 , x1 ) – полином степени m – 2, и так далее. В итоге Pm (x, x0 ,…, xm−1 ) – полином степени m – m = 0, то есть константа, и наконец, P(x, x0 ,…, xm )= 0 .

В силу условия (4.1) имеет место Pm (xi )= f (xi ), i = 0,m , откуда следует

92

Pm (x)= f (x0 )+ (x − x0 )f (x0 , x1 )+ (x − x0 )(x − x1 )f (x0 , x1, x2 )+…,

либо, в ином виде,

Pm (x)= f (x0 )+ (x − x0 )[f (x0 , x1 )+ (x − x1 ){f (x0 , x1, x2 )+…}].

Пример 4.1. Аппроксимировать функцию sin(x) на отрезке [0, π/2].

В табл. 4.1 приведены значения заданной функции и ее разделенные разности в узлах разностной сетки на указанном отрезке.

				Таблица 4.1
	Таблица интерполяции функции sin(x) по 4 точкам
xi	f (xi )	f (xi , xi+1 )	f (xi , xi+1, xi+2 )	f (xi , xi+1, xi+2 , xi+3 )
0	0
		0,9549297
π/6	0,5		–0,2443404
		0,6990570		–0,1138719
π/3	0,8660254		–0,4232099
		0,2558726
π/2	1,0

Полиномиальная аппроксимация заданной функции имеет вид

sin(x) ≈ 0 + (x − 0)[0,9549297 + (x − π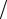6){− 0,2443404 + (x − π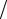3)(− 0,1138719)}].

Для аргумента x = π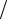4, отсутствующего в табл. 4.1, построенный полином принимает значение, равное 0,705889. Табличное значение этой функции равно sin (π4) = 0,707107. Относительная погрешность вычисления составля-

ет 0,172 %.

Пример 4.2. Определить корень уравнения f (x) = (1 + x)ex2 − 2,5 = 0 мето-

дом обратной интерполяции.

Идея метода обратной интерполяции заключается в построении полинома Ньютона для функции, обратной к заданной зависимости f (x), то есть x( f ). Особенность данного случая – необходимость построения полинома Ньютона для обратной функции x( f ) на сетке с переменным шагом по координате fi . В табл. 4.2 приведены значения заданной функции и ее разделенные разности в узлах разностной сетки на указанном отрезке.

93

				Таблица 4.2
Таблица для построения обратной интерполяции функции x(y)
fi	x( fi )	x( fi , fi+1 )	x( fi , fi+1, fi+2 )	x( fi , fi+1 , fi+2 , fi+3 )
–1,083564	0,25
		0,4905784
–0,5739619	0,50		–0,07743017
		0,4030978		0,013912025
0,04623498	0,75		–0,05126156
		0,3327975
0,7974425	1,0

Интерполяционный полином Ньютона для этой задачи имеет вид x( f ) = 0,25 + ( f +1,08356)[0,49058 +

+ ( f + 0,57396){− 0,07743 + ( f − 0,04624)0,01391}].

Для f = 0 построенный полином принимает значение x(0) = 0,733018. Точное решение x = 0,732941. Относительная погрешность вычисления корня составляет 0,0105 %.

4.1.2. Интерполяционный полином Лагранжа

Интерполяционный полином Лагранжа строится в следующем виде:

m
Lm (x) = ∑ f (xk )ϕk (x),	(4.4)

k=0

то есть в каждой точке x значение полинома Lm (x) определяется как линейная комбинация табличных значений f (xk ), k = 0,m . Условие (4.1) приводит к выражению

m

Lm (xi ) = ∑ f (xk )ϕk (xi )= f (xi ), i = 0,m ,

k=0

которое оказывается справедливым при выполнении условия

0,	i ≠ k,
ϕk (xi )=	i = k.
1,

Это означает, что на отрезке интерполяции [a, b] каждая из функций ϕk (x), k = 0,m , должна иметь m корней. Естественно представить каждую из функций ϕk (x) в виде полинома

94

ϕk (x) = λk (x − x0 )(x − x1 ) … (x − xk−1 )(x − xk+1 ) … (x − xm ),

где λk	– нормировочный коэффициент, определяемый из условия ϕk (xk ) =1,
		λk =1 (xk − x0 )(xk − x1 ) … (xk − xk−1 )(xk − xk+1 ) … (xk − xm ).
Полином Лагранжа можно записать в общем виде:
L		(x) = m	(x − x0 ) … (x − xk−1 )(x − xk+1 ) … (x − xm )	f (x	k	).	(4.5)
m		∑k=0	(xk − x0 ) … (xk − xk−1 )(xk − xk+1 ) … (xk − xm )

4.1.3. Погрешность полинома Ньютона (Лагранжа)

Погрешность представления функции f (x) полиномом Pm (x) или полиномом Lm (x) оценивается разностью

r(x)= f (x) − Pm (x), x [a,b].

Очевидно, что в узлах xk , k = 0,m , погрешность r(xk ) = 0 .

Для оценки погрешности выбирается и фиксируется произвольная точка

x [a, b], x ≠ xk , k =		. Рассматривается вспомогательная функция
	0,m
g(t) = f (t)− Pm (t)− Kω(t), t [a,b],			(4.6)
где ω(t)= (t − x0 )(t − x1 ) … (t − xm ), K – константа. Очевидно, что			g(xk )= 0 ,

k = 0,m. В выражении (4.6) константа K выбирается из расчета, чтобы для вы-

бранной точки x функция g(x) обращалась в ноль, то есть

K = [f (x)− Pm (x)]ω(x).

Пусть функция f (x) имеет m + 1 производную, то есть является достаточ-

но гладкой функцией. Согласно построению функция g(t) имеет не менее m + 2 нулей в точках x, x0 ,…, xm . В этом случае функция gt′(t) на отрезке [a, b] имеет

не менее m + 1 нулей; gtt′′(t) – не менее m нулей, и так далее. И, наконец, gt(…mt+1) (t) имеет хотя бы один корень на отрезке [a, b]. Иначе говоря, ξ [a,b],

gt(…mt+1) (ξ)= 0 . В силу определения функции g(t)

gt(…mt+1) (t)= ft…(mt+1) (t)− K(m +1)!,

и для точки ξ получается

ft…(mt+1) (ξ)= K(m +1)!= [f (x)− Pm (x)](m +1)!ω(x).

Отсюда следует:

f (x) − Pm (x)= ft…(mt+1) (ξ)ω(x)(m +1)!.

Окончательно

f (x)− Pm (x)		≤ M m+1		ω(x)		(m +1)!.	(4.7)

95

Здесь обозначено: M m+1 = sup ft…(mt+1) (t) . В частном случае, когда f (x) яв-

t [a,b]

ляется полиномом степени m, M m+1 = 0 и f (x)≡ Pm (x). Дополнительно можно подобрать такое распределение узловых точек xk , k = 0,m , чтобы минимизиро-

вать выражение

ω(x) = (x − x0 )(x − x1 ) … (x − xm ) = 1xm+1 + αm xm + αm−1xm−1 +…+ α0 ,

являющееся полиномом степени m+1 со старшим коэффициентом, равным 1. Иначе говоря, ставится задача Чебышёва, рассмотренная ранее. Искомый поли-

ном имеет на отрезке [a, b] корни

xn = [(b + a)+ (b − a)cos((2k +1)π2(m +1))]2, k = 0,m .

Оценка модуля полинома, наименее уклоняющего от нуля,

max ω(x) = (b − a)m+1 22m+1 ,

x [a,b]

и оценка погрешности полинома Ньютона (Лагранжа) при использовании узловых точек, соответствующих корням полинома Чебышёва, имеет вид

f − Pm				= max		f (x)− Pm (x)		≤ M m+1 (b − a)m+1	22m+1 (m +1)!
				x [a,b]

4.1.4. Интерполяционный полином Эрмита1

Если заданы не только значения функции f (xk ), но и значения некоторых ее производных в точках xk , k = 0,m отрезка [a, b], то при построении аппроксимирующего полинома необходимо требовать совпадения не только значений

функции (4.1), но и значений производных в указанных точках. В этом случае интерполяция носит название эрмитовой, а сам полином обозначается H p (x).

Для определения вида H p (x) первоначально строится полином Ньютона Pm (x). Далее производится сближение узлов, например, x0 и x1 , которые в пределе

сливаются, то есть появляется кратный узел x0 ≡ x1 , что делает невозможным
подсчет разделенной разности		f (x0 , x1 ) = [f (x0 ) − f (x1 )] (x0 − x1 ). Однако пре-
дельный переход позволяет определить, что
lim f (x0	, x1 )= lim	( f (x0 )− f (x1 )) (x0 − x1 )= fx′(x0 ).
x1→x0	x1→x0

Иными словами, первая разделенная разность, что уже отмечалось ранее,

впределе совпадает со значением первой производной в точке x0 . Это будет

1Эрмит Шарль [24.12.1822 – 14.1.1901] – французский математик. С 1856 года являлся членом Парижской академии наук, с 1857 года – иностранным членом-корреспондентом Петербургской академии наук. С 1869 года был профессором Парижского университета. С1873 года стал членом Лондонского королевского общества. С 1895 года избран иностранным почетным членом Петербургской академии наук.

96

означать также, что полином Эрмита H p (x) позволяет правильно передавать

значения производных. Разделенные разности более высоких порядков определяются с учетом этого следующим образом:

f (x0 , x0 , x1 )= [fx′(x0 )− f (x0 , x1 )](x0 − x1 ),

f (x0 , x0	, x1, x1 ) =[f (x0 , x0 , x0 )− f (x0 , x1, x1 )] (x0 − x1 ) =
=	[fx′(x0 )− 2 f (x0 , x1 ) + fx′(x1 )] (x0 − x1 ).
Отсюда следует, что слияние трех узлов дает возможность интерполяции зна-
ченийвторыхпроизводных, итакдалее. Вобщемслучае имеетместо формула
				(m−1)
		, x0 ,…, x0			(x0 ) (m −1)!.
	f x0			= fx…x
		m

Оценка точности аппроксимации полинома Эрмита выполняется с ипользованием формулы (4.7):

f (x)− H p (x)

(p +1)!,

p

p

≤ M p+1

~

~

mk

,

∑mk = p +1,

ω(x)

ω(x)=

∏(x − xk )

где p – число точек интерполяции, mk

k=0

k=0

– число значений функции и ее произ-

~

обеспечивает обращение

водных в точке xk . Указанный выбор функции ω(x)

в нуль не только g(x), но и ее производных gxm…k

x (xk ). На рис. 4.1 приведены при-

ближения функции f (x) = x + sin(x) полиномами Эрмита H3(x), H5(x), H7(x) и H9(x)

(последний полином практически сливается с самой функцией) и полиномом Лагранжа L9(x) для отрезка [0, 25] на равномерных сеточных множествах.

Рис. 4.1. Полиномы Эрмита и Лагранжа для функции x + sin(x)

4.1.5. Сходимость процесса интерполяции полиномами

97

Множество точек a ≤ x0 < x1 <…< xm ≤ b называется сеткой на отрезке [a,b] и обозначается Ωm . Рассматривается последовательность Ω0 ,Ω1,Ω2 ,… сеток, определенных на этом отрезке. На отрезке [a,b] строится последовательность полиномов Pm (x), аппроксимирующих с помощью сеток Ωm заданную функцию f (x).

Интерполяционный процесс сходится в точке x* [a,b], если существует

предел lim P (x* )= f (x* ) (определение поточечной сходимости).
m→∞ m
Интерполяционный процесс сходится равномерно на отрезке [a,b], если
f − Pm = max f (x)− Pm (x) →0.
x [a,b]	m→∞

Теорема 4.1 (Фабера1). Какова бы ни была последовательность сеток Ωm , найдется непрерывная на [a,b] функция f (x) такая, что последовательность интерполяционных полиномов Pm (x) не сходится к f (x) равномерно на этом отрезке.

На рис. 4.2 приведен пример аппроксимации функции f (x)= x на отрезке [−1,1] с использованием последовательности сеток с равноотстоящими узлами.

Рис. 4.2. Полиномы Pm для функции x на равномерных сетках

Нарис. 4.3 представлена погрешность аппроксимации функции f (x)= x полиномамиPm наравномерныхсеткахвзависимостиотчислаотрезковсеточнойобласти.

1 Фабер Георг [5.4.1877 – 1966] – немецкий математик, был профессором Высшей технической школы в Мюнхене с 1916 года.

98

	||f –P m ||
	1E+11
	1E+07
	1000
	0,1
	2	4	8	16	32	64
	Рис. 4.3. Погрешность аппроксимации функции f (x)= x
		полиномами Pm на равномерных сетках
Теорема 4.2. Если функция			f (x) непрерывна на отрезке [a,b], то найдется
такая последовательность сеток, для которой интерполяционный процесс схо-
дится равномерно на этом отрезке.
На	рис. 4.4	приведен пример		аппроксимации непрерывной функции
f (x)= x	полиномами на последовательности неравномерных (чебышёвских)
сеток.
	1,4
	1,2
	1,0
	0,8
	0,6	P 8			P 4	P 2
	0,4		P 16
	0,2			| x |
	0,0
	–1,0	–0,5		0,0	0,5	1,0
Рис. 4.4. Полиномы Pm для функции f (x)= x					на чебышёвских сетках
На рис. 4.5 представлена погрешность аппроксимации этой же функции
полиномами Pm на чебышёвской сетке в зависимости от числа сегментов сеточ-
ной области.

99

||f –P m ||
0,2
0,15
0,1
0,05
0
2	4	8	16	32	64
Рис. 4.5. Погрешность аппроксимации функции				f (x)= x
	полиномами Pm на чебышёвских сетках

4.2. Интерполяция сплайнами

Сплайн – способ аппроксимации функции, заданной таблично, с помощью набора кусочно-полиномиальных зависимостей. Исторически понятие сплайна1 связывается с гибкой линейкой, применяемой в чертежных работах. Из курса механики деформируемых стержней известно приближенное дифференциальное уравнение изгиба упругого стержня:

EIuxxxxiv = q(x),

где Е – модуль упругости, I – момент инерции поперечного сечения, u – функция прогиба, q(x) – распределенная нагрузка. В случае отсутствия нагрузки получается однородное уравнение

uxxxxiv = 0,

решение которого представляется кубическим полиномом u(x)= C0 + C1x + C2 x2 + C3 x3 ,

где C0 , C1, C2 , C3 – постоянные интегрирования, определяемые из граничных

условий. Иными словами, гибкая линейка, помещенная на плоскости на ребро, плавно (то есть без изломов) изогнется так, что ее форму между любыми двумя соседними точками можно описать кубической параболой. Поэтому традици-

1 Spline (англ.) – гибкая линейка.

100