2190

Применив теорему равновесия к задаче определения производственного плана, можно видеть, что положительную двойственную оценку будут иметь лишь те виды ресурсов, которые полностью используются при оптимальном плане производства изделий (т.е. соответствующее ограничение выполняется как строгое равенство). Поэтому двойственные оценки определяют дефицитность используемых ресурсов. Если i-я двойственная оценка равна нулю, то по i-му виду сырья имеется резерв.

Значения двойственных оценок можно определить по симплексной таблице решения прямой задачи следующим образом: -( j cj), где j-номера столбцов единичных векторов

из исходной симплекс-таблицы (на начальной итерации); j-

окончательные оценки из последней симплекс-таблицы, соответствующие этим векторам. При этом индексы двойственных оценок определяются номером ограничения, которому они соответствуют. Например, из симплексной таблицы 6 можно определить, что двойственная оценка для трудовых ресурсов

y1* 1

, для сырья y*2 4

и для финансов y*3 0.

Необходимо заметить, что если в качестве канонической формы рассматривается задача максимизации, то суммаj cj берется без знака “-“.

Задачи дробно-линейного программирования

Общая задача дробно-линейного программирования состоит в определении максимального (минимального) значения функции

	n
	cj x j		F1
F	j 1
	n		F2
	d j xj
	j 1

при условиях

80

n

bi

a ij x j

(i 1, m);

j 1

x j

0 (j

),

1, n

где cj,

dj, bi

и

aij

–

постоянные числа,

n

n

в области

неотрица-

d j x j

0 , ( j 1, n ) и d j x j

0

j 1

j 1

тельных решений

системы линейных уравнений,

задающих

n

ограничения. Предположение, что

djx j 0 не нарушает

j 1

общности задачи, поскольку в том случае, когда эта величина отрицательна, минус можно отнести к числителю.

Сформулированная задача может быть сведена к задаче линейного программирования. Для этого следует обозначить

n	1
y0 dj	xj	и ввести новые переменные
j 1
	yi y0xj		( j		).
				1,n

Используя введенные обозначения, исходную задачу сведем к следующей - найти максимум (минимум) функции

	n
F * c j y j
при условиях	j 1
n
aij y j	bi y0 0, i
		1, m;
j 1
n
d j x j	1;
j 1

y j 0, ( j 1, n) и y0 0.

Построенная задача является задачей линейного программирования, следовательно, ее решение можно найти известными методами. Зная оптимальный план этой задачи, на

81

основе соотношений y j y 0 x j , получаем оптимальный план

исходной задачи.

Пример 6. Для производства двух видов изделий A и В используются два типа технологического оборудования. Первое изделие проходит обработку только на втором типе оборудования, второе - на первом и на втором. Время обработки каждого из изделий на оборудовании данного типа приведено в табл. 9. Там же указаны затраты, связанные с производством одного изделия каждого вида.

Таблица 9

Тип оборудования	Затраты времени (ч)
	на обработку одного изделия
	A	B
I		2
II	1	2
Затраты на производство	5	4
одного изделия

Оборудование II типа предприятие может использовать не более 52 часов. При этом оборудование I типа целесообразно использовать не менее 16 часов. Требуется определить, сколько изделий каждого вида следует изготовить, чтобы себестоимость одного изделия была минимальной.

Составим математическую модель задачи. За x1 обозначим количество выпускаемых изделий вида A, за x2 – количество изделий вида B. Себестоимость определяется следующим образом: С=З/K, где К – количество выпускаемых изделий, З - общие затраты на их производство. Тогда получим следующую задачу дробно-линейного программирования:

F	5x 1	4 x 2		min	;
	x 1	x 2
2x		2	16;
			2x 2	52;
x1
x1, x 2			0.

82

Преобразуем ограничения-неравенства данной задачи в равенства:

F	5x1	4x 2			min ;
	x1	x 2
2x 2 x 3			16 ;
			x 4 52 ;
x1 2x 2
x 1 , x 2 , , x 4 0.
Сведем данную задачу к задаче линейного программи-
рования. Для этого обозначим x			x	2		1через y0 и введем
		1

новые переменные yj y0xj ( j 1,5).

В результате приходим к следующей задаче: найти ми-

нимум функции F 5y1	4y2 при условиях
2y 2 y 3 16 y 0 0;
	2y 2 y 4 52 y 0 0;
y1
	y 2 1;
y1

y 0 , y1 , , y 4 0.

Система ограничений задачи содержит всего одну базисную переменную y4. Поэтому составим расширенную задачу путем введения двух искусственных переменных y5 и у6:

F 5 y 1	4 y 2	My 5 My 6 min при условиях
	2 y 2 y 3 16 y 0 y 5		0;
		2 y 2 y 4 52 y 0	0;
	y1
		y 2 y 6 1;
	y1

y 0 , y1 , , y 6 0.

Решение задачи методом искусственного базиса приведено в табл. 10.

83

										Таблица 10
x	c		b	5	4	0	0	0
				y1	y2	y3	y4	y0
									6	5
Y5	М		0	0	2	-1	0	-16
y4	0		0	1	2	0	1	-52
y6	М		1	1	1	0	0	0
	0			-5	-4	0	0	0
	1			1	3	-1	0	-16
y2	4		0	0	1	-1/2	0	-8
y4	0		0	1	0	1	1	-36
y6	M		1	1	0	1/2	0	-6
	0			-1	0	-2	0	-32
	M			1	0	1/2	0	-6
y2	4		0	0	1	-1/2	0	-8
y1	5		0	1	0	1	1	-36
y6	M		1	0	0	-1/2	-1	30
	0			0	0	-16/3	5	-220
	M			0	0	-1/2	-1	30
y2	4		8/30	0	1	-19/30	-8/30	0
y1	5		36/30	1	0	12/30	-6/30	0
y0	0		1/30	0	0	-1/60	-1/30	1
	220/30			0	0	-12/30	-72/30	0

Из таблицы видно, что оптимальным планом задачи яв-

ляется y1* 36 / 30; y2* 16	/ 30; y3* y4* 0; y0* 1/ 30 .
Учитывая, что yj	y0x j, находим оптимальный план

исходной задачи: x* 36; x* 16; x* 0; x* 0 . F(X*)=220/30.
1	2	3	4

84

ЛЕКЦИЯ 8 РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО

ПРОГРАММИРОВАНИЯ СРЕДСТВАМИ EXCEL

Основные этапы решения задачи линейного программирования средствами EXCEL

Решение задач в среде EXCEL начинается с ввода условий задачи. Ввод условий задачи состоит из следующих основных шагов:

-создание формы для ввода условий задачи;

-ввод исходных данных;

-ввод зависимостей из математической модели;

-назначение целевой функции;

-ввод ограничений и граничных условий.

Пример Требуется определить, в каком количестве необходимо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4 для изготовления которой требуются ресурсы трех видов: трудовые ресурсы, сырье, финансы. Нормы расхода ресурсов каждого вида для выпуска единицы продукции, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл. 11. Количество расходуемых ресурсов не должно превышать имеющихся запасов [4].

Данная задача относится к задаче планирования при ограничениях на ресурсы, распределительного типа.

					Таблица 11
Ресурсы		Виды продукции				Запасы
	Прод.1	Прод.2	Прод.3	Прод.4		ресурсов
Трудовые	3	1	2	4		440
Сырье	1	8	6	2		200
Финансы	1	4	7	2		320
Прибыль	7	3	6	12

85

Математическая модель для решения данной задачи будет иметь следующий вид:

F=7x1+3x2+6x3+12x4 max; 3x1+x2+2x3+4x4 440; x1+8x2+6x3+2x4 200;

x1+4x2+7x3+2x4 320;

xj 0, j=1,4.

Рассмотрим последовательность работ при решении этой задачи средствами Exсel. Форма для ввода условий данной задачи может иметь следующий вид:

Рис. 16

Весь текст на рис. 16 (и в дальнейшем) является комментарием и на решение задачи не влияет. Далее необходимо ввести в сформированную форму исходные данные (коэффициенты в целевой функции и ограничениях, а также направление оптимизации целевой функции и знаки ограничений (рис. 17)

Рис. 17

86

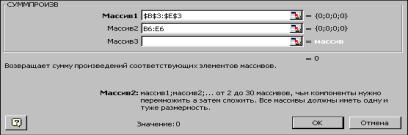
При этом ячейки B3:E3 являются изменяемыми и в них будут заноситься значения переменных.

Ввод функциональных зависимостей для целевой функции и ограничений осуществляется с использованием Мастера функций. Для этого необходимо активизировать требуемую ячейку (F6) и вызвать Мастер функций. В левой части появившегося диалогового окна нужно выбрать категорию функции Математическая, а в правом окне выделить функцию СУММПРОИЗВ и нажать клавишу ОК. Затем на экране отобразится диалоговое окно второго шага (рис. 18), где требуется ввести как первый (B$3:E$3), так и второй массивы (B6:E6). При вводе первого массива используются абсолютные ссылки на ячейки, при вводе второго - относительные, что в дальнейшем будет удобно при копировании формул. Во все окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, адреса которых необходимо ввести.

Рис. 18

Зависимости для левых частей ограничений вводятся аналогично. При этом необходимо лишь менять адреса ячеек. Для ускорения и удобства ввода можно скопировать содержимое ячейки F6 в ячейки F9, F10 и F11 (при этом все относительные ссылки изменятся автоматически).

87

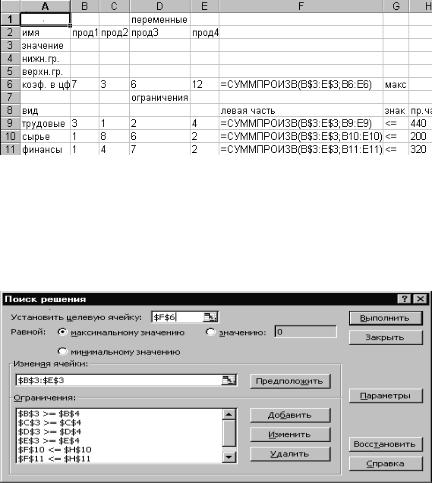
Окончательная таблица с исходными данными представлена на рис. 19 (для наглядности выбран режим представления формул, который использовать не обязательно).

Рис. 19

После окончания ввода исходных данных осуществляется вызов программы Поиск решения. Для этого необходимо выбрать в меню пункт Сервис, а в нем – Поиск решения, в результате чего на экране появится окно поиска решения (рис. 20).

Рис. 20

В окне Установить целевую ячейку требуется ввести имя ячейки, в которую введена зависимость для целевой функции (в данном случае F6). В качестве направления опти-

88

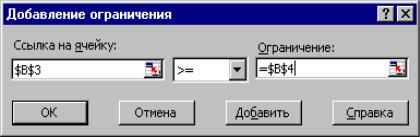
мизации выбирается максимизация. В окне Изменяя ячейки вводятся адреса ячеек, соответствующих варьируемым переменным задачи (B3:E3). Далее необходимо ввести ограничения. Для добавления ограничений выбирается пункт Добавить, после чего появляется окно добавления ограничений

(рис. 21)

Рис. 21

Вводятся граничные условия для переменных

(Прод1 - Прод4) 0: B3>= B4, C3 >= C4, D3 >= D4, E3 >= E4 (нулевые значения ячеек B4-E4 можно не устанавливать). Ограничения можно также ввести в виде B3 >= 0, C3 >= 0, D3

>= 0,	E3 >= 0. Затем вводятся ограничения на ресурсы:
F9 <=	H9, F10 <= H10, F11 <= H11. Ограничения вводят по-

следовательно. Сначала выбирается пункт Добавить, далее в появившихся диалоговых окнах вводится левая часть, знак и правая часть каждого ограничения. После ввода последнего ограничения и нажатия OK произойдет возврат в окно Поиск

решения.

Заполненная в результате ввода ограничений форма поиска решений представлена на рис. 20. Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения. Перед началом решения необходимо установить параметры решения, для чего в окне поиска решения выбрать команду параметры. Диалоговое окно параметров поиска решения представлено на рис. 22.

89