2790

мента импульса тела получим

или, в координатной форме (индекс опускаем),

Последняя сумма, представляет собой тензор инерции (12.8), таким образом

С учетом (12.15), вращательную кинетическую энергию можно записать в виде

или

где I – матрица	, рассматриваемая как линейный оператор,
преобразующий вектор в вектор L по формуле (12.15).

Представим угловую скорость в виде	, где –
единичный вектор, направленный вдоль . Тогда

161

где скалярная величина

называется моментом инерции отно-

сительно оси вращения		, проходя-
щей через центр инерции.
	Момент инерции	относительно
оси	можно определить также как

сумму произведений масс материаль-

ных точек		на квадраты расстоя-
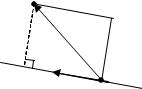
ний	от этих точек до данной оси
(см. рис. 12.1):

O’(C)

Рис. 12.1

12.2. Тензоры второго ранга. Главные оси тензора

Пусть некоторое свойство связывает два вектора и следующим линейным преобразованием:

или, в развернутом виде,

Девять коэффициентов

можно записать в виде таблицы

162

которую называют тензором второго ранга.

Подобно матрице направляющих косинусов (11.2), которую можно рассматривать как линейный оператор, преобразующий компоненты вектора при преобразовании осей координат [см. формулы (11.4-6)], тензор может рассматриваться как оператор G, который, действуя на вектор , преобразует его в другой вектор (при неизменных осях координат). Соотношение (12.21) можно записать в операторной форме:

Действие оператора G на вектор записывается в виде произведения и заключается в умножении матрицы этого оператора (12.23) на матрицу-столбец, составленную из координат вектора .

Ранг тензора равен числу индексов в обозначении компонентов тензора , а число компонентов тензора равно (число 3 соответствует размерности пространства, в котором заданы векторы и , r – ранг тензора).

Скалярные величины называют тензорами нулевого ранга ( , а векторы – тензорами первого ранга (31 = 3). Существуют также тензоры третьего, четвертого и т.д. рангов.

Для определения понятия тензора можно использовать закон преобразования его компонентов при преобразовании системы координат. Так, три величины , , образуют полярный вектор (полярный тензор первого ранга), если при преобразовании системы координат они изменяются по закону (11.7). Легко показать, что компоненты тензора второго ранга (полярного) преобразуются по закону

Тензор второго ранга называется симметричным, если и антисимметричным, если (для любых

).

Покажем, что симметричный тензор второго ранга можно

163

геометрически интерпретировать как поверхность второго порядка. Рассмотрим уравнение

где	– некоторые коэффициенты. Положив	и вы-
полнив суммирование по и по , получим

Мы получили уравнение поверхности второго порядка, центр которой расположен в начале координат. Данная поверхность может быть эллипсоидом или гиперболоидом.

Согласно соотношению (11.9), при переходе от старых осей координат к новым осям уравнение (12.26) преобразуется в уравнение

где

Сравнивая соотношения (12.29) и (12.25), заключаем, что коэффициенты поверхности второго порядка преобразуются также, как компоненты тензора второго ранга. Поэтому по-

верхность (12.27) называется характеристической поверхно-

стью для симметричного тензора второго ранга 1.

Известно, что оси координат можно выбрать таким обра-

1 При преобразованиях системы координат изменяются значения коэффициентов в уравнении характеристической поверхности, однако сама характеристическая поверхность при этом не меняется.

Отметим также, что в уравнении характеристической поверхности величины , , имеют размерность .

164

зом, что уравнение поверхности второго порядка примет упрощенный вид

Соответствующие оси координат называют главными осями поверхности второго порядка и соответствующего тензора. Все главные оси характеристической поверхности являются взаимно ортогональными. Из (12.30) видно, что длины

полуосей характеристической							поверхности будут равны
.
	Если все коэффициенты						, ,	положительны, то ха-

рактеристической поверхностью будет эллипсоид. Если два коэффициента положительны, а один отрицателен, поверхность будет однополостным гиперболоидом. Если один коэффициент положителен, а два других отрицательны, то поверхность будет двуполостным гиперболоидом. Наконец, если все три коэффициента отрицательны, поверхность будет мнимым эллипсоидом.

В результате преобразования к главным осям тензор преобразуется к диагональному виду:

Величины	,	,	называют главными значениями
ра .
Пусть векторы		и	связаны преобразованием

Если тензор привести к главным осям, то это уравнение примет вид

В случае, когда вектор параллелен одному из главных

165

направлений тензора	, например, оси	, векторы и бу-
дут параллельны:	. Это утверждение останется вер-

ным при любом выборе осей координат, т.к. векторы p и q (рассматриваемые как направленные отрезки) от этого выбора, очевидно, не зависят.

Таким образом, можно дать следующее определение главной оси тензора: если при преобразовании (12.32) вектор коллинеарен вектору , то направление вектора является направлением главной оси тензора .

Рассмотрим вопрос об определении главных осей и главных значений симметричного тензора . Если направление вектора совпадает с направлением главной оси тензора , то, как следует из приведенного выше определения главной оси, должно выполняться равенство

где – постоянный коэффициент. Выражение (12.34) соответствует системе трех ( = 1, 2, 3) линейных однородных уравнений относительно переменных , . Данная система имеет нетривиальное решение, если ее определитель равен нулю:

Корни этого кубического уравнения , ,	представляют
собой главные значения тензора .

После подстановки какого-либо из главных значений, например, , в систему уравнений (12.34), можно определить отношения , т.е. направление главной оси тензора, соответствующее собственному значению .

12.3. Тензор инерции

Обратимся теперь к тензору моментов инерции , кото-

166

рый, в соответствии с формулой (12.15), преобразует вектор угловой скорости твердого тела в вектор момента импульса

. Согласно определению (12.8), этот тензор имеет вид:

					(12.36)
Диагональные компо-
ненты	тензора инерции			,
,	называют осевыми
моментами инерции, а все
остальные		компоненты		–
центробежными			момента-
ми инерции.
Тензор			является
симметричным			тензором
второго ранга:			= .	Так
как все диагональные эле-
менты тензора инерции по-
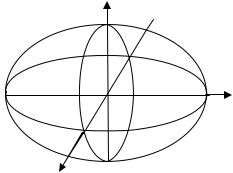
ложительны,		его характери-				Рис. 12.2

стической поверхностью будет эллипсоид – эллипсоид инерции (рис. 12.2). Надлежащим

выбором осей		подвижной системы координат	,	,
(см. рис.	12.2)	тензор инерции можно привести к диагонально-
му виду:

Величины , , называют главными моментами инерции.

После приведения тензора инерции к главным осям формулы для кинетической энергии и момента импульса твердого тела (12.9) и (12.15) примут вид:

167

Тело, у которого все три главных момента инерции различны, называют асимметричным волчком. Если два главных момента инерции равны друг другу, а третий отличен от первых двух, то тело называют симметричным волчком. Наконец, если все три главных момента инерции равны, то тело назы-

вают шаровым волчком.
Для шарового волчка	, т.е. векторы	и	совпа-
дают по направлению. В общем случае векторы		и	не па-

раллельны. Как видно из формул (12.39), для произвольного тела направления векторов и совпадают только при вращении тела вокруг одной из его главных осей инерции.

У шарового волчка эллипсоид инерции вырождается в сферу, соответственно в качестве главных осей инерции могут быть выбраны любые три ортогональные оси, проходящие через центр инерции. Шаровым волчком является однородный шар, однородный куб и любое другое тело, у которого

== .

Вслучае симметричного волчка, у эллипсоида инерции равны две полуоси. Такой эллипсоид называют эллипсоидом вращения (его можно получить, вращая эллипс вокруг одной

из главных осей). Пусть =	≠ , тогда ось вращения эллип-
соида совпадает с главной	осью инерции , а две других

главных оси инерции должны лежать в перпендикулярной к оси вращения плоскости , в остальном выбор их направления произволен.

В п. 10.2 было показано, что определение главных направлений и главных значений симметричного тензора второго ранга требует решения кубического уравнения вида (12.35). Поиск главных осей тензора инерции значительно упрощается, если тело обладает определенной симметрией: той же симмет-

168

рией, очевидно, должно обладать расположение центра инерции и главных осей инерции.

Например, если тело обладает осью симметрии, то его центр инерции лежит на этой оси, кроме того, данная ось совпадает с одной из главных осей инерции. Две других оси инерции будут перпендикулярны к оси симметрии. Отметим также, что если порядок оси симметрии выше второго, то тело будет симметричным волчком. В самом деле, в этом случае оси инерции, перпендикулярные оси симметрии, могут быть повернуты на угол, отличный от 180o, а такой произвол в выборе осей симметрии возможен лишь для симметричного волчка.

Если тело обладает плоскостью симметрии, то центр инерции и две оси инерции будут лежать в этой плоскости, а третья ось инерции будет перпендикулярной к ней.

Ранее, рассматривая тен-
зор момента инерции, мы по-
мещали начало системы коор-
динат	, т.е. точку , в центр
инерции	. В некоторых слу-
чаях удобно вычислять момент
инерции	в системе координат
(так же жестко связанной с
телом), начало которой лежит в
точке O'', смещенной относи-
тельно центра инерции на не-
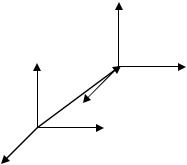
который вектор (рис. 12.3). В		Рис. 12.3
этой системе координат мо-
мент инерции равен

Учитывая, что	(где – -я координата точки
O'' в системе координат ) и	(т.к. – центр инер-

ции), легко получить следующее соотношение, связывающее

169

между собой тензоры и :

Выражение (12.41) в тензорном виде выражает теорему Штейнера, согласно которой момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями. Чтобы это показать, найдем из выражения (12.41) осевой момент :

где – расстояние между осями и .

12.4. Свободное вращение симметричного волчка

Рассмотрим вращение тела, на которое не действуют внешние силы. В этом случае в инерциальной системе отсчета центр инерции движется с постоянной скоростью или покоится. Поэтому, мы можем исключить из рассмотрения поступательное движение тела, выбрав внешнюю инерциальную сис-

тему отсчета	так,	чтобы относительно нее центр инерции
покоился.
Так как система замкнута, выполняется закон сохранения
момента импульса:		. Данного закона достаточно для

описания движения свободных шарового и симметричного волчков.

Если тело является шаровым волчком, то Таким образом, свободное вращение шарового волчка

представляет собой равномерное вращение вокруг постоянной оси.

Обратимся теперь к свободному вращению симметрично-

170