3267

		10		2				15				3			,
	P(H1 )						, P(H2 )
		25		5				25				5
				9								10			;
	P(A / H1 )						; P(A / H2 )
				24								24
	и следовательно, по формуле полной вероятности
																10		9		15		10
	P(A / H2 ) P(H1 )P(A / H1 ) P(H2 )P(A / H2 )
																25		24		25		24
	0, 4.
	2) Найдем вероятность P(A / H1 )							10				0, 4 .				Таким				образом,
								25

шансы получить знакомый билет – одинаковы.

Пример. По каналу связи передается одно из двух сообщений: сообщение х1 и х2. Пусть получено х1. Какова вероятность того, что передавалось х1? Из статистического изучения линии связи известно, что сообщение х2 передается в среднем в два раза чаще чем х1. Известно также, что сигнал х1 искажается в 10% случаев, а х2 - в 20% случаев.

Выбираем гипотезы:

Н1 - посылалось сообщение х1; Н2 - посылалось сообщение х2.

Находим вероятность гипотез: P(H1 ) 13 , P(H2 ) 23 .

Пусть событие А - получено сообщение х1. Так как по условию

х1 искажается в 10% случаев, то P(A / H1 )	0, 9 ; а х2 - в 20%
случаев, то P(A / H2 ) 0, 2 . Первая	вероятность есть

вероятность того, что получено х1, при условии, что передавалось х1; вторая вероятность того, что получено х1, при условии, что передавалось х2. Надо найти вероятность того, что передавалось х1, если получено х1, т.е. P(H1 / A) . По формуле

Байеса получим

	P(H1	/ A)	P(H1 )P(A / H1 )
			P(H1 )P(A / H1 ) P(H2 )P(A / H2 )

41

	1			9
							9					1
	3			10									,	т.е. канал связи удовлетворительный.
1		9				2		2 13				2
9	10			3			10

Пример. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей группы - 5 студентов. Вероятность того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7; 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Найти вероятность того, что студент принадлежал к первой группе.

Решение. Выбираем гипотезы Hi (i 1, 2, 3) - студент

принадлежит к i - вой группе. Событие А - студент попал в сборную института. Из условия следует

P(H )	4		, P(H			)		6	, P(H		)	5			, P(A / H )						0,9;
					2					3
1	15						15					15							1
P(A / H2 ) 0, 7; P(A / H3 ) 0,8 .
По формуле Байеса
																	4		9
				P(H1 )P(A / H1 )																						18
P(H1 / A)																	15 10											.
				3								4				9		6		7		5			8		59
				P(Hi			)P(A / Hi )
												15			10		15		10		15			10
				i 1

4.2. Последовательность независимых испытаний. Схема

Бернулли

Рассмотрим эксперимент, в котором проводятся последовательные независимые испытания и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.

Последовательные испытания называются независимыми, если вероятность осуществления любого

42

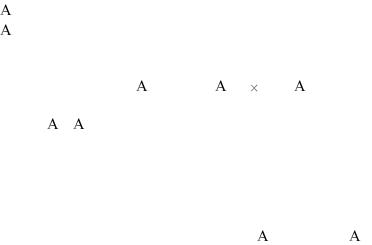
исхода в k-м по счету испытании не зависит от реализации исходов предыдущих испытаний.

Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами («успех» и «неуспех») и с неизменными вероятностями "успеха" р и "неуспеха" 1-p=q в каждом испытании. Такая схема называется схемой Бернулли. Построим вероятностное пространство в схеме Бернулли. Обозначим событие, которое мы назвали "успех" буквой Y, а событие "неуспех" – буквой Н. Тогда, если эксперимент состоит из одного испытания, вероятностное пространство (Ω,

,Р) определяется следующим образом: Ω={Y,H}, ={Ø,Y,Н,Ω}, Р(Y)=р, P(H)=1-p=q. Если эксперимент состоит из двух испытаний, то соответствующее вероятностное

пространство

(Ω2, 2, Р2)=(Ω, , Р) ( Ω, , Р), Ω2=Ω·Ω={(Y,Y), (Y,H), (H,Y), (H,H)};

2= · – есть множество всех подмножеств пространства элементарных событий Ω2 и содержит 24 элементов. Вероятности Р2(Ω) вычисляют с учетом независимости исходов по формулам

Р2(YY)=р2; P2(HY)=Р2(YH)=pq; Р2(НН)=q2. И так далее.

Если эксперимент состоит из п последовательных независимых

испытаний в схеме Бернулли, то (Ωп,			п, Рп)=[x(Ω, , Р)]n
		ω1	ω2
		n	n
Fп=[хF]п – множество всех подмножеств Ωn.
Вероятности
k	n-k	k	n-k
		43

Простейшей задачей в схеме Бернулли является задача нахождения вероятности того, что в серии из п испытаний "успех" наступит ровно k раз. Поскольку при этом не имеет значения, когда именно в этих испытаниях будут наблюдаться k успехов, то событие Аk, состоящее в наступлении k успехов, является объединением всех различных элементарных событий

ω	п	в которых Y встречается k раз.
	Всего таких элементарных событий в Аk		Сnk , а

поскольку они несовместимы, то искомая вероятность дается равенством

Аk YY...YHH...HHYHYH...YH ...

k	n-k	Y-k раз, Н	n-k раз
Рп Аk Рп k	Cnk pk qn k ,	k 0, 1,..., n .	(3)

Эта формула называется формулой Бернулли.

Пример. Передается шифрованное сообщение – импульсно-кодовая комбинация, состоящая из 6 импульсов и 4 вакансий. Действует помеха. В результате любой из импульсов может быть подавлен с вероятностью 0,04 и на любой вакансии появиться ложный импульс с вероятностью 0,1. Определить вероятность того, что а) в кодовой комбинации окажутся подавленными ровно два импульса, б) в кодовой комбинации появится два ложных импульса.

Решение. а) События подавления импульса и появления ложного импульса независимы. Пользуемся формулой Бернулли:

P6 (2) C62 (0,04)2 (0,96)4 0,0204

б) P4 (2) C42 (0,1)2 (0,9)2 0,0486 .

4.3. Локальная теорема Муавра-Лапласа.

Если в схеме Бернулли наряду с числом испытаний n велики произведения np и nq, то следует применять формулы Муавра-Лапласа локальную или интегральную.

Локальная теорема Муавра-Лапласа.

44

Если в схеме Бернулли число испытаний n велико, то для всех m справедлива приближенная формула (локальная формула Муавра-Лапласа)

1

m

np

1

x2

P (m)

(x) , где x

, а

(x)

e 2 .

n

npq

npq

2

Значения функции (x) содержатся в таблицах.

Пример. Вероятность поражения мишени стрелком при одном выстреле p=0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. По условию n=10, k=8, p=0,75, q=0,25.

Воспользуемся формулой Муавра-Лапласа:

					P (8)						1				(x)	0, 7301 (x) .
					10			10			0, 75 0, 25
				Вычислим определяемое данными задачи значение
x	m np				8			10 0, 75					0,36 . По таблице				(0,36)	0,3739 .
		npq			10			0, 75 0, 25
Тогда P (8)					0, 7301 0, 3739								0, 273 .
	10
		4.4. Интегральная теорема Муавра-Лапласа.
		Если в схеме Бернулли число испытаний n велико, то
для вероятности P(k1											k		k2 ) , того,			что	число	успехов
заключено в пределах от k1													до k2 , справедливо приближенное

соотношение (интегральная формула Муавра-Лапласа):

P(k1

k

k2 )

Ф(x2 ) Ф(x1 ) , где

k1

np

k2

np

1

x

y2

x

; x

,Ф(x)

e 2 dy .

1

npq

2

npq

2

Значения функции Ф(x) содержатся в таблицах.

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди

45

400 случайно отобранных деталей окажется непроверенных от

70 до 100 деталей.

Решение. По условию, p=0,2; q=0,8; n=400, k1=70, k2=100. Воспользуемся формулой Муавра-Лапласа:

P400 (70					k					100)					Ф(x '')		Ф(x ') .
Вычислим x '	и x '' :
x '		k1			np					70					400 0, 2						1, 25
				npq						400						0, 2	0,8
x ''			k2		np					100						400	0, 2			2, 5
					npq					400						0, 2	0,8
По					таблице												Ф(x ')				Ф( 1, 25) 0,3944 ,
Ф(x '') Ф(2,5) 0, 4938 .
Искомая вероятность
P400 (70	k			100)							Ф(2, 5) Ф( 1, 25)										0,8882 .

4.5.Наивероятнейшее число успехов

впоследовательности независимых испытаний

Исследуем, как меняется вероятность Pn(k) как функция k при постоянном п. Для этого рассмотрим отношение

Pn k 1 Cnk 1 pk 1qn k 1

n! n k !k !

p n k p

.

P k

Ck pk qn k

n k 1 ! k 1 !n!

q

k 1

q

n

n

Отсюда

следует

рекуррентная

формула

для

биномиальных вероятностей

P

k 1

n

k

p

P k .

(4)

n

k

1

q n

Из этой формулы получается, что Рп(k+1)>Pn(k),

если

n

k

p

1, или (n-k)p>(k+1)q , np-kp>kq+q ,

np- q >k,

k

1

q

так как (р+q)=1. То есть вероятность Рп(k) возрастает при переходе от k к k+1 и, еcли np- q >k, и, наоборот, убывает при

46

переходе от k к k+1, если np-q<k. Если же np-q=k , то

Рn(k)=Рп(k+1).

Итак, из анализа рекуррентной формулы (4) видно, что вероятность Рп(k) с увеличением k сначала возрастает, затем достигает максимума и при дальнейшем росте k убывает.

Наиболее вероятное число M успехов в серии п независимых испытаний удовлетворяет неравенству

пр- q ≤М<np- q +1=пр+р.

Вывод. Если число р(п+1) целое, то наивероятнейшее число успехов имеет два значения: значение M1=p(n+1) и значение M2=np-q . Если р(п+1) – дробь, то наивероятнейшее число успехов равно первому целому числу, меньшему числа p(n+1).

Заметим, что при достаточно малой вероятности успеха р, такой, что np-q ≤0, вероятность Рп(k) не возрастает ни при каких k≥0. В этом случае вероятнее всего, что при п испытаниях не будет ни одного успеха.

Пример. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, р=0,9. Найти наивероятнейшее число элементов, выдержавших испытание.

Решение. В этой задаче можно считать испытания независимыми и применить схему Бернулли. п=15; р=0,9;

q =0,1. Найдем М.

М=[np- q ]=[15·0,9-0,1]=[13,4]=14.

Пример. Сколько нужно произвести независимых испытаний с вероятностью появления события в каждом испытании р=0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?

Решение. Снова будем рассматривать схему Бернулли.

р=0,4; q =0,6; М=25.

М=[np-q]=25; [n·0,4-0,6]=25 n=64.

Пример. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день

47

с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число поступивших заявок в день и вероятность получения этого числа заявок.

Решение. В данном случае n=10; p=0,4; p(n+1)=4,4.

Наивероятнейшее число М заявок равно целой части числа p(n+1), т.е. М=4. Вероятность поступления четырех заявок из десяти вычисляем по формуле Бернулли

P (4)	C4	(0, 4)4 (0,6)6	0, 251.
10	10

5. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ. ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

5.1. Предварительные замечания

Одним из основных понятий теории вероятностей является понятие случайной величины (СВ). Прежде чем переходить к формальному ее определению, остановимся на позициях качественного описания. Рассмотрим примеры.

1.Число вызовов, поступающих от абонентов на телефонную станцию в течение определенного промежутка времени, дает нам пример случайной величины, принимающей те или иные значения в зависимости от случайных обстоятельств.

2.Скорость молекул гaзa в сосуде не остается неизменной, а меняется в зависимости от столкновений с другими молекулами. Этих столкновений чрезвычайно много даже в течение короткого промежутка времени. Таким образом, изменение скорости молекул газа носит случайный характер.

48

Приведенные примеры показывают, что со случайными величинами приходится иметь дело в самых различных областях науки, техники, обслуживания, поэтому, естественно, возникает потребность в создании методов изучения и описания случайной величины.

Для этого в каждом конкретном случае нужно выделить общие для них моменты. Так, в рассмотренных примерах и число вызовов, и скорость молекул под влиянием случайных обстоятельств принимают различные значения. Заранее указать, какое значение примет соответствующая величина, нельзя, так как оно меняется случайным образом от испытания к испытанию.

Таким образом, для того чтобы знать случайную величину, прежде всего необходимо знать те значения, которые она может принимать. Однако одного перечня значений СВ еще недостаточно, чтобы по нему можно было делать какие-либо существенные выводы. Действительно, если в примере со скоростью молекул рассмотреть газ при разных температурах, то возможные значения скорости молекул останутся теми же самыми, тогда как состояния газа будут различными. Отсюда можно заключить, что для задания случайной величины необходимо знать не только то, какие значения она может принимать, но и как часто, то есть с какой вероятностью она принимает эти значения.

Разнообразие СВ весьма велико. Число принимаемых значений может быть конечным, счетным и несчетным. Значения могут быть расположены дискретно или заполнять интервал сплошь. Для того, чтобы задавать вероятности значений СВ, столь различных по своей природе, и притом задавать их одним и тем же способом, в теории вероятностей вводят понятие функции распределения случайной величины

(ФР).

Пусть X - случайная величина и х - произвольное действительное число. Вероятность того, что X примет

49

значение, меньшее х, называется функцией распределения вероятностей СВ X.

F(х)=Р(Х<х).

Резюмируя сказанное, оставаясь на позициях качественного описания, можно так определить СВ.

Случайной величиной называется переменная величина, значения которой зависят от случая и для которой определена функция распределения вероятностей.

Перейдем теперь к строго формальному определению понятия СВ.

5.2.Определение случайной величины

ифункции распределения вероятностей

Пусть задано Ω - пространство элементарных событий. Под событием мы понимаем любое подмножество из Ω: А Q. К событиям, определенным таким образом, неудобно непосредственно применять аппарат математического анализа. Для того, чтобы это было возможно, вводят случайные величины.

Числовая функция, определенная на пространстве элементарных событий, называется случайной величиной X. Требуется, чтобы при любом х существовала определенная вероятность того, что случайная величина Х меньше х.

Рассмотрим подробнее это определение. Итак, задано пространство элементарных событий Ω={ωi}. Каждому элементарному событию ставится в соответствие число хi. В результате испытания появляется одно из элементарных событий, например, ωi, при этом СВ X принимает значение xi, соответствующее этому элементарному событию. Таким образом, X=f(ω), то есть случайная величина есть числовая функция, аргументом которой служит событие. Рассматриваются только такие СВ, для которых определена вероятность того, что CB меньше х. Таким образом, приходим к понятию функции распределения вероятностей.

50