585

Основные свойства числовых проекций вектора в прямоугольной системе координат:

1)проекции вектора не изменяются при параллельном переносе вектора или оси, на которую вектор переносится;

2)проекция суммарного вектора равна алгебраической сумме

r r

одноименных проекций слагаемых векторов: если c = a + b = = cxi + cy j + czk то cx = ax + bx , cy = ay + by , cz = az + bz ;

3) каждая проекция вектора равна разности соответствующих координат конечной и начальной точек вектора

AB = (xB − xA, yB − yA, zB − zA );

Замечание. Если необходимо определить расстояние между двумя точками, то принимая их за начальную и конечную точки вектора, длину вектора можно вычислить как расстояние между точками:

uuur 2

AB = 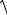(xB − xA )2 + (yB − yA ) + (zB − zA )2 .

4) при умножении вектора на действительное число все его проекции на координатные оси умножаются на то же число

	r	= (λax ,λay	,λaz ).
	λa
v	r
Если a	|| b , то b = λa и получаем

аналитическое условие коллинеарности векторов

ax = ay = az . bx by bz

Теорема (аналитическое условие коллинеарности)

Векторы a = (a1, a2, a3 ) и b = (b1, b2,b3) коллинеарны тогда и

только когда a1 = a2 = a3 . В случае равенства нулю одного или b1 b2 b3

нескольких знаменателей, соответствующие равенства следует понимать как пропорции.

123

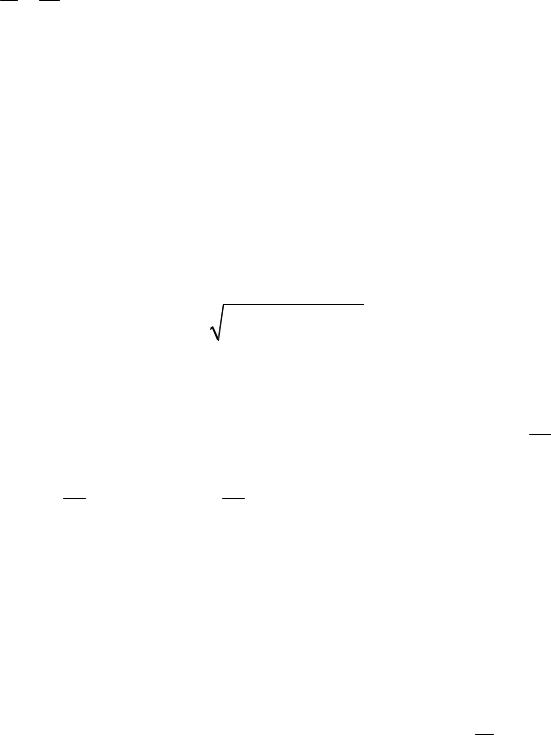
Замечание. Всюду в дальнейшем выражения, подобные равенству

a1 = a2 , будем понимать как пропорции, чтобы отдельно не оговаривать b1 b2

случай равенства знаменателей нулю.

Пример 1. При каких значениях параметров α и β векторы

r

v

= 3i

− j + 2k .

u и v коллинеарны: u

= αi + 3 j + βk , v

Решение:

u

x

=

uy

=

u

z

α

=

3

=

β

. Из

пропорции следует:

3

−1

2

vx

vy

vz

α = −9; β = −6.

Пример 2. Даны координаты вектора ax = 4; ay = −12 и его

модуль

v

=13. Найти третью координату, определить направля-

a

ющие косинусы вектора.

r

Решение: 13 =

=

42

+ (−12)2 + az2 .

a

Решив это уравнение, получим az = ±3. Таким образом, опре-

делены два вектора: a = (4; −12; 3)

r

− 3).

и a* = (4; −12;

Направляющие

косинусы

вектора

a:

cosα =

ax

=

4

,

r

a

13

cosβ =

ay

= −

12

, cos γ =

a

=

3

r

rz

.

13

a

a

13

Проверка: cos2 α + cos2 β + cos2 γ =

16

+

144

+

9

=1.

169

169

169

r*

Аналогично определяются направляющие косинусы вектора a .

3.5.60. Деление отрезка прямой в данном отношении

При решении геометрических задач методами векторной алгебры часто бывает необходимо найти координаты точки M, де-

лящей заданный отрезок AB в заданном отношении m = λ. n

Тогда координаты точки M определяются по формулам:

x =

xA + λxB

;

y

M

=

yA + λyB

;

z

M

=

zA + λzB

.

M

1

+ λ

1

+ λ

1

+ λ

124

Пример. На отрезке AB, где A(1, 2,6) и B(6, 12,21) найти

точку M такую, что

AM

=

2

.

MB 3

2

xA + λxB

1+

6

Решение: x

=

=

3

= 3;

M

1+ λ

+

2

1

3

yA + λyB

2 +

2

12

zA + λzB

6 +

2

21

y

M

=

=

3

= 6

;

z

M

=

=

3

=12.

1+ λ

1+

2

1+ λ

+

2

1

3

3

Задачи к разделу 3.50

3.5.1. На плоскости даны четыре точки

A(2; 3); B(−3;4);

C (0; − 5); D(3; 0):

а) найти координаты вектора 2AB + 5BC ;

б) найти длину и направляющие косинусы вектора OB , где

	O – начало координат;
	в) разложить вектор AD по базе AB , AC .	r
	r			(	)
	3.5.2. Известны координаты векторов c = 2a + 5b =					и
				1; 2; 3
	r		a и b .
	d = a + 3b = (4; 5; 6). Найти координаты векторов

3.5.3.Вектор a составляет с положительным направление оси OX угол 30°, а с положительным направлением оси OZ – угол 90°. Какой угол составляет вектор a с положительным направлением оси OY?

3.5.4.Вектор a составляет с положительными направлениями координатных осей в пространстве равные углы. Найти координаты этого вектора, если его длина равна 3.

(

3.5.5. В

пространстве

заданы

пять

точек A(2; 3; − 5);

B

)

(

0; 5;

)

; D

(

−5; 6; 5

)

, E

(

−3; 1; 2

)

:

−3 ;4;1 ; C

−1

r

= 3AB − 2AC + 5AD;

а) найти координаты вектора a

б) найти длину и направляющие косинусы вектора a;

в) проверить, будет ли четырехугольник ABCD трапецией;

г) проверить, будет ли четырехугольник

ABCD параллело-

граммом;

125

д) разложить вектор AD по базе AB , AC , AE .

3.5.6. Даны три точки A(2; 3); B(−3;4); C (0; − 5). Найти координаты центра и радиус окружности, проходящей через эти

точки.

(

)

(

)

(

)

3.5.7. Даны четыре точки B

0; 5; −

; D

−5; 6; 5

,

−3 ;4;1 ; C

1

E(−3; 1; 2). Найти координаты центра и радиус сферы, проходя-

щей через эти точки.

A(1, 2,3) и B(4, 5,6)

3.5.8. На отрезке

AB , где

найти точку

M такую, что

а)

AM

=

2

;

б)

AM

=

5

;

в)

AM

= 1; г)

AM

=

1

.

MB 5

MB 2

MB

MB

5

3.5.9.

Даны

координаты

середин

сторон

треугольника

A(2; 3); B(−3;4); C (0; − 5). Найти координаты его вершин. 3.5.10. Даны координаты двух смежных вершин параллело-

грамма A(2; 3) и B(−3;4) и точка пересечения его диагоналей

C (0; − 5). Найти координаты двух других вершин.

3.60. Скалярное произведение векторов

Определе ние: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними

r	b =		r				b		cosα .
a			a

Из определения скалярного произведения следует, что

r	b =		r		Πprb =		b		r
a			a						Πpra .
					a				b

Свойства скалярного произведения:

Для любых векторов a и b верно:

rr

1)a b = b a;

rr = r 2

2)a a a .

r

Если a ≠ 0 и b ≠ 0, то

r

a b > 0 тогда и только тогда, когда угол α острый;

r

a b < 0 тогда и только тогда, когда угол α тупой;

r

a b = 0 тогда и только тогда, когда угол α прямой.

126

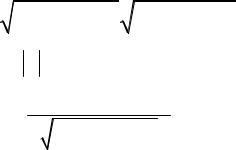
Теорема (скалярное произведение и линейные операции)

1)	Для любых векторов a и b и любого числа λ:
		r		r	b );
	(λa) b = λ(a
2)	Для любых векторов a, b , c :
	r	r	r	r	r
	(a	b) c	= a	c + b c .

Замечание. Из теоремы следует, что при раскрытии скобок в выражениях, содержащих операции векторного сложения, вычитания, умножения на число и скалярного умножения можно действовать так же, как и при раскрытии скобок, содержащих операции с числами.

Теорема (скалярное произведение в координатах)

r	+ a2b2 + a3b3 .
Если a = (a1, a2, a3 ) и b = (b1, b2,b3) , то a b = a1b1
3.6.10. Геометрические приложения
скалярного произведения векторов
r	r	π	= 0	,
1) Если векторы a и b ортогональны, т.е. cos(a, b )= cos		2

то из определения скалярного произведения следует условие ор-

										r	= 0.
тогональности векторов в векторной форме: a b
2) Если a = (a1, a2, a3 ) и b = (b1, b2,b3) , то угол между этими
векторами можно вычислить по формуле
r r			a b + a b				+ a b
cos(a, b )=			1	1	2	2		3	3				;
		a2	+ a2		+ a2		b2	+ b2		+ b2
1				2	3		1		2	3

rr

3)Учитывая, что a b = a Πparb , получим формулу

Πparbr = a1b1 + a2b2 + a3b3 ;

a12 + a22 + a32

4) Скалярное произведение вектора на орт оси позволяет определить координату (числовую проекцию) вектора на ось,

r

например, a1 = a i .

127

r

= −i

+ j и

Пример 1. Определить угол между векторами a

b = i − 2 j + 2k .

r

r

a b

+ a

b

y

+ a

b

Решение: cos(a,b )=

x x

y

z

z

=

a2

+ a2

+ a2

b2

+ b2 + b2

x

y

z

x

y

z

=

−1 1+1

(

−2

)

+ 0 2

=

−3

= −

1

.

( )

2

2

2

2

(

)

2

2

2

9

2

−1 +

+ 0

+ −2 + 2

1

1

(

r

v

)

=

3π

Значит,

a,

b

4

r

.

+ j + 2k

b = i − j + 4k .

Пример 2. Даны векторы

и

a = i

Определить проекцию вектора a на вектор b .

axbx + ayby + azbz

1 1+1 (−1)+ 2 4

r

4 2

Решение: Πpra

=

r

=

=

.

b

b

2

(

)

2

2

3

1 + −1

+ 4

При решении геометрических задач с помощью формул векторной алгебры линейные элементы геометрических фигур представляются в виде векторов.

Пример 3. Найти длины сторон и углы треугольника с вершинами в точкахB A(−1;− 2; 4), B(−4;− 2; 0), C (3;− 2; 1).

A

γ

Рис. 38. Пример

Решение: представляем стороны треугольника в виде векторов (рис. 38) и находим координаты этих векторов:

r

(

(

)

(

)

)

(

)

AB = a =

−4

−

−

−2

; 0

− 4

=

−3;0;−

4

;

−1 ; − 2

v

(

(

)

(

)

)

(

)

AC = c =

3

−

−

−2

; 1

− 4

=

4;0;− 3

;

−1 ; − 2

BC = b =

(

)

7; 0; 1 .

uuuur

(−3)2 + 02 + (−4)2 = 5,

Найдем длины этих векторов:

AB

=

= 5

AC

= 5;

BC

2 .

Определяем углы между сторонами:

128

r r

v

r

(−3) 4

+ 0 0 +

(

−4) (−3)

π

a

c

cosα = cos(a,c) =

r

r

=

= 0;

α =

.

5 5

a

c

2

r

r

7 4 + 0 0 +1

(

−3

)

1

cosβ = cos(b

,c)=

=

β = π .

5 5

2

2

4

По теореме о сумме углов треугольника должно быть γ = π .

r

(

−3

)

7 + 0 0 +

(

−4

)

1

4

r

1

Проверим: cos(a,b)=

= −

;

cosγ =

5 5

2

2

r

r

7 4 + 0 0 +1

(

−3

)

1

= cos(π − (a,b ))= −

=

(см. рис. 38).

55

2

3.6.20. Определение координат (проекций) вектора

при изменении системы координат

r

= (a1,a2,a3 )

Пусть задан вектор a

в некоторой (старой) пря-

моугольной

системе координат Oxyz. Необходимо определить

r

(

1

2

3 )

координаты того же вектора a =

в новой системе ко-

a′, a′ ,

a′

ординат Ox′y′z′.

Пусть начала координат в обеих системах совпадают. Это не уменьшает общности получаемых результатов, так как параллельный перенос вектора не изменяет его проекций (координат).

Вектор a в двух системах координат имеет вид

r	v	+ a j + a k ;		r	= a′i′ + a′ j′ + a′ k′.
a	= a i			a
	1	2	3		1	2	3

r

r

r

r

r

r

r

r

r

r

r

r

a1′ = a

i′ = (a1i

+ a2 j + a3k ) i′ = a1 (i

i′)+ a2 ( j

i′)+ a3 (k

i′);

a1′ = α11a1 + α12a2 + α13a3 ,

где

r

r r

r

r

r ur

r

r

r r

r

α11 = i

i′ = cos

(i ,i′), α12 =

j

i′

= cos(i , j′), α13

= k

i′ = cos(k,i′).

Аналогично получаем:

a2′ = α21a1 + α22a2 + α23a3 ;

a3′ = α31a1 + α32a2 + α33a3 .

Эти формулы можно представить в матричной форме:

129

Рис. 39. Переход к новым координатам

a1′			α11			α12		α13		a1
a′		=		α	21	α	22	α	23	a	.
2				α		α		α		2
a′					31		32		33	a
3										3
Или,					более			коротко:			a′ =

= (αik )a.

Пусть на плоскости даны две различные прямоугольные системы координат XOY и X ′O′Y′и дан вектор a, координаты кото-

рого в системе XOY известны. Требуется найти координаты того же вектора в системе X ′O′Y′.

Теорема (о переходе к новым координатам)

Пусть координаты произвольного вектора a в системе XOY

равны	a , a , а в системе		X ′O′Y′ – a′, a′		тогда если система
	1	2	1	2
X ′O′Y′	получена из системы XOY поворотом на угол α вокруг

точки О против часовой стрелки, то

x = x′cosα − y′sin α;

y= x′sin α + y′cosα.

Втензорном исчислении, которое находит наиболее широкое применение в механике сплошной среды (гидромеханике, теории упругости и т.д.) закон преобразования координат лежит в основе определения вектора, который считают тензором первого ранга.

	3.70. Векторное произведение векторов
	Определение: векторным произведением вектора a на вектор
b	r	r
	называется вектор c	= a b , удовлетворяющий условиям:

130

1) Длина вектора c

равна про-

изведению длин векторов a и b на

синус

угла

между

ними:

r

=

c

=

r

b

sin α.

a

2) Линия

действия

вектора

c

перпендикулярна линиям действия

векторов a и b .

3) Вектор c направлен так, что

Рис. 40. Векторное

наблюдатель, смотрящий с конца

произведение

вектора c , видит поворот от век-

тора a к вектору b

на наименьший из двух возможных углов,

происходящим против часовой стрелки

Теорема

(свойства векторного произведения)

r

r

имеют место тождества:

Для любых векторов a,b,c

1)

r

r

(от перестановки

множителей меняется

a×b = −(b × a)

знак произведения);

r

r

2) Для любого числа A верно: (Aa)×b = A(a ×b).

r

r

r

r

r

3) (a + b )× c

= a × c

+ b × c .

Теорема

(векторное произведение в координатах)

r

(a1,a2,a3 )

и b = (b1, b2,b3) ,

Если a =

r

то a ×b = (a2b3 − a3b2 , a3b1 − a1b3, a1b2 − a2b1).

Замечание. Для запоминания и вычисления координат векторного произведения используют определитель

rr

i j k a1 a2 a3 ,

b1 b2 b3

и его разложение по первой строке

131

r

r

i

j

k

r

a2

a3

r

a1

a3

r

a1 a2

=

a a a

= i

− j

+ k

1

2

3

b2

b3

b1 b3

b1 b2

b1

b2

b3

r

r

r

= i (a2b3 − a3b2 ) + j(a3b1

− a1b3 ) + k (a1b2

− a2b1),

т.е. коэффициенты при векторах i ,

j, k

будут равны соответствующим

r

r

координатам вектора c

= a×b .

Теорема

(двойное векторное произведение)

Для

любых векторов

a,

b ,

c

имеет

место тождество

r

r

r

r r

r

−

r r

r

a

×(b×ñ)

= b(a

ñ)

ñ(a

b).

Даны

векторы

r

b = (−3 ;4; 1);

Пример.

a = (2; 0; − 5);

r

r

r

r

r

r

c

= (0; 5; −1). Найти a×b, b

× a ,

(a ×b)×c .

i

j

k

r

r

r

r

Решение:

1)

2

0

−5

,

=

= 20i +13 j

+ 8k

значит, a ×b

−3

4

1

= (20, 13, 8);

r

r

2) b× a

= −a ×b = (−20, −13,−8);

i

j

k

r

r

r

r

r

r

(−53,20,100).

3)

20

13

8

= −53i + 20 j +

100k .

(a× b)× c

=

0

5

−1

3.7.10. Геометрические приложения векторного произведения

1)Модуль векторного произведения двух векторов a и b равен площади параллелограмма, построенного на этих векторах как на сторонах.

2)Если векторы a и b коллинеарны, то условие коллинеарно-

r

сти в векторной форме имеет вид a × b = 0.

132