scherbo-sp2

локна сохраняют свою первоначальную длину, их относительные удлинения и укорочения равны нулю (εz = 0). Поэтому в поперечных сечениях стержня возникают лишь касательные напряжения, а нормальные отсутствуют.

В п. 5.5 М-5 было установлено, что при кручении полосы, имеющей прямоугольное сечение, поток касательных напряжений в поперечном се- чении направлен по замкнутым кривым, как показано на рис. 12.4, а. На рис. 12.4, б показана соответствующая эпюра касательных напряжений.

Рис. 12.4

Максимальные напряжения возникают в точках, лежащих в середине длинной стороны у грани сечения, и определяются следующей формулой:

		τ	max	=		M 0		δ.	(12.1)
						Jd
Угол закручивания полосы находится из выражения
			′		M 0			.	(12.2)
			Θ =		GJd
В формулах (12.1) и (12.2) обозначены:
М0 –		момент чистого кручения;
δ –	толщина поперечного сечения;
G –		модуль сдвига;
Jd	–	геометрическая характеристика сечения,							выполняющая ту же

роль, что и полярный момент инерции для стержней с круглым попереч- ным сечением. Эта характеристика для узкой полосы

			=	hδ3
	J	d			.	(12.3)
				3

В стержнях, состоящих из нескольких узких полос прямоугольного сечения, поток касательных напряжений направлен также по замкнутым кривым (рис. 12.4, в). С достаточной для практики точностью можно счи- тать, что в таких профилях поток касательных напряжений состоит из ряда замкнутых контуров, как это показано для двутавра на рис. 12.4, г.

При этом распределение напряжений по толщине сечения принима- ется по линейному закону (рис. 12.4, д). Таким образом, на средней линии

101

элементов сечения касательные напряжения равны нулю. Максимальное значение напряжения приобретают в элементах с наибольшей толщиной δ и в точках, наиболее удаленных от средней линии и расположенных посе- редине длинных сторон элемента. Формула для определения τmах имеет тот же вид, что и (12.1), но величина Jd в ней, а также и в формуле (12.2) в данном случае вычисляется по формуле

	n	h δ3
	Jd = α∑	i i	,	(12.4)
		3
	i−1
где hi –	длина каждой части, измеряемая по средней линии;
δi –	толщина той же части.

Коэффициент α в формуле (12.4) по данным опыта принимается рав- ным для прокатных профилей:

∙двутавра – 1,20;

∙швеллера – 1,12;

∙уголка – 1,0.

Для сварного двутавра с ребрами жесткости α = 1,5.

Для профилей, составленных из прокатных двутавров, швеллеров или уголков, соединенных между собой не более чем одним рядом заклепок или сварным швом по одной кромке, величина Jd определяется как сумма:

						′	′′	′′′	+ ...,	(12.5)
		′	′′	′′′		Jd = Jd	+ Jd	+ Jd
	где				–	значения характеристик,			вычисляемых	для отдельных
		Jd	, Jd	, Jd

профилей по формуле (12.4).

12.3. Стесненное кручение и его особенности

Стесненным кручением называется такое кручение, при котором де- планация в различных поперечных сечениях неодинаковая.

Если, например, тонкостенный стержень цилиндрической формы (см. рис. 12.3, а) жестко заделать на одном конце, а к другому приложить закручивающий момент, то сечение в заделке останется плоским (депла- нация равна нулю), на свободном же конце депланация сечения будет наибольшей. В промежуточных сечениях депланация изменяется по неко- торому закону от нуля на заделанном конце до наибольшей на свободном конце. Так как перемещения точек разных сечений по длине различны, то появятся относительные удлинения волокон ( ez ¹ 0 ) и в поперечных сече- ниях стержня возникнут не только касательные, но и нормальные напря- жения.

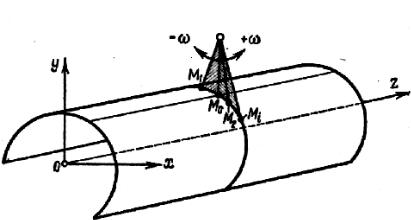
Для изучения основных особенностей стесненного кручения рас- смотрим двутавр, жестко заделанный одним концом в стену.

На рис. 12.5, а изображена срединная поверхность такого двутавра.

102

а)	z	б)			z
				y
Mz					Mz
Т	-σω				+σω
Nω			Nω		x
Nω	+σω				-σω
				Nω

	в)	dF
Т	σω
		δ
	Рис. 12.5

Представляя Mz в виде пары сил Т, нетрудно установить, что под действием этих сил одновременно с закручиванием двутавра происходит и изгиб его полок в противоположных направлениях.

Разрежем мысленно двутавр в каком-либо поперечном сечении и от- бросим его часть, к которой приложены силы Т. Эпюры нормальных на- пряжений в сечении оставшейся части двутавра имеют вид, показанный на рис. 12.5, б. Обозначим эти напряжения через σω и будем считать, что они одинаковы по толщине полки δ ввиду ее малых размеров (рис. 12.5, в).

По напряжениям σω можно определить четыре равные силы Nω, обра- зующие самоуравновешенную систему внутренних сил, возникновение ко- торой является одной из главных особенностей стесненного кручения. Эти силы не могут быть определены из условий равновесия рассматриваемой части двутавра. Из условия равновесия отсеченной части можно устано- вить, что для данной системы сил должны удовлетворяться равенства:

M x = ∫
	(σωdF ) y = 0;
F
M y = ∫			(12.6)
	(σωdF ) x = 0;
F
N = ∫ σωdF = 0,
F

т. е. изгибающие моменты относительно обеих главных осей инерции се- чения и продольная сила должны быть равны нулю.

В поперечном сечении возникают также касательные напряжения. Так как в исследуемом случае одновременно имеют место как деформа- ции кручения, так и деформации изгиба, то, следовательно, в сечениях стержня возникнут две системы касательных напряжений, соответствую- щих указанным деформациям.

103

К первой из них относятся напряжения, которые распределяются в сечении по закону свободного (чистого) кручения. Обозначим эти напря- жения τ0, а соответствующий им момент, называемый моментом чистого кручения, – М0. Последний можно представить себе как сумму моментов элементарных пар, составляющими которых служат касательные усилия, возникающие в сечениях стержня (рис. 12.6, а). Определение напряжений τ0, а также и соответствующего угла закручивания выполняется по форму-

лам (12.1) и (12.2).

Рис. 12.6

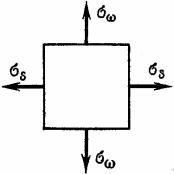
Касательные напряжения, относящиеся ко второй системе, которые обозначим через τω, возникают в связи с тем, что нормальные напряжения в поперечных сечениях стержня неодинаковы.

Направления напряжений τω в полках двутавра будут взаимно про- тивоположны (рис. 12.6, б), им соответствует момент, который называется изгибно-крутящим моментом и обозначается через Мω. Этот момент и момент М0 создают в сечении стержня внутренний крутящий момент Мкр, который уравновешивает момент внешних сил Мz.

Таким образом, внутренние силы в поперечных сечениях стержня при стесненном кручении приводятся к самоуравновешенной системе нормальных усилий, связанных с напряжениями σω, к моменту чистого кручения М0 и к изгибно-крутящему моменту Мω.

При этом условия равновесия для любой части стержня (рис. 12.5) дают единственное уравнение, которое устанавливает связь между внешними и внутренними силами:

M z = M кр = M 0 + M ω.

(12.7)

Отсюда следует, что для определения внутренних сил требуются дополнительные уравнения, составление которых осуществляется так же, как и для статически неопределимой задачи, на основе исследования уп- ругих деформаций стержня.

В связи с тем, что при стесненном кручении имеет место изгиб от- дельных элементов стержня, этот вид кручения называют также изгибным кручением.

104

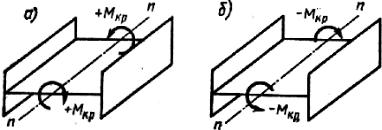
Установим правило знаков для крутящего момента. Крутящий мо-

мент Мкр в рассматриваемом сечении стержня будем считать положи- тельным, если при взгляде на сечение со стороны его внешней нормали видим момент, направленный по ходу часовой стрелки (рис. 12.7, а), и отрицательным, если тот же момент направлен против хода часовой стрелки (рис. 12.7, б).

Рис. 12.7

12.4.Зависимости между деформациями стержня

иперемещениями его точек

При построении теории расчета тонкостенных стержней на кручение принимаются две основные гипотезы. Первая из них состоит в том, что

деформации сдвига срединной поверхности стержня принимаются рав- ными нулю.

Иными словами, полагается, что угол между двумя прямыми, одна из которых совпадает с образующей срединной поверхности, а другая ей пер- пендикулярна, не изменяет своей величины при закручивании стержня.

По второй гипотезе, профиль поперечного сечения считается же-

стким, или недеформируемым. Под этим понимается условие, что проек- ция поперечного сечения на плоскость, перпендикулярную оси стержня, в процессе деформации сохраняет постоянные размеры и форму.

В соответствии с этой гипотезой деформацию стержня можно пред- ставить как совокупность поворотов поперечных сечений на определенный угол вокруг некоторого полюса, при которых каждое поперечное сечение одновременно будет испытывать депланацию.

Для исследования упругих деформаций рассмотрим стержень с произ- вольным очертанием поперечного сечения, находящийся в условиях стес- ненного кручения. Так как напряжения σω одинаковы по толщине сечения δ (см. рис. 12.5, в), то достаточно определить их для точек срединной по- верхности. Для этого необходимо исследовать перемещения точек, лежа- щих на срединной поверхности стержня, которая изображена на рис. 12.8.

Оси oу и oх приняты совмещенными с главными центральными ося- ми инерции сечения, а ось oz – с осью стержня.

105

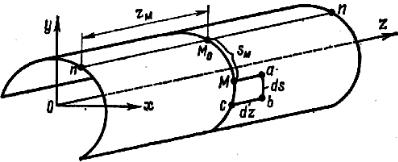
Рис. 12.8

Возьмем на срединной поверхности произвольную точку М и выде- лим около нее элементарную площадку, одна сторона которой является элементом дуги ds, а другая, перпендикулярная ей, – dz. Положение точки М определится координатой zM и дугой sM, которая отсчитывается от неко- торой начальной точки М0 на средней линии поперечного сечения, прохо- дящего через исследуемую точку М. Кроме этого, положение точки М оп- ределяется координатами хМ, yM и zM.

Общее перемещение элементарной площадки можно представить со- стоящим из поступательного перемещения и поворота вокруг точки М.

Обозначим перемещение точки М по образующей, т. е. вдоль оси оz, через u, а по касательной к дуге s – через v. Очевидно, что каждое из этих перемещений является функцией координат z и s точки:

u = f1		(z, s);	(а)
v = f	2	(z, s).

Обе функции (а) должны быть непрерывными, так как в процессе упругих деформаций цельность стержня не может быть нарушена.

При поступательном перемещении (рис. 12.9, а) ребро Ма, равное dz, получит удлинение dz, которое в то же время будет и приращением функции u. Так как при переходе от точки М к точке а изменяется на dz только одна координата z, а другая s остается без изменения, то прираще- ние данной функции зависит от одной частной производной

		dz = ∂u dz.		(б)
			∂z
Отсюда относительное удлинение ребра Ма равно
ε	z	=	dz = ∂u .	(12.8)
			dz ∂z

Ребро площадки ds не получит приращения, так как оно совпадает с профилем поперечного сечения, который согласно второй гипотезе считает- ся недеформируемым. Поэтому соответствующее удлинение равно нулю:

εs = 0.

(12.9)

Исследуем теперь поворот площадки около точки М.

106

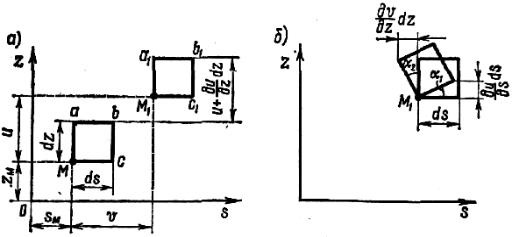
Рис. 12.9

Согласно первой гипотезе об отсутствии сдвигов в срединной по- верхности поворот площадки произойдет без искажения прямых углов ме- жду ее ребрами (рис. 12.9, б).

Отсюда следует равенство углов:

α1 = α2.

(12.10)

Приращения функций u и v равны:

u =	∂u ds;
	∂s
v = − ∂v dz.
	∂z

	Из рис. 12.9, б видно, что			∂u ds
	α ≈ tgα =			∂s			;
	1	1			ds
					−	∂v dz
	α2	≈ tgα2	=			∂z
								.
						dz

Или согласно равенству (12.10)

∂u = − ∂v . ∂s ∂z

(в)

(г)

(12.11)

В равенство (12.11) входят две неизвестные функции u и v, которые необходимо определить. Пусть поперечное сечение при закручивании стержня повернулось вокруг некоторого полюса А (рис. 12.10, а) на угол Θ.

Условимся считать положительным такой угол закручивания Θ, при ко- тором сечение поворачивается против хода часовой стрелки, если смот- реть на него из начала координат в положительном направлении оси z.

107

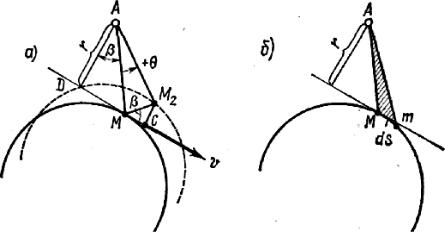
Рис. 12.10

В соответствии с гипотезой о недеформируемости профиля сечения последнее повернется как жесткий диск, при этом точка М перейдет в по- ложение М2. По малости угла Q примем, что

ММ2 = АМQ.

(12.12)

Проведем касательную в точке М и обозначим расстояние полюса до касательной через r, а угол ÐMAD – через b. Проектируя перемещение точ- ки М на касательную, получим

	MC = v = MM 2 cosβ,						(д)
	или с учетом равенства (12.12)
	v = AM (cosβ)Θ.						(е)
	Имея в виду, что AM cosβ = r, найдем
	v = Θr.						(12.13)
	Частная производная функции v по z с учетом того, что r не зависит
	от z, запишется в виде
	∂v =	∂Θ r.					(12.14)
	¶z	¶z	∂Θ
	В дальнейшем примем обозначения			= Q¢,	¶2Q		= Q¢¢ и т. д.
			¶z		¶	2
					z
	Тогда
	∂v = Q¢r.						(12.15)
	¶z	∂v в равенство (12.11), найдем
	Подставляя найденное значение
		¶z
	∂u = -Q¢r.						(12.16)
	¶s
	108

Для получения функции u выполним интегрирование уравнение (12.16) по дуге s, учитывая, что Θ'от дуги s не зависит. В результате имеем

u = ∫	∂u ds = −Θ′∫rds + u0 (z).		(12.17)
s	∂s	s

Так как здесь интегрировалась частная производная от u, то в пра- вую часть выражения (12.17) введена функция u0(z), не зависящая от s. По своему физическому смыслу функция u0(z) выражает некоторую часть перемещения u, которая одинакова для всех точек сечения.

Произведение rds в уравнении (12.17) является удвоенной площадью элементарного сектора АМm, показанного на рис. 12.10, б, Обозначая эту

площадь через dω, получим

∫rds = ∫dω = ω.

s	s
Тогда уравнение (12.17) запишется в следующем виде:
	′	(z),	(12.18)
	u = −Θ ω + u0

где ω определяет собой удвоенную площадь, например, сектора АМ0М1 (рис. 12.11), образованного при вращении радиуса вектора AM0 по ходу ча- совой стрелки вокруг полюса А. Величину ω называют секториальной площадью. Конец радиуса вектора при образовании ω перемещается по профилю сечения от начальной точки М0. Как видно, значение ω для раз- личных точек профиля зависит от расположения полюса А и точки М0.

A

Рис. 12.11

Так, например, значение ω, соответствующее точке М1, определится, как уже показано выше, сектором АМ0М1, точке М2 – сектором АМ0М2, а любой точке Мi – сектором АМ0Мi.

Секториальную площадь ω считают положительной, если при дви- жении точки по профилю сечения от начала отсчета М0 соответствующий радиус-вектор вращается против хода часовой стрелки при взгляде на се- чение в положительном направлении оси z.

109

Так, для точки М1 (см. рис. 12.11) ω имеет отрицательный знак, а для точек М2 и Мi – положительный.

Всвязи с тем, что для каждой точки профиля секториальная площадь

ωимеет свое определенное значение и знак, она называется секториальной координатой точки.

Беря частную производную функции u (12.18) по z с учетом того, что

ωот координаты z не зависит, и подставляя в равенство (12.8), получим

′′	′	(12.19)
εz = −Θ ω + u0 z.

Зависимости (12.9) и (12.19), найденные в результате анализа упру- гих деформаций стержня, служат теми дополнительными уравнениями, которые позволяют вместе с уравнениями статики установить закон рас- пределения и величину напряжений, а также и соответствующих им внут- ренних силовых факторов при стесненном кручении.

12.5. Закон распределения нормальных и касательных напряжений в сечении стержня

Рассмотрим элементарную площадку, выделенную в окрестности произвольной точки М срединной поверхности (рис. 12.12).

Допустим, что при стесненном кручении, так же как при изгибе и свободном кручении, отсутст- вует взаимное давление между продольными во- локнами, т. е. σs = 0.

Исходя из указанного допущения, согласно закону Гука

		σω = Eεz .		(12.20)
Подставляя вместо εz его значение из (12.19),
получим		′′	′
Рис. 12.12	σω
		= −EΘ ω + Eu0 (z).		(12.21)
	′	используем	третье	из равенств
Для определения функции u0 (z)
(12.6). Вводя в него значение σω из (12.21), имеем
N = ∫ σωdF =	′′	′	= 0.	(12.22)
	∫[−EΘ ω + Eu0 (z)] dF
F	F

	′′	и	′	(z)	не зависят от дуги
Имея в виду, что функции Θ			u0
ние (12.22) можно записать в таком виде:
′′			′
−EΘ ∫	ωdF + Eu0 (z) ∫ dF = 0.
F				F

s, выраже-

(12.23)

110