2FwlpVopmE

Выразим постоянные интегрирования C1,C2 ,C3 , являющиеся проек-

циями удвоенной секторной скорости C3 на оси координат. Вектор удвоен-

ной секторной

скорости

направлен

по нормали к плоскости орбиты

(рис. 13). Численно C3 равно

2

a2 1

e2

, но

C

3

P

P2

M

m

2

4

, и P

2 a

a

, тогда

a3

G

G M

m

p .

C3

k

Так как C1,C2 ,C3 – проекции C3 , то

C1

C3 cos

n, x

n, y .

C2

C3 cos

C3

C3 cos

n, z

Согласно рис. 13.

					Рис. 13
cos	n, x	sin	cos	900 i
cos	n, y	sin	900	cos	900 i .
cos	n, z	cos i

51

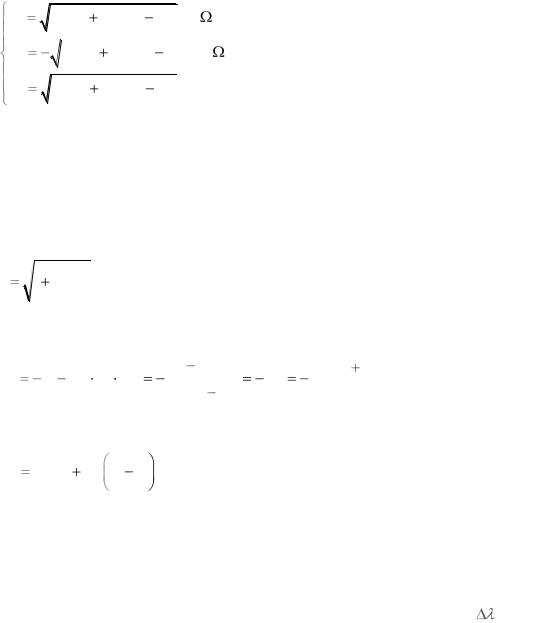
Тогда постоянные C1,C2 ,C3 равны

C	G M			m a 1	e2 sin				sin i
1
C2		G M		m a 1	e2			cos	sin i ,
C	G M			m a 1	e2		cos i
3

т.е. постоянные C1,C2 ,C3 выражены через элементы орбит спутника

(планеты).

Определим постоянную C4 . Для этого рассмотрим выражение для эксцентриситета

				2
	C C
e 1	4		3
	k 4

и выразим отсюда постоянную C4 .

C4

1 e2

k 4

1

1 e2 k 4

k 2

G M m

,

C 2

k 2a 1 e2

a

a

3

и подставим в интеграл энергии (2.7):

V 2	G M m	2	1		(2.16)
		r		a

Это уравнение определяет скорость, которую нужно придать спут-

нику для его полѐта по определѐнной заранее орбите. Это же уравнение позволяет определить орбиту ИСЗ в любой момент его движения. С помо-

щью радиолокации определяется расстояние r , а по смещению – дли-

ны волны на которой принимается его радиопередача, определяется ско-

рость движения спутника, тогда из этого уравнения находим a , т.е.

параметр орбиты спутника. Если она отличается от рассчитанной траекто-

рии, то осуществляется коррекция его движения. Именно это уравнение позволяет определить основные космические скорости спутников.

Для того чтобы спутник двигался по круговой орбите, ему необхо-

димо сообщить скорость:

52

V	G M m	, r a .
кр	r

Для того чтобы спутнику освободиться от центрального тела с ми-

нимальной скоростью необходимо сообщить спутнику параболическую скорость:

Vп 2Vкр , a .

Если же спутнику сообщить ещѐ большую скорость, то орбита будет гиперболической. Теперь, если движение спутника происходит под дейст-

вием притяжения нескольких тел, то решающим будет то тело, притяжение которого наибольшее, а притяжение других тел будут только возмущаю-

щими. Этим определяется сфера притяжения данного тела. Как только притяжение этого тела становится меньше, чем притяжение других тел, то спутник переходит в сферу притяжения другого тела. Например, круговая скорость на поверхности Земли определяет первую космическую скорость

	VI		GM		,	(2.17)
			R

где M , R – масса и радиус Земли.

Подставляя численные значения величин, входящих в (2.17) для пер-

вой космической скорости, получим 7,9 км/с.

Параболическая скорость в этих условиях – вторая космическая и

она равна:
VII	2VI ,	(2.18)

и еѐ численное значение равно 11,2 км/с. В этом случае спутник удалится от Земли и перейдет в сферу действия другого притягивающего централь-

ного тела.

Рассматривают ещѐ так называемую третью космическую скорость,

когда рассчитывают условия выхода спутника из пределов солнечной сис-

темы.

53

При условии, если спутник запускать в направлении движения Зем-

ли, имеющей орбитальную скорость движения относительно Солнца рав-

ную 30 км/с, то для того, чтобы выйти из сферы притяжения Земли двига-

ясь по параболической орбите относительно Солнца надо сообщить

скорость VIII равную 16,8 км/с.

Выразим постоянную интегрирования C5 , используя первый (обоб-

щѐнный) закон Кеплера (2.12).

r	p		,
	1 e cos	c5

при прохождении перигелия r min , значит рис. 14.

Рис. 14

cos	n	C5 1
n	C5	0	,
	C5
n
C5
где – долгота перигелия, тогда (2.12) перепишется:
r		p		,
	1 e cos
и введѐм новую переменную – истинную аномалию					, которая от-
считывается от перигелия рис. 15,

54

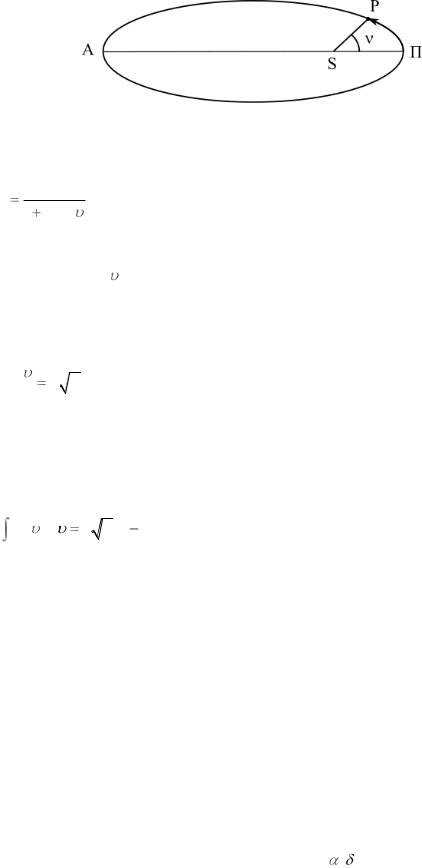
Рис. 15

тогда

	p
r	1 e cos .	(2.19)

Так как движение по орбите на основании второго закона Кеплера неравномерное, то меняется не пропорционально времени, и для того,

чтобы его определить, как функцию времени необходимо было бы решить уравнение:

	r2d
		k p .			(2.20)
	dt

При интегрировании этого уравнения надо знать, как радиус орбиты зависит от угла эксцентрической аномалии. Формальное интегрирование позволяет выразить ещѐ одну постоянную интегрирования C6 :

r2						,
	d	k p t t			0

т.е. C6 определяется моментом прохождения спутником перигелия.

Основные задачи небесной механики

Небесная механика в вопросах определения поступательного движе-

ния небесных тел решает две основные задачи:

1.Определение элементов орбит из наблюдений.

2.Вычисление эфемерид, то есть таблиц координат небесных тел в оп-

ределѐнные моменты времени.

Для определения элементов орбит необходимо из наблюдений опре-

делять экваториальные координаты светила , . Для шести элементов

орбит необходимо не менее трѐх наблюдений на достаточно большом уда-

55

лении друг от друга. Практически всегда производится определѐнная сис-

тема наблюдений, которая затем усредняется. Следовательно, получают три средних места положений.

Определение эфемерид основано на знании элементов орбит светил и известных законов движения спутников относительно центрального тела.

Первоначально определяются координаты спутника в плоскости орбиты

(2.19):

	p
r		.
	1 e cos

Для определения , которое изменяется неравномерно, согласно второго закона Кеплера, введѐм две вспомогательные аномалии. Пусть

n	2	– угловая скорость движения спутника. Если бы движение было бы
	P

равномерным, то тогда угол поворота спутника, отсчитываемый от периге-

лия, равнялся бы:

M n t t0 ,

(2.21)

который и есть средняя аномалия.

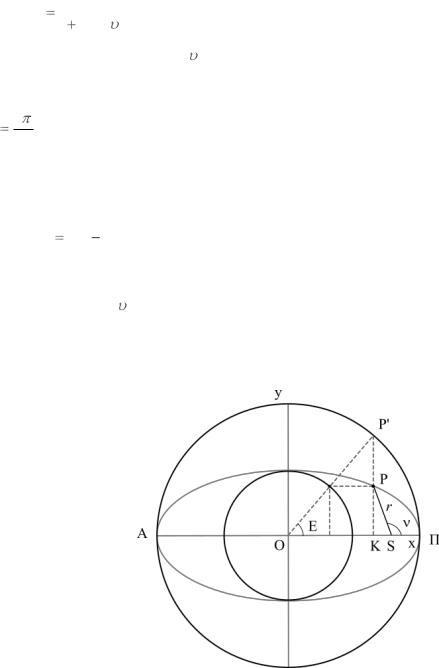
Каждому соответствует центральный угол, который называется эксцентрической аномалией рис.16., т.е. E – центральный угол, опреде-

ляющий положение спутника на орбите.

Рис. 16

56

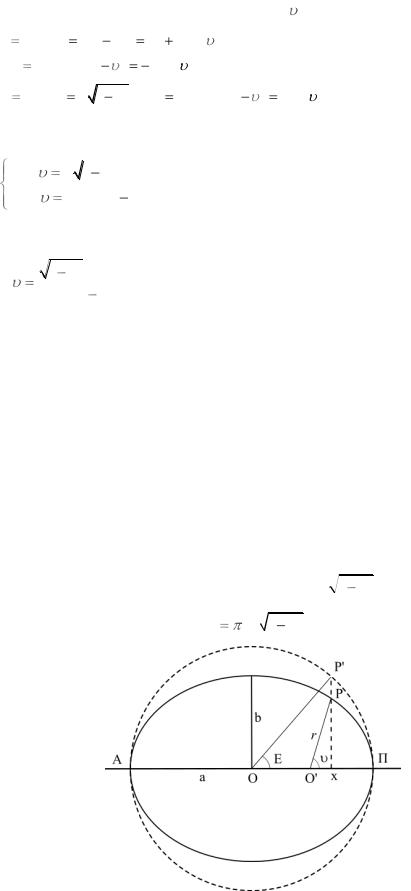
Определим зависимость между E и :

x

a cos E

OS

KS ae

r cos

KS

r cos 1800

r cos

,

y

b sin E

a 1 e2 sin E

r sin 1800

r sin

тогда

r sin

a

1

e2 sin E ,

r cos

a cos E e

отсюда

tg

1

e2 sin E

.

(2.22)

cos E

e

Следующий шаг – это нахождение связи между эксцентрической и

средней аномалиями. Этот шаг и завершает цепочку последовательных со-

отношений, чтобы решить задачу определения эфемерид спутника при его движении относительно центрального тела. Как известно, финитное дви-

жение небесных тел в Солнечной системе происходит по эллипсу. Однако,

если необходимо установить, в какой точке небесное тело находится в за-

данный момент времени, этой информации недостаточно и надо восполь-

зоваться уравнением Кеплера.

Эллипс – это сплюснутая на величину 1 e2 окружность. Действи-

тельно, площадь эллипса равна S a2 1 e2 (рис. 17).

Рис. 17

57

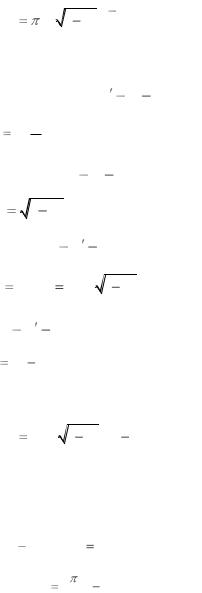
Согласно второму закону Кеплера, который гласит, что площадь, за-

метаемая радиус вектором небесного тела пропорционально времени,

можно записать:

		a2			t t0	(2.23)
	S t		1 e2
					P

Для вычисления площади S рассмотрим вспомогательные фигуры:

сектор окружности P O П

S1 a2 E2 ,

	сектор эллипса P O										П
	S	2		1 e2 S ,
						1
	треугольник O						O		P
			1				1
	S	3		yae				a2	1		e2 sin E ,
			2			2

сектор P O П

S S2 S3 ,

отсюда, площадь S равна:

		1
S t			a2		1		e2 E e sin E .
	2
Сравнивая это выражение с ранее выведенным выражением из вто-
рого закона Кеплера, получаем:
E t	e sin E					t	M t ,		(2.24)
где M t				2			t t0 .
					P
Заметим,					что это трансцендентное уравнение относительно E				и по-
лучить явное решение в общем случае не удаѐтся.

Для вычисления координат небесного тела необходимо найти экс-

центрическую аномалию по известным M и e , а затем определить радиус-

вектор и угол и. если необходимо x и y по приведенным выше формулам.

Интересным вопросом остаѐтся нахождение методов решения урав-

нения Кеплера. Этим занимались лучшие умы человечества на протяжении

58

последних четырѐхсот лет. Результатом было обогащение математики множеством интересных идей.

Задача Кеплера часто используется для проверки систем математи-

ческого моделирования, как очень хорошо изученная и вместе с тем про-

стая. Вместе с задачей о гармоническом осцилляторе - это одна из двух за-

дач о движении тела по замкнутой траектории, когда тело возвращается в исходную точку с той же самой скоростью. Задача Кеплера используется для построения новых методов классической механики, в частности Га-

мильтонова формализма, уравнения Гамильтона-Якоби и системы пере-

менных «действие-угол».

Решить уравнение Кеплера, с заданной точностью, можно методом

последовательных приближений (метод итераций):

En	Mn	esin En 1 ,
E0	0, E1	M1,...

Последовательность определения полярных координат спутника для вычисления эфемерид будет:

1.Задаѐм моменты времени t1,t2 ,t3 ,...

2.Вычисляем M1, M2 , M3 ,...

3.По уравнению Кеплера находим E1, E2 , E3 ,...

4.	Из (21)	получаем 1, 2 , 3 ,...
5.	Из (18)	вычисляем r1, r2 , r3 ,...

Зная координаты спутника в плоскости орбиты, можем вычислить

координаты относительно любой координатной системы, поворотом коор-

динатных осей. В частности, можно получить экваториальные координаты спутника. Таким методом вычисляются орбиты небесных тел для невоз-

мущѐнного движения. В случае возмущенного движения, то есть в случае действия других тел, необходимо будет в полученные координаты вводить соответствующие поправки.

59

Задачи к главе 2

Задача № 17

Найти значение истинной аномалии планеты, при которых еѐ ради-

ус-вектор равен среднему гелиоцентрическому расстоянию.

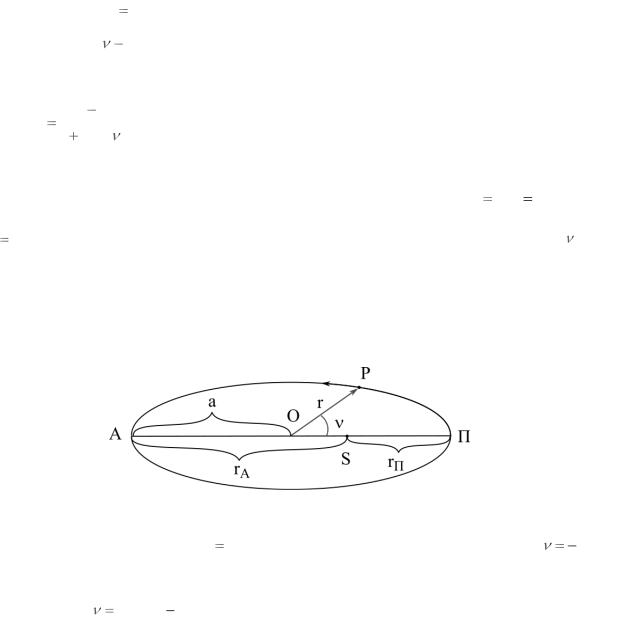
Данные: r a ;

Найти: ?

Решение: Воспользуемся третьим обобщѐнным законом Кеплера:

					a 1	e2
		r					.
					1 e cos
		Здесь,				на рис. 2.1(з),		r	– радиус-вектор, определяющий положение
	планеты P					на орбите, a		–	большая полуось орбиты ( АО OП АП / 2 ),
	e	OS		– эксцентриситет орбиты, задающий форму орбиты, и, наконец, –
		OП

истинная аномалия, угол, отсчитываемый от направления перицентра к по-

ложению планеты на орбите, с центром в фокусе эллипса, в котором нахо-

дится Солнце S .

Рис. 2.1(з)

Подставляя условие r a , находим следующее выражение: cos		e .
Это условие и даѐт ответ задачи.
Ответ:	arccos e .

Задача № 18

На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное рас-

стояние и эксцентриситет орбиты равны 0,187 а.е. и 0,827, а у Симеизы –

60