книги / Математическая логика и теория алгоритмов. Анализ алгоритмов

Рис. 4.2. Выбор режима отладки регистров

Появится окно регистров. Нажимая на кнопку шаг (слева на «Плеере»), производим отладку. Можно также вызвать окно регистров специальных функций (рис. 4.3) и внешнюю память при ее наличии.

Появляется также окно с программой, изображенное на рис. 4.4.

Рис. 4.3. Вызов окна регистров специальных функций

91

Рис. 4.4. Окно исходного кода

Далее переходим к пошаговому выполнению программы. Имеются специальные функциональные кнопки отладчика, кроме того, с помощью меню выбираются различные опции.

92

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1 АНАЛИЗ СЛОЖНОСТИ НЕРЕКУРСИВНЫХ АЛГОРИТМОВ

Цель занятия: приобретение навыков анализа сложности нерекурсивных алгоритмов и получения верхних, средних и нижних оценок сложности.

Контрольные вопросы

1.Что такое алгоритм?

2.Какие вы знаете способы записи алгоритма?

3.Каковы основные свойства алгоритма?

4.Какие характеристики используются для оценки алгоритма, насколько алгоритм применим на практике?

5.От чего зависит время работы алгоритма?

6.Что такое элементарная операция?

7.Что такое функция сложности алгоритма?

8. Что такое верхняя, нижняя и средняя оценки сложности? 9. Всегда ли для заданного алгоритма можно точно опре-

делить его функцию сложности?

Методика решения задач

Задача 1. Найти функцию сложности для процедуры умножения двух квадратных матриц размерности n*n. При оценке не учитывать затраты на организацию циклов for. Текст процедуры приведен ниже:

type

mas = array[1..n,1..n] of integer;

…

procedure mult(a,b:mas; var c:mas); var i,j,k:integer;

s:integer;

93

begin

for i:=1 to n do for j:=1 to n do begin

s:=0;

for k:=1 to n do s:=s+a[i,k]*b[k,j];

c[i,j]:=s end

end;

Решение. Для удобства запишем операторы в таблицу

	№		Строка программы	Кол-во операций
	строки
1			for i:=1 to n do	Не учитываем согласно заданию
2			for j:=1 to n do	Не учитываем согласно заданию
3			begin	Тоже не учитываем
4			s:=0;	1 присваивание
5			for k:=1 to n do	Не учитываем согласно заданию
	6		s:=s+a[i,k]*b[k,j];	3 (умножение, сложение и
				присваивание)
7			c[i,j]:=s	1 присваивание
8			end	Тоже не учитываем

Как описано в условии задания, затраты на организацию циклов for учитывать не будем, поэтому в строках 1, 2 и 5 нет учитываемых операций. В строках 3 и 8 операций, очевидно, тоже нет. В строке 4 выполняется 1 операция присваивания. Такую операцию мы считаем элементарной, а её сложность считаем равной 1. В строке 6 имеются 3 операции, которые мы считаем элементарными: одно умножение, одно сложение и одно присваивание. Наконец, в строке 7 одна элементарная операция – присваивание.

Теперь посчитаем, сколько раз выполняется каждая строка. Все строки с 4-й по 7-ю находятся внутри двух вложенных циклов (строки 1–2). Внешний цикл по i (в строке 1) выполняется n раз. При каждом значении i внутренний цикл по j

94

(в строке 2) выполняется тоже n раз. Таким образом, строки 4–7 выполняются n n = n2 раз.

Итак, операции в строках 4 и 7 выполняются n2 раз. Строка 6 находится внутри ещё одного цикла по k, который выполняется тоже n раз, то есть n2 повторений по n раз, итого: n2 n = n3 раз.

В итоге получаем следующую функцию сложности процедуры mult:

tmult (n) = 1 n2 + 3 n3 + 1 n2 = 3n3 + 2n2.

Такая функция имеет порядок роста O (n3). Визуализация алгоритма (задача 1) в виде схемы имеет вид (рис. 5.1).

Рис. 5.1. Схема алгоритма задачи 1

С использованием символов циклов получим схему алгоритма (рис. 5.2).

95

Рис. 5.2. Схема алгоритма задачи 1 с использованием символов циклов

Таким образом:

1.Любое последовательное соединение в схеме алгоритма (в том числе циклов) – сумма операций в этих блоках.

2.Вложенные циклы. В общем случае находим сумму числа итераций внутреннего цикла по всем значениям параметра внешнего цикла. В частном случае, если число итераций внутреннего цикла не зависит от значения параметра внешнего цикла, то по комбинаторному правилу умножения находим произведение числа итераций циклов.

Задача 2. Для процедуры, выполняющей «пузырьковую» сортировку одномерного массива размерности n, определить верхнюю, нижнюю и среднюю оценки сложности. Текст процедуры следующий:

96

procedure sort;

var temp,i,j:integer; begin

for i:=1 to n-1 do for j:=1 to n-i do

if M[j]>M[j+1] then begin

temp:=M[j+1];

M[j+1]:=M[j];

M[j]:=temp end

end;

Решение. Запишем операторы в таблицу

	№		Строка программы		Кол-во операций
	строки
1			for i:=1 to n-1 do
2			for j:=1 to n-i do
3			if M[j]>M[j+1] then		2 (сложение и сравнение)
4			begin
	5		temp:=M[j+1];		2 (сложение и
					присваивание)
	6		M[j+1]:=M[j];		2 (сложение и
					присваивание)
7			M[j]:=temp		1 присваивание
8			end

Количество операций в каждой строке определим, как и раньше: в строке 3 это 2 операции (сложение и сравнение),

встроках 5 и 6 – по 2 операции (сложение и присваивание),

встроке 7 – 1 операция присваивания.

Всилу наличия условного оператора в строке 3 нам действительно придётся анализировать худший, средний и лучший случаи. Для начала рассмотрим худший случай.

Ветка «then» в условном операторе содержит строки 5–7, в которых в сумме выполняется 2+2+1 = 5 операций. Ветка «else» отсутствует, то есть её сложность равна 0, потому что после неё следует end.

97

Таким образом, худшим случаем будут такие входные данные, когда выполнение алгоритма каждый раз идёт по ветке «then» (такое возможно, если на вход поступает массив, отсортированный в обратном порядке). Тогда на каждой итерации цикла будут выполняться все строки 3–7, общая сложность которых равна 7. Посчитаем, сколько раз выполнятся эти строки. Внешний цикл (в строке 1) выполняется n–1 раз. При фиксированном значении i внутренний цикл (в строке 2) выполняется n– i раз. Поскольку количество повторений внутреннего цикла зависит от параметра внешнего цикла, общее количество повторений посчитаем в виде суммы:

n 1

Kповт n i n 1 n 2 n n 1

i 1

n 1

n 1 n 2 ... 1 i.

i 1

Данная сумма представляет собой сумму всех натуральных чисел от 1 до n–1, которую можно найти по формуле суммы арифметической прогрессии:

n 1				1n2		1n.
Kповт i n (n		1)
i 1	2			2		2

В итоге получаем следующую верхнюю оценку сложности процедуры sort:

tsortmax (n) Kповт 7 72n2 72n ~ O(n2).

В лучшем случае, наоборот, выполнение алгоритма каждый раз идёт по ветке «else» (такое возможно, если на вход поступает массив, уже отсортированный в правильном порядке). Тогда на каждой итерации цикла будет выполняться только строка 3, сложность которой равна 2.

98

В итоге получаем следующую нижнюю оценку сложности процедуры sort:

tsortmin (n) Kповт 2 n2 n ~ O(n2).

Наконец, выполним оценку в среднем. Поскольку никаких дополнительных данных о вероятности появления тех или иных данных в условии нет, будем считать, что все данные равновероятны, и выполнение алгоритма в половине случаев идёт по ветке «then», а в половине – по ветке «else», то есть строка 3 выполняется всегда, а строки 5–7 – в половине случаев. Тогда средняя оценка сложности вычисляется следующим образом:

средн	(n) Kповт (2	1		1	n	2		1			9		9	n	2		9	n ~ O(n	2	).
tsort		2	5)	2				2	n		2		4				4

Можно заметить, что неравенство tmin (n) tсредн(n) tmax (n) ,

естественно, выполняется, но все три функции имеют одинаковый порядокроста O (n2).

Задача 3. Определить порядок роста функции сложности для процедуры бинарного поиска в упорядоченном одномерном массиве размерности n. Будем считать, что массив объявлен глобально, его имя M. Искомый элемент передаётся как параметр функции и называется elem. В качестве результата функция должна вернуть номер позиции искомого элемента, либо значение «–1», если искомого элемента в массиве нет. Суть бинарного поиска заключается в том, что на очередном шаге рассматривается элемент из середины массива. Если этот элемент меньше искомого, то дальше поиск продолжается только в правой половине массива (с учётом упорядоченности массива слева будут числа, которые еще меньше, поэтому их можно не рассматривать – рис. 5.3), иначе, наоборот, только в левой.

99

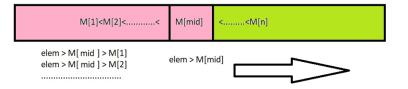
Рис. 5.3. Бинарный поиск в массиве

Текст процедуры приведен ниже:

function bin_find(elem:integer):integer; var mid,l,r:integer;

begin

l:=1; r:=n; while l<r do begin

mid:=(l+r) div 2; if elem>M[mid]

then l:=mid+1 else r:=mid

end;

if M[l]=elem

then bin_find:=l else bin_find:=-1

end;

Решение. Для удобства запишем операторы в таблицу

	№		Строка программы		Кол-во операций
	строки
1			l:=1; r:=n;		2 (два присваивания)
2			while l<r do		1 сравнение
3			begin
	4		mid:=(l+r) div 2;		3 (сложение, деление,
					присваивание)
5			if elem>M[mid]		1 сравнение
	6		then l:=mid+1		2 (сложение, присваивание)
	7		else r:=mid		1 присваивание
8			end;
9			if M[l]=elem		1 сравнение
10			then bin_find:=l		1 присваивание
11			else bin_find:=-1		1 присваивание

100