книги / Численные методы решения задач строительства. Ч. 1

1.3. Действия над матрицами

Действия над матрицами определяются с помощью действий над их элементами.

1.Сумма (разность) двух матриц одинакового типа

АВ есть матрица С того же типа:

С A B a b .
	ij	ij
2. Произведение матрицы		A aij	на число есть

матрица, элементы которой получены умножением всех

элементов на число : A a .
		ij
3. Произведением матрицы A aij				размером [m n]
на матрицу B b	размером [n r] называется матрица
ij

C c	размером [m r],	элементы которой вычисляются
ij
по формуле
		n
	cij	aik bkj .

k 1

То есть, чтобы получить элемент cij , надо вектор из

элементов i-й строки матрицы А скалярно умножить на вектор из элементов j-го столбца матрицы В.

Произведение А·В двух матриц в указанном порядке возможно в том и только в том случае, когда число столб-

цов матрицы А равно числу строк матрицы В.

Am n Bn r Cm r .

4. Произведение матрицы А на вектор X – частный случай произведения матрицы на матрицу, когда второй сомножитель является матрицей-столбцом (или вектором),

причем количество элементов вектора X должно быть обязательно равно количеству столбцов матрицы А. Резуль-

татом перемножения является вектор B , т.е. AX B, где

21

n

bi aij xj . j 1

Действия над матрицами подчиняются следующим зако-

нам:

1.А + В = В + А;

2.А + (В + С) = (А + В) + С;

3.(А + В)= А + В;

4.( А) = ( )А;

5.A(BC) = (AB)C;

6.(А + В)С = АС + ВС;

7.С(А + В) = СА + СВ;

8.(АВ) = ( А)В = А( В).

Основной особенностью матричного исчисления является некоммутативность произведения матриц:

АВ ВА,

т.е. произведение двух матриц не обладает свойством переместительности, и из существования произведения АВ вовсе не следует существование произведения ВА. Покажем это на примере.

Пример 1.1. Вычислить произведение двух матриц А и В.

		1 2			3	3		2	4
A B							2	1	3
			4	5
					6		4	3	0
1 3			2 2 3 4					1 2 2 1 3 3 1 4 2 3 3 0
	4	3 5 2 6 4						4 2 5 1 6 3				4 4 5 3 6 0
11			9	10
	46		31		.
					1

22

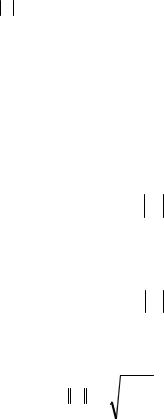
3		2	4		1		2	3	для данного случая не суще-
	2	1	3
B A
	4	3	0			4	5	6

ствует.

1.4. Нормы матрицы и вектора

Норма – это одна из важнейших скалярных характеристик векторов и матриц. Нормой произвольной матрицы А называется действительное число ||A||, удовлетворяющее условиям:

1. A 0, A 0, 0 0;

2. A A ;

3. A B A B.

Существуют различные способы определения нормы матрицы и вектора соответственно. В дальнейшем для анализа решений нам потребуется умение вычислятьэти нормы.

Матрица A aij может быть определена тремя нор-

мами:

норма 1 – максимальная сумма модулей элементов матрицы по строкам:

n

A1 maxi aij ; (1.7)

j 1

норма 2 – максимальная сумма модулей элементов матрицы по столбцам:

n

A 2 maxj aij ; (1.8)

i 1

норма 3 – корень квадратный из суммы квадратов всех элементов матрицы:

	n
A 3	aij2 .	(1.9)

i 1

23

Пример 1.2. Для матрицы А вычислить все три нормы

	3	2	4
	5	2
A			6
	0	7
			1

Решение:

А1 = max (3 + 2 + 4, 5 + 2 + 6, 0 + 7 + 1) = = max (9, 13, 8) = 13;

А 2 = max (3+5+0, 2+2+7, 4+6+1) = max (8, 11, 11) = 11;

A

3

32

22 42

52

22 62 72 12 144 12.

x

x 1

Для вектора

X

эти нормы вычисляются сле-

2

xn

дующим образом:

1 max | xi

| – максимальная по модулю координата

X

вектора;

x1

x2

xn

X

2

...

– сумма модулей координат

вектора;

3

x

2 x 2

... x

2

– корень квадратный из сум-

X

1

2

n

мы квадратов координат вектора.

1.5. Функции MS Excel

для операций над матрицами

Для выполнения операций с матрицами удобно использовать матричные функции MS Excel.

Категория: математические. Функции:

МУМНОЖ(<матрица1>;<матрица2>) – возвращает произведение матриц;

24

МОБР(<матрица>) – возвращает матрицу, обратную к данной;

МОПРЕД(<матрица>) – вычисляет определитель исходной квадратной матрицы.

Категория: ссылки и массивы. Функция: ТРАНСП(<матрица>) – транспонирует исходную пря-

моугольную матрицу, поворачивая ее относительно главной диагонали.

При выполнении операции следует:

Выделить блок, где будет размещен результат матричной операции.

В мастере функций выбрать нужную категорию

инужную функцию.

C помощью кнопки выделить исходную матрицу (бегущая пунктирная линия).

Одновременно нажать клавиши Shift+Ctrl+Enter.

Контрольные вопросы

1.Какие типы матриц вы знаете?

2.Определитель матрицы. Для всякой ли матрицы существует определитель? Какая матрица является вырожденной?

3.Обратная матрица. Для всякой ли матрицы существует обратная?

4.Произведение матриц. Всякие ли матрицы можно перемножать?

5.Что такое нормы матрицы (вектора)? Как они определяются?

6.Что такое транспонированная матрица?

25

ГЛАВА 2

Численные методы решения нелинейных уравнений

Решение некоторых строительных задач	сводится
к решению достаточно сложных нелинейных	уравнений.

В отдельных случаях они представляют собой самостоятельную задачу. Например, при проектировании очистных сооружений зависимости, связывающие проектные пара-

метры процесса очистки, являются чаще всего нелинейными. В других случаях решение нелинейных уравнений является составной частью более сложных задач, например частью расчета сооружения на устойчивость, и т.д.

Корни таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях и коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Следовательно, сама задача о точном определении корней уравнения теряет смысл, и важное значение приобретают методы приближенного нахождения корней уравнения и оценки степени их точности.

Нелинейные уравнения можно разделить на два класса: алгебраические и трансцендентные.

Алгебраические уравнения содержат только алгебраи-

ческие функции, например:
x2 5,4x 1,34 0,	x 1 0,8x 6,76 0.

Уравнения, содержащие любые другие функции (тригонометрические, логарифмические, показательные и др.), называются трансцендентными, например:

ex x 0, sin x ln 2,3x 0.

26

Любое нелинейное уравнение с одним неизвестным можно представить в общем виде:

f (x) = 0,

(2.1)

где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале A < x < B.

Всякое значение x*, обращающее уравнение (2.1) в тождество, называется корнем этого уравнения, т.е. f(x*) = 0.

С геометрической точки зрения задача нахождения корней уравнения (2.1) эквивалентна задаче нахождения нулей функции у = f(x), т.е. абсцисс точек пересечения графика функции c осью Х (значений xi, для которых выполняется условие f(xi) = 0 (для i = 1, 2,……)) (рис. 2.1).

y

					y = f(x)
		x*		x*		x*
		1		2		3
a							b	x

Рис. 2.1. Схема локализации корней

Исходя из специфики строительных задач будем рассматривать только действительные корни уравнения (2.1).

Методы решения нелинейных уравнений делятся на прямые (точные) и итерационные (приближенные).

Прямые методы позволяют записать корни уравнения в аналитическом виде, т.е. в виде некоторой формулы. На практике класс таких уравнений весьма невелик.

27

Итерационные (приближенные) методы – это методы последовательных приближений.

Алгоритм нахождения корней уравнения (2.1) с помощью итерационных методов складывается из двух этапов.

Первый этап – отделение или локализация корней. На этом этапе необходимо решить следующие задачи:

–определить количество и расположение корней;

–найти их приближенные значения (нулевые итерации) или определить отрезок, содержащий единственный корень.

Второй этап – уточнение приближенного значения корня до некоторой заданной точности ε.

2.1. Первый этап. Отделение корней

Отделить (локализовать) корни – это значит выделить из области допустимых значений функции y = f(x) отрезки, в каждом изкоторыхсодержитсяединственныйкорень.

Для функции общего вида не существует универсальных методов решения задачи локализации корней. Отделить корни уравнения f(x) = 0 можно разными способами. Рассмотрим некоторые из них.

1.Табулирование функции. Строится таблица значений функции у = f(x) на некотором отрезке x [a, b]. Если окажется, что для соседних значений аргумента значения функции имеют разные знаки, то хотя бы один корень уравнения (2.1) можетнаходитьсямежду ними.

2.Графический метод. Если удается построить график функции y = f(x), то можно определить количество и расположение нулей функции, выделяя те промежутки оси Х, где график y = f(x) пересекает ось Х.

Если построение графика y = f(x) затруднительно, то исходное уравнение f(x) = 0 заменяется эквивалентным

ему уравнением (x) = (x) и строятся графики функций

у1 = (x) и у2 = (x). Искомый корень является абсциссой точки пересечения графиков этих функций.

28

3.Определить корень исходя из физического смысла задачи.

4.Убедиться в том, что на данном отрезке x [a, b] (например, грубо определенном графическим способом) действительно имеется единственный корень уравнения (2.1), можно аналитическим способом, в основе которого лежит известная теорема математического анализа [3].

Теорема 2.1. Если непрерывная на отрезке [a, b] функция y = f(x) принимает на концах его противоположные знаки, т.е. f(a)f(b) < 0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x) = 0.

Корень заведомо будет единственным, если производная функции y = f'(x) существует и сохраняет постоянный знак внутри интервала (a, b), т.е. функция монотонна на отрезке [a, b].

Пример 2.1. Отделить (локализовать) корни урав-

нения

4 – ех – 2х2 = 0,

(2.2)

т.е. выяснить, сколько корней имеет это уравнение, и найти интервалы, в которых находятся по единственному корню.

Способ 1. Составим таблицу значений функции f(x) = 4 – ех – 2х2 на промежутке [–3, 1] (табулирование функции) (табл. 2.1).

	Таблица 2 . 1 .			Табулирование функции
x		–3		–2	–1	0		1
f(x) = 4 –	ех – 2х2	–14,049		–4,135	1,632	3,012		–0,718

Из таблицы видно, что на отрезках [–2,–1] и [0,1] существуетпо крайнеймере по одному корнюуравнения(2.2).

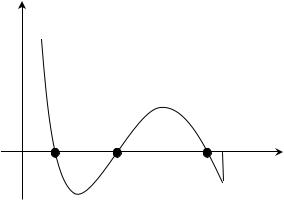
Способ 2. Уравнение (2.2) эквивалентно уравнению

(x) = (x), где (x) = 4 – 2х2; 3) (x) = ех.

29

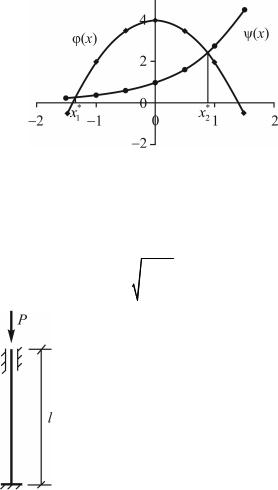
Построим графики функций у = (x) и у = (x) (рис. 2.2). Они пересекаются в двух точках, абсциссы кото-

рых х*1 и х*2 являются решениями уравнения (x) = (x), т.е. решением уравнения (2.2).

Рис. 2.2. Графический способ отделения корней
Пример 2.2. Локализовать корни уравнения
х – tg(x) = 0,	(2.3)

которое получается при решении задачи устойчивости

стержня (рис. 2.3), где

Рис. 2.3. К задаче устойчивости стержня

	x	Pкр	l .
		EJ

При решении задач устойчивости нас обычно интересует наименьшее значение критической нагрузки, т.е. надо найти наименьший положительный кореньуравнения(2.3).

Если при решении данной задачи отделение корней производить на основании таблицы табулирования (табл. 2.2), то можно допустить ошибку, предположив, что корень уравнения находится на отрезке [1, 5, 2], где функция меняет знак.

30