книги / Теория графов и её приложения.-1

А цикломатическое число:

λ(G) = A – S + 1 = 12 – 8 + 1 = 5.

Но позвольте, как же 5, когда у нас по каждой грани цикл?! А их 6.

Но то в пространстве трёхмерном…

Рис. 1.8. Развертка куба на плоскости в красках

Действительно, пять независимых циклов! А где шестой? Это – всё, что вне этих пяти! Куб – плоский граф!

Иначе изобразим куб – вот так – цикл, соответствующий нижней грани, содержит внутри себя 5 других циклов, поэтому его цикломатическое число и не учитывает (рис. 1.8).

Рис. 1.9. Развертка куба на плоскости вид сверху

21

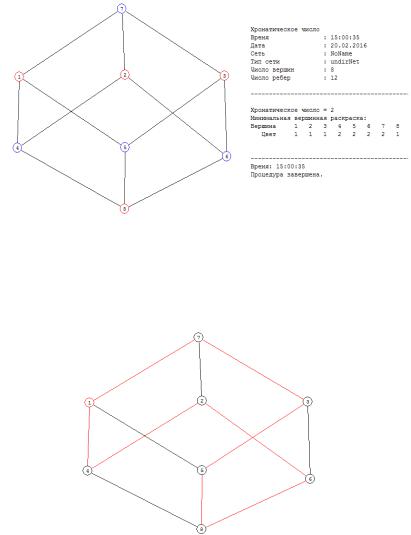
Это как пирамида майа.

Куб – бихроматический граф (рис. 1.10).

Рис. 1.10. Раскраска куба

Куб – гамильтонов граф (рис. 1.11).

Рис. 1.11. Гамильтонов цикл

22

ВыполняетсялиусловиеОре? ВыполняетсялиусловиеДирака? Существует ли эйлеров цикл?

Задания для «летучки». Изобразить ориентированный граф из четырёх вершин по заданному числу, полагая, что каждая цифра – строка матрицы смежности орграфа. Определить цикломатическое и хроматическое числа. Определить, является ли полученный граф эйлеровым и гамильтоновым? Получить матрицу всех путей в графе длиной 2 путем возведения в квадрат соответ-

ствующей булевой матрицы.
1)	4АD6;	2) 5BC4;	3)	794E;	4) 385С;	5) 2B18.
6)	19CC;	7) 72DD;	8)	5B16;	9) 6A5C;	10) 2258.

Будьте готовы к ответу на вопросы по занятию:

1.Что такое граф?

2.Каковы основные виды графов?

3.Что такое смежность, инцидентность.

4.Как задаются графы?

5.Как строятся матрицы смежности и инцидентности?

6.Что такое подграф и частичный граф?

7.Что такое цикломатическое число графа и как оно определяется?

8.Что такое хроматическое число графа?

9.Что такое степень вершины и чему равна сумма степеней вершин неориентированного графа?

10.Как получить матрицу всех путей длиной 2?

11.Поясните формулу Эйлера.

12.Как определяется наличие эйлерова цикла в графе?

13.Что такое гамильтонов граф?

14.Как формулируется условие Оре?

15.Как формулируется условие Дирака?

23

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2. ОПРЕДЕЛЕНИЕ ПРОСТЫХ МЕТРИК НЕОРИЕНТИРОВАННОГО ГРАФА

Вопросы занятия

1.Опрос по теоретическому материалу «Простые метрики неориентированного графа».

2.Коллективное решение задач по теме занятия у доски «вручную».

3.Самостоятельная работа по вариантам – на ПЭВМ в программе GRIN.

4.«Летучка».

Пример определения простых метрик неориентированного графа

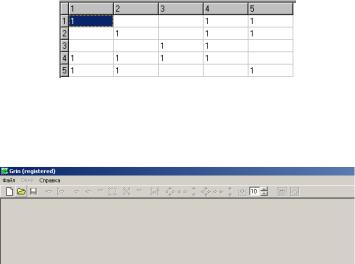
Дано: матрица смежности неориентированного графа (по вариантам) (рис. 2.1).

Рис. 2.1. Матрица смежности некоторого графа

По заданной матрице строим граф в свободно распростра-

няемой системе GRaph INterface (GRIN) (рис. 2.2).

Рис. 2.2. Экранная форма программы GRaph INterface (GRIN)

24

Создаём файл (рис. 2.3).

Рис. 2.3. Создание файла в программе GRIN

Создаём граф (рис. 2.4).

Рис. 2.4. Создание графа по матрице смежности (рис. 2.1)

Задаём: свойства – граф – простые метрики. Получаем результат (рис. 2.5).

25

Рис. 2.5. Результат определения простых метрик графа на рис. 2.4

Определяем плотность (рис. 2.6).

Рис. 2.6. Результат определения плотности графа рис. 2.4

Результат определения не плотности графа на рис. 2.4 представлен на рис. 2.7.

Рис. 2.7. Результат определения плотности графа на рис. 2.4

Наименьшее число вершин, покрывающих все рёбра, – вершинное покрытие (рис. 2.8).

26

Рис. 2.8. Результат определения вершинного покрытия графа на рис. 2.4

Вершинное покрытие – это число α0 = 2.

Наименьшее число рёбер, покрывающих все вершины, – рёберное покрытие α1, но оно почему-то не определяется в GRIN…

Определениехроматическогочислапредставленонарис. 2.9.

Цикломатическое число определяем вручную: Вершин 5, рёбер 5 Цикломатическое число равно 5 – 5 + 1 = 1

Действительно имеется всего один цикл 1,4,2,5 (рис. 2.10).

Рис. 2.9. Результат определения хроматического числа графа, представленного на рис. 2.4

27

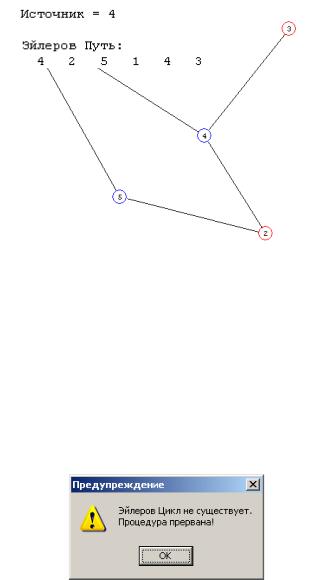
Рис. 2.10. Цикл 1,4,2,5 в графе, представленном на рис. 2.4

Определение эйлерова пути (рис. 2.11).

Рис. 2.11. Результат определения эйлерова пути графа на рис. 2.10

Определение эйлерова цикла, его нет (рис. 2.12).

Рис. 2.12. Результат определения эйлерова цикла графа на рис. 2.10

28

Определение гамильтонова пути для источника 3 (рис. 2.13).

Рис. 2.13. Результат определения гамильтонова пути графа, представленного на рис. 2.10

Определение гамильтонова цикла, его тоже, как и эйлерова,

нет (рис. 2.14).

Рис. 2.14. Результат определения Гамильтонова цикла графа на рис. 2.10

Определяем точки сочленения (рис. 2.15).

Рис. 2.15. Результат определения точек сочленения графа на рис. 2.10

Мост один (рис. 2.16).

29

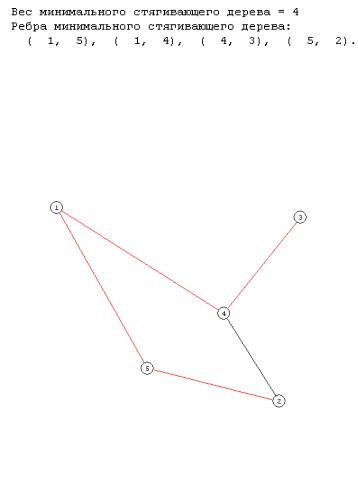
Рис. 2.16. Результат определения мостов графа на рис. 2.10

Группы автоморфизмов рассматриваются на отдельном занятии.

Теперь рассматриваем заданный граф, как сеть

Минимальное стягивающее дерево (представлено на рис. 2.17).

Рис. 2.17. Результат определения минимального стягивающего дерева графа на рис. 2.10

Пример определения покрытий орграфа. Пусть задан не-

который орграф (рис. 2.18).

Определение покрытий. Создадим граф в программе

GRIN (рис. 2.19).

30