8203

	f x .
2. f x dx		(1)

3.F x dx F x C , где C – произвольная постоянная.

4.

a f x dx a f x dx ,

a R,

a 0.

5.

f x g x dx f x dx g x dx .

2

Пример. Найти 3x

x dx .

x

Решение.

2

2

x

x

3x

x dx

3xdx

dx

xdx

1

1

1

1

x1 1

x 2

x

1 1

1

3 x1dx 2

dx

x 2 dx 3

2 ln

x

C

1

2

32 x2 2 ln x 23 x 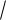x C.

4.Простейшие способы интегрирования.

Непосредственное интегрирование

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл удается привести к одному или нескольким табличным интегралам. К табличному виду обычно удается привести не очень сложные интегралы путем элементарных тождественных преобразований подынтегральных функций, а также воспользовавшись основными свойствами неопределенного интеграла. Поясним сказанное примерами.

Пример. Найти x 3 2 dx .

Решение.

40

x 3 2 dx x2 6x 9 dx x2dx 6xdx 9dx

	x3	6 xdx 9 dx		x3		6	x2	9x C		x3	3x2 9x C.
3			3			2			3
Выполнив под			знаком интеграла			очевидные			тождественные преобразования

(возвести разность в квадрат), свели данный интеграл к трем табличным интегралам xn dx, n 2;1; 0. постоянная C (которая в данном примере равна сумме трех постоянных C C1 C2 C3 ) появляется тогда, когда исчезают знаки интеграла.

Пример. Найти x2 1 dx . x

Решение.

x2 1

x2

1

x

1

dx

1

dx

dx

xdx

dx

x

x

x

x

x

x

2

ln

x

C .

2

Интегрирование заменой переменной.

Во многих случаях

f x dx можно упростить,

если вместо

x ввести

новую переменную t , положив

x t ,

(2)

тогда

dx

t dt .

Для приведения данного интеграла к новой переменной достаточно

привести к новой переменной его подынтегральное выражение

f x dx f t t dt ,

(3)

где

x t ,

41

e2 x 3dx .

в справедливости чего легко убедиться, продифференцировав обе части равенства (3) и воспользовавшись затем формулами (1) и (2).

Метод замены переменной интегрирования, является одним из наиболее эффективных и распространенных методов интегрирования. С другой стороны,

не существует общих правил, которые во всех случаях позволяли бы найти замену переменной, ведущую к желаемой цели. Поэтому, чем больше примеров самостоятельно решить, тем с большим успехом можно овладеть методом замены переменной.

Пример. Найти

	Решение.	Данный	интеграл не табличный, но					есть интеграл ex dx ,
	сходный с данным. Поэтому введем новую переменную t ,								связанную с x
	зависимостью:	2x 3 t ,		x	1	t 3 .	Дифференцируя			это	равенство,
				2
									1
	получим: 2x 3 dx		t dt ,	2dx dt ,			откуда	dx		dt .	Подставив
									2

результат в данный интеграл, имеем:

e2 x 3dx et 12 dt 12 et dt 12 et C.

Возвращаясь к переменной x , находим:

e2 x 3dx 12 e2 x 3 C .

Для надежности проверяем результат дифференцированием:

1

1

1

2 x 3

2 x 3

2 x 3

2 x 3

e

C

e

2x 3

e

2 e

– верно.

2

2

2

Интегрирование по частям.

42

Пусть u и v – две любые дифференцируемые функции от x , то есть

u u x и v v x . Тогда дифференциал произведения	u v вычисляется по
следующей формуле:
d uv udv vdu.
Отсюда, интегрируя обе части последнего равенства, находим:
d uv udv vdu ,
или
u v udv vdu ,
откуда
udv u v vdu .	(4)
Полученная формула называется формулой интегрирования по частям для
неопределенного интеграла. Она сводит нахождение	интеграла udv к

нахождению интеграла vdu , и если функции u и v удается подобрать так,

чтобы последний интеграл брался проще, чем исходный, то цель будет достигнута.

Пример. Найти xex dx.

Решение.		Пусть	u x ,	x		dx , тогда
				dv e				du x dx 1 dx dx,
v ex dx ex . По формуле (4) находим:
		xex dx xex ex dx xex ex C ,
			xex dx x 1 ex C .
Пример. Найти x2 ln xdx.
Решение.		Пусть	u ln x ,			2	dx,
					dv x			тогда du ln x dx ,
v x2dx	x3	. По формуле (4) находим:
3

43

x2 ln xdx	x3	ln x		x3			1	dx	x3	ln x			1			x2dx		x3	ln x	1			x3	C ,
3				3			x	3				3				3				3		3
				2							1					x3
		x			ln xdx ln x												C .
											3					3

§ 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Важным средством исследования в математике, физике, механике и

других дисциплинах является определенный интеграл – одно из основных

понятий математического анализа.

1.Задачи, приводящие к понятию определенного интеграла

Кпонятию определенного интеграла приводят задачи вычисления площадей плоских фигур, длин дуг, объемов тел, вычисление работы, массы неоднородных стержней, центров тяжести плоских фигур и дуг и т.д.

Рассмотрим некоторые из них.

2. Площадь криволинейной трапеции

Криволинейной трапецией назовем плоскую геометрическую фигуру,

ограниченную двумя прямыми x a и x b a b , отрезком a,b оси OX

и графиком некоторой непрерывной функции y f x , x a,b f x 0 .

44

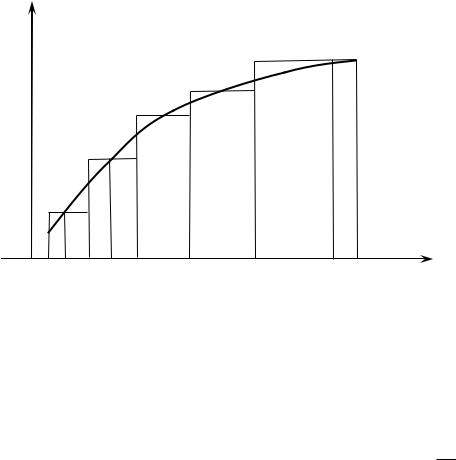
y

y f x

x0 a P1 x1 P2 x2 xn 1 Pn xn b x

Рис. 20

Найдем площадь S этой фигуры. Для этого:

1)разобьем отрезок a,b произвольно расположенными, но следующими друг за другом точками x0 a , x1 , x2 ,..., xn b ;

2)в каждом из полученных отрезков длины xi xi xi 1 i 1, n 1,2, , n

выберем произвольную точку Pi xi 1 Pi xi и вычислим значение функции в

i
этих точках f P		i 1, n ;
3) рассмотрим прямоугольники с основаниями									xi и высотами		f Pi
i 1, 2,..., n и	найдем их площади						f Pi xi	i	1, 2,..., n .	Сложив эти
				~		n	xi . Значение				~
числа, получим	сумму			S		f Pi			полученной	суммы S
						i 1
									n
приближенно равно площади S криволинейной трапеции S f Pi xi											(чем
									i 1
мельче отрезки xi		i 1, 2,..., n , тем лучше будет это приближение);

4) введем обозначение: max xi . Для получения точного выражения площади S криволинейной трапеции надо перейти к пределу в полученной

сумме ~ при и n , т.е.

S 0

45

n

S lim f Pi xi .

0 i 1 n

3. Масса линейного неоднородного стержня

Рассмотрим стержень постоянного сечения длины b a (отрезок a,b ).

Если стержень однородный, т.е. плотность в каждой точке x которого постоянна и равна , то масса стержня M вычисляется по формуле

M b a .

Пусть стержень неоднородный и в каждой точке

x известна плотность

f x . Найдем массу M этого неоднородного стержня. Для этого:

1)

разобьем

отрезок

a,b

на

n

отрезков

точками

a x0 x1

... xn b;

xi 1 i

выберем

2) в

каждом из полученных отрезков xi

xi

1, n

произвольную точку Pi

xi ,

i

в

i

1, n

и вычислим плотность f Pi

1, n

каждой точке Pi . Будем считать,

что на каждом отрезке xi

i 1, 2, , n

плотность постоянна и равна

f Pi . Тогда масса

участка xi

приближенно

равна f Pi

xi ;

n

3) составим сумму f Pi xi . Она приближенно равна массе M

i 1

неоднородного стержня;

4) для получения точного выражения массы M стержня перейдем к пределу при 0, max xi и n :

n

M lim f Pi xi .

0 i 1 n

4. Работа переменной силы на прямолинейном участке пути

46

Допустим, что некоторая сила f

f

x , направленная вдоль оси OX , на

отрезке a,b совершает работу (см. рис.

21). Если

f const,

то работа A

вычисляется по формуле A f b a .

Определим работу A переменной силы f x на отрезке a,b :

f x

a

x

x

b

Рис. 21

Для этого: разобьем отрезок a,b с помощью произвольно

расположенных, следующих друг за другом точек x0 a ,

x1 , x2 , ..., xn

b . Это

разбиение

производим достаточно

мелко,

так,

чтобы

на

интервалах

xi xi xi 1

i

величина

f x практически не изменялась. Пусть она

1, n

равняется

f Pi , Pi

xi , xi xi xi 1

i 1, 2, , n

( Pi

– произвольно

выбранные точки). Величина работы силы

f Pi

на участке xi

вычисляется по

формуле: Ai f Pi

xi .

Определение.

Предел

n -ой

интегральной

суммы

для

функции

y f x

на отрезке a,b при

0

max xi

и n называется

определенным

интегралом от функции

y f x

в пределах

от

a до b

b

(обозначение

f x dx ), т.е.:

a

lim

n

f P x

b f x dx ,

0

i

i

n

i 1

a

где a – нижний предел интегрирования, b – верхний предел интегрирования,

47

f x dx

– подынтегральное выражение, f x – подынтегральная функция.

Одним из геометрических смыслов определенного интеграла является то, что определенный интеграл равен площади криволинейной трапеции.

Физический смысл определенного интеграла. Здесь его возможности очень широки. В частности, можно определить массу стержня, работу силы на заданном отрезке пути и т.д.

5. Свойства определенного интеграла

Свойства определенного интеграла вытекают из основных свойств сумм и пределов:

1. Постоянный сомножитель можно вынести за знак определенного интеграла:

b	b
k	f x dx k	f x dx ,	k const.
a	a

2.Определенный интеграл от алгебраической суммы двух функций

f1 x и	f2 x , интегрируемых на	a,b ,	равен алгебраической сумме
определенных интегралов от этих функций, т.е.
	b	b	b
	f1 x f2 x dx f1 x dx f2			x dx .
	a	a	a

Данное свойство распространяется и на сумму любого конечного числа интегрируемых функций.

3.Если отрезок интегрирования a,b разбит точкой c на два отрезка

a, c и c,b , то интеграл по всему отрезку равен сумме интегралов по его

частям:

48

b	c	b
f x dx f x dx f x dx .
a	a	c

Точка c может находиться и вне отрезка a,b .

4. Интеграл с равными пределами интегрирования a b равен нулю,

т.е.

a

f x dx 0 .

a

5. Если в определенном интеграле поменять местами пределы интегрирования, то знак интеграла изменится на противоположный:

b	a
f x dx f x dx .
a	b

6.Теорема о среднем значении:

Если y f x непрерывна на a,b , то существует такая точка c a, b ,

что справедливо следующее равенство:

b

f x dx f c b a .

a

Нетрудно понять геометрический смысл этого равенства: интеграл,

стоящий слева есть площадь криволинейной трапеции. Произведение, стоящее в правой части равенства, - площадь равновеликого ей прямоугольника с высотой f c и основанием b a (см. рис. 22).

49