8393

Таким образом, сумма нормальных напряжений на двух взаимно перпендикулярных площадках есть величина постоянная и от положения этих площадок не зависит.

Следовательно, если по одной из таких площадок нормальные напряжения имеют максимальное значение, то по другой они имеют минимальное значение.

При расчете инженерных конструкций нет необходимости определять нормальные напряжения по всем площадкам, проходящим через заданную точку. Достаточно знать максимальные и минимальные их значения, которые, как отмечалось ранее, называются

главными напряжениями.

Для определения величин главных напряжений и положения главных площадок функцию для σα (3.3) исследуем на экстремум, т.е. приравняем нулю первую производную от напряжения σα по α при некотором значении угла α = α0:

dσαα = -σx × 2sin α× cos α + σy × 2sin α× cos α - τyx 2cos 2α. d

При a = a0 , используя известные тригонометрические зависимости, получим:

dσ		α		= -2 × (	σx	− σy	× sin2α		+ τyx cos2α0 ) = 0 .
								0		(3.6)′
	dα					2
			α=α0
					1444442444443

τα0

Здесь α0 – угол наклона главной площадки к площадке, в которой действуют заданные напряжения σх (рис. 3.3б).

Сравнивая выражение (3.6)′ с формулой (3.4), устанавливаем, что

	dσ		α		= -2 × τα = 0 .
		dα
				α=α0	0

Отсюда следует, что на главных площадках касательные напряжения равны нулю, т.е.:

τ α 0 =	σ х	- σ у	×sin2α		+ τ yx cos2α0	= 0 .	(3.7)
				0
		2

Из соотношения (3.7) получим:

		tg2α0	= -		2τyx				,	(3.8)
					σx	- σy
	или, используя (3.2):
			0 =		2τxy
		tg2α					.			(3.9)
				σx		- σy

Формулы (3.8) и (3.9) дают значения углов α0, определяющие две взаимно перпендикулярные площадки, на которых действуют главные напряжения.

Следовательно, для определения положения главных площадок, необходимо площадки, на которых действуют заданные напряжения σx и σy, повернуть на угол α0 против хода часовой стрелки (при α0 > 0) или по ходу часовой стрелки (при α0 < 0).

Следует иметь в виду, что наибольшее главное напряжение должно проходить в тех четвертях, где сходятся касательные напряжения tуx и tху , и оно всегда находится ближе к тому из заданных нормальных напряжений, значения которого с алгебраической точки зрения больше.

Главные напряжения можно определить, подставляя значения угла α0 в формулу (3.3).

Эти же напряжения можно определять и без предварительного определения угла α0, если (3.8) или (3.9) подставить в формулу (3.3). В результате элементарных преобразований получаем следующую формулу для определения величин главных напряжений:

σx + σy

1

σ

max

= σ

=

±

× (σ

x

- σ

y

)2 + 4τ2 .

(3.10)

1,2(3)

2

2

yx

min

Определим также площадки, по которым касательные напряжения имеют экстремальные (максимальные и минимальные) значения. Такие площадки называются

площадками сдвига.

Для этого приравняем нулю первую производную функции (3.4) при некотором значении угла α1:

	dτ		α				= (σx - σy )cos2α1		- 2τyx sin2α1 = 0 .
	dα α=α
				1
Отсюда:	tg2α1			=		σx	− σy	.	(3.11)
						2τyx

Здесь α1 – угол наклона площадки сдвига к заданной площадке, по которой действует напряжение σх. Если угол α1 положителен, то эту площадку надо повернуть против хода часовой стрелки, а если отрицателен – то по ходу часовой стрелки.

Формула (3.11) дает значение угла α1, определяющее положение одной из двух взаимно перпендикулярных площадок. Положение другой площадки определяется поворотом на угол α+900. По одной из двух площадок действует максимальное касательное напряжение τmax, а по другой – минимальное τmin. Из закона парности касательных напряжений следует, что

τmax = -τmin .

Если определены главные площадки, легко определить величины напряжений τmax и

min

положение площадок, на которых они действуют.

Если в формуле (3.4) для определения касательных напряжений τα на произвольной площадке за исходные примем главные напряжения σ1 и σ3 вместо σx и σy, а τуx = 0, то получим:

	τα = σ1 − σ3 ×sin2α.						(3.12)
	2
Отсюда следует, что		τmax	= ±	(σ1 − σ3 )		,	(3.13)
		min	2

так как sin(2 α ) = ±1 при α = ±450 , т.е. площадки сдвига наклонены к главным площадкам

под углом ±45˚.

Если в формулу (3.13) подставим выражения σ1 и σ3 из соотношения (3.10), найдем:

			1
	τmax	= ±			(σx - σy )2 + 4τ2уx		.	(3.14)
	min	2

Определим нормальные напряжения на площадках сдвига. Для их определения формулу (3.3) перепишем, подставляя вместо напряжений на произвольных площадках sх и sу главные напряжения s1 и s3, а tух = 0:

σ	α	= σ cos2	α + σ	sin2α .	(3.15)
		1	3

При α = ±45˚ получим формулу для определения нормальных напряжений на площадках сдвига:

		= σ		1 2			+ σ		1		2	=	σ + σ
σ	α=±45°							3					1	3 .	(3.16)
		1							2				2
					2

Таким образом, из (3.15) следует, что нормальные напряжения на двух взаимно перпендикулярных площадках сдвига равны между собой по величине и знаку.

Если нормальные напряжения на площадках сдвига равны нулю, то такие площадки называются площадками чистого сдвига.

Примерами чистого сдвига являются кручение и срез.

3.3. Исследование объемного напряженного состояния

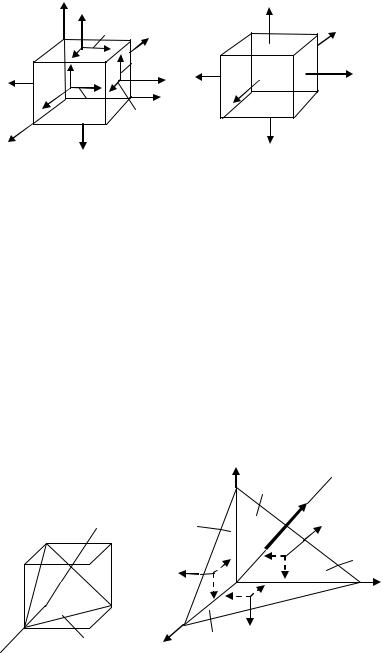
Как было показано ранее в п. 3.1, напряжения, действующие на гранях элементарного параллелепипеда, в общем случае напряженного состояния представляются в виде тензора напряжений (рис. 3.1а), как упоминалось:

			σx		τxy		τxz
T	=	τ		yx	σ	y	τ		.
σ								yz
			τzx		τzy		σz

Тензор напряжений симметричен относительно главной диагонали, поскольку по закону парности касательных напряжений имеем:

τxy = τyx , τxz = τzx , τyz = τzy .

Рассмотрим определение главных напряжений и положения главных площадок в случае объемного напряженного состояния (все три главных напряжения не равны нулю) (рис. 3.1б).

	Y					б)	σ 2
а)		sy						σ 3
			tXY	σ z
	tZY
				tYX σ х
σ х		tYZ				σ 1		σ 1
	σ z	tXZ			Х		σ 3
				tZX
								s1	¹ 0
Z		σ у					σ 2	s2	¹ 0
							s1 ³ s2 ³ s3	s3 ¹ 0
					Рис. 3.4

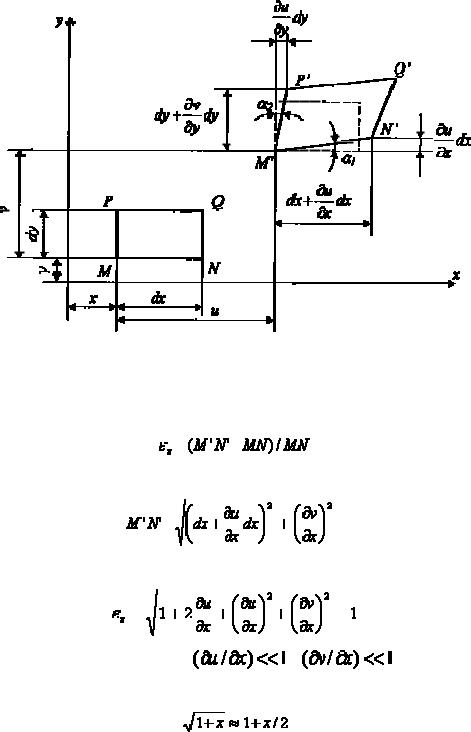
Предположим, что нам известно положение главной площадки, определяемой нормалью ν . Сечением, параллельным этой площадке, выделим из исходного параллелепипеда тетраэдр, изображенный на рис. 3.4б, и составим условия равновесия тетраэдра в виде суммы проекций действующих на него сил на оси координат. Введем обозначения для направляющих косинусов нормали ν :

cos(x,ν) = L ; cos(y,ν) = m; cos(z,ν) = n.

(3.17)

Примем площадь наклонной грани тетраэдра dA = 1, тогда площади других граней будут: dAX = L , dAy = m, dAZ = n.

а)					б)	У			ν
								dA=1
У									σгл	= σ
				dAx= L
		ν							σz
						τxz
				σx				τzx	τzy	dAz = n
					τzy			τyz
						τ				Х
							yx
			Х					σ y
					dAy=m
	Главная			Z
	площадка

Z

Рис. 3.5

Единственное напряжение, действующее на главной площадке, обозначим σгл = σ . Сумма проекций сил на ось Х запишется в виде:

σL − σхL − τух m − τzx n = 0.

Аналогичные равенства будут для осей Y и Z. Все вместе они составят систему однородных уравнений относительно неизвестных косинусов L , m и n:

(σx − σ)L + τyx m + τzx n = 0

τxyL + (σy − σ)m + τzy n = 0 . (3.18) τxz L + τyz m + (σz − σ)n = 0

Так как между неизвестными существует зависимость

L2 +m2+n2 = 1,

(3.19)

то одновременно они все не могут быть равны нулю. В этом случае (доказано в линейной алгебре) определитель однородной системы уравнений равен нулю, т.е.

(σx − σ)	τyx	τzx
τxy	(σy − σ)	τzy	= 0.	(3.20)
τxz	τyz	(σz − σ)

Раскрыв определитель, получим кубическое уравнение

σ3 − I σ2	+ I	σ − I	3	= 0,	(3.21)
1	2

три корня которого и будут значениями трех главных напряжений в рассматриваемой точке.

Коэффициенты уравнения (4.20) получаются при раскрытии определителя (4.19) и имеют следующий вид:

I1 = σx + σy + σz ;

I

= σ

σ

y

+ σ

σ

z

+ σ

σ

z

− τ2

− τ2

− τ2 ;

(3.22)

2

x

x

y

yx

zx

zy

I = σ

σ

σ

z

− σ

τ2

− σ

τ2

− σ

τ2

+ 2τ

yx

τ

zx

τ

zy

.

3

x

y

x

zy

y

zx

z

yx

Эти коэффициенты не зависят от выбора осей координат, поскольку при любых исходных площадках уравнение (3.21) должно давать одни и те же корни σ1 , σ2 иσ3 –

главные напряжения в точке. Они называются первым, вторым и третьим инвариантами напряженного состояния (тензора напряжений).

Для определения направляющих косинусов L, m, n, соответствующих одной из трех главных площадок, значение главного напряжения на этой площадке надо подставить

в (3.18) вместо σ . Совместное решение уравнений (3.18) и (3.19) и даст искомые значения направляющих косинусов L, m, n.

3.4 Тензор деформаций

Рассмотрим вначале случай плоской деформации (рис. 3.6). Пусть плоский элемент MNPQ перемещается в пределах плоскости и деформируется (изменяет форму и размеры). Координаты точек элемента до и после деформации отмечены на рисунке.

Рис.3.6. Плоская деформация.

По определению относительная линейная деформация в точке М в направлении оси Ох равна

.

Из рис. 3.6 следует

.

Учитывая, что MN=dx, получим

.

В случае малых деформаций, когда

,

, можно пренебречь

квадратичными слагаемыми. С учетом приближенного соотношения

справедливого при x<<1, окончательно для малой деформации получим

.

. В случае малых

Угловая деформация

определяется как сумма углов

и

деформаций

Для угловой деформации имеем

Проводя аналогичные выкладки в общем случае трехмерной деформации,

имеем девять соотношений связывающих линейные и угловые деформации с

перемещениями. Эти соотношения носят название соотношений Коши:

(3.23)

Три линейных и шесть угловых деформаций (3.23) образуют тензор малых деформаций

(3.24)

Этот тензор полностью определяет деформированное состояние твердого тела. Он обладает теми же свойствами, что и тензор напряжений. Свойство симметрии непосредственно следует из определения угловых деформаций. Главные значения и главные направления, а также экстремальные значения угловых деформаций и соответствующие им направления находятся теми же методами, что и для тензора напряжений.

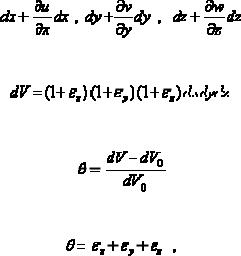
Инварианты тензора деформаций определяются аналогичными формулами, причем первый инвариант тензора малых деформаций имеет ясный физический смысл. До деформации его объем равен dV0=dxdydz. Если пренебречь деформациями сдвига, которые изменяют форму, а не объем, то после деформации ребра будут иметь размеры

(рис. 3.6), а его объем будет равен

.

Относительное изменение объема

в пределах малых деформаций составит

что совпадает с определением первого инварианта. Очевидно, что изменение объема есть физическая величина, не зависящая от выбора системы координат.

Так же, как и тензор напряжений, тензор деформаций можно разложить на шаровой тензор и девиатор. При этом первый инвариант девиатора равен нулю,

т. е. девиатор характеризует деформацию тела без изменения его объема.

3.5 Обобщенный закон Гука

Установим зависимость относительной линейной деформации от нормальных напряжений в случае объемного напряженного состояния.

Определим относительную продольную деформацию выделенного элемента (см. рис. 2.1б) в направлении главного напряжения σ1, отдельно рассматривая влияние

каждого из главных напряжений и складывая результаты в соответствии с принципом независимости действия сил:

ε1 = ε11 + ε12 + ε13 .

(3.25)

Под действием напряжения σ1 элемент в направлении этого напряжения на основании закона Гука получит относительное удлинение, равное ε11 = σЕ1 . Аналогично определятся относительные деформации по направлениям двух других главных напряжений:

ε22 = σЕ2 ; ε33 = σЕ3 .

Вто же время по отношению к напряжениям σ2 и σ3, ребро элемента, параллельное σ1, является поперечным размером, а потому под действием напряжений σ2 и σ3 элемент в направлении σ1 испытывает относительные укорочения, равные:

ε	= -ν×ε	22	= -ν	σ2 , ε = -ν×ε		33	= -ν σ3 .	(3.26)
12				Е	13		Е

Здесь ν = εε' – коэффициент поперечной деформации, называемый коэффициентом

Пуассона; ε' – относительная поперечная деформация; ε – относительная продольная деформация.

Таким образом, полная относительная деформация элемента в направлении напряжения σ1 выразится суммой:

ε1 = ε11 + ε12

+ ε13

=

σ1

- ν

σ2

- ν

σ3

=

1

[σ1 - ν(σ2 + σ3 )] .

(3.27)

Е

Е

Е

Е

Подобные же выражения получим и для деформаций в двух других направлениях. В результате имеем:

ε =			1		[σ − ν(σ					+ σ		)]
									2		3
	1			Е	1
			1
ε2		=				[σ2		− ν(σ1		+ σ3 )] .				(3.28)
				Е
ε		=		1		[σ		− ν(σ + σ				)]
	3						3				2
				Е					1

Касательные напряжения не вызывают удлинений ребер выделенного параллелепипеда, а вызывают лишь изменения прямых углов между его гранями. Закон Гука в общем виде (рис. 2.1а) для объемного напряженного состояния запишется:

εx

εy

εz

				1
	=				[σx − ν(σy + σz )]
				Е
				1
	=				[σy − ν(σx	+ σz )] ,
				Е
				1
	=				[σz − ν(σx	+ σy )]
				Е

			τxу				2(1 + ν)
γxу	=				=				τxу
			G				E
			τ	уz		2(1 + ν)
γуz	=				=				τуz .	(3.29)
			G
							E
			τ				2(1 + ν)
γzx	=			zx	=				τzx
			G				E

В соотношениях (3.29) использована зависимость между тремя упругими постоянными материала – модулем упругости 1-го рода Е, коэффициентом Пуассона ν и модулем упругости 2-го рода (модулем сдвига) G:

	Е
G =	2(1 + ν) .	(3.30)

Формулы (3.29) показывают, что при изменении нормальных и касательных напряжений на всевозможных площадках, проходящих через заданную точку, соответственно изменяются относительные линейные деформации и углы сдвига граней выделенного элемента с бесконечно малыми размерами dx, dy, dz.

Совокупность линейных относительных деформаций и углов сдвига для всевозможных направлений осей, проведенных через заданную точку, называется деформированным состоянием в точке.

Деформации элемента в трех ортогональных плоскостях представим в виде таблицы

				1			1
	εx					γyx			γzx
				2			2
1							1
			γxy	εy					γzy	(3.31)
	2						2
	1			1
	2		γxz	2		γyz	εz

аналогичной тензору напряжений и называемой тензором деформаций.

Выражения (3.29) , устанавливающие связь между деформациями и напряжениями в общем случае напряженного состояния, носят название обобщенного закона Гука. Они применимы при напряжениях, не превышающих предел пропорциональности материала и при малых деформациях.

С помощью формул (3.29) обобщенного закона Гука можно определять относительные деформации по любому заданному направлению, если предварительно определить