10309

нуля). Эти свойства используются для раскрытия неопределенностей при нахождении предела функции аналогично тому, как это делалось при нахождении пределов последовательностей.

17.2. Первый замечательный предел. Продемонстрируем в каче-

стве примера нахождение так называемого первого замечательного пре-

дела

		lim	sin x	1.		(17.1)
		x 0	x
	В данном случае мы имеем неопределенность вида				0	. Поскольку функ-
					0
	ция f (x) sin x	– чётная и нас интересует её поведение при					x 0, то
	x

значение аргумента x , измеряемое в радианах, будем считать положительным и малым. Рассмотрим часть дуги окружности AFC единичного радиуса.

Рис. 17.2

Площадь сегмента AFC меньше площади прямоугольника ABCD , поэтому для них имеем неравенство:

0 SAFC SABCD .					(17.2)
Площадь сегмента найдём как разность площадей сектора					OAFC и тре-
угольника OAC
SAFC	1	x	1	sin x 0 .
			2
2

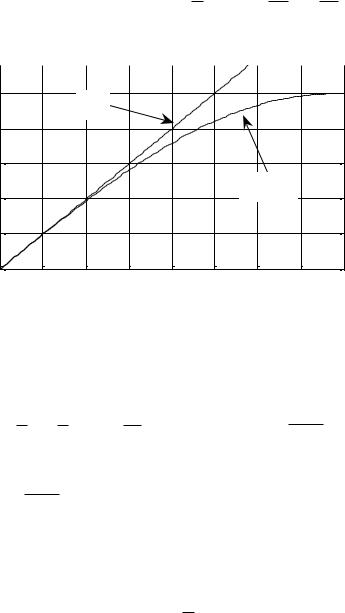
Отсюда следует неравенство sin x x ( x 0 ). Полезно представить его графическую иллюстрацию (см. рис. 17.3). Применим это неравенство для оценки площади прямоугольника ABCD

120

SABCD sin x (1 cos x) 2sin					2	x	sin x	2	x2	x3
					2				x	2
									4
1		y=x
0.8
0.6
0.4							y=sinx
0.2
00	0.2	0.4	0.6	0.8			1	1.2	1.4	1.6
			Рис. 17.3
Тогда неравенство (17.2) примет вид
0	1 x	1 sin x x3		или			0 1 sin x x2 .
	2	2	2						x
Когда x 0 , то 1 sin x		0 ,	а это и означает (17.1).
	x
Второй замечательный предел, когда аргумент принимает веще-
ственные значения,	имеет вид
				1	1	x
			lim		x		e .
			x
17.3. Непрерывность функции. Понятие предела функции позволяет
сформулировать такое важное свойство функции как ее непрерывность в
данной точке. Интуитивно ясно, что непрерывной зависимости соответ-
ствует ситуация, когда «малое» изменение аргумента вызывает «малое» из-
менение значения функции. Геометрически это означает, что график этой
функции рисуется, не отрывая карандаша от бумаги, т.е. непрерывно. Мате-
матически это понятие определяется следующим образом.
Функция f (x) непрерывна в точке x0 , если эта точка вместе с неко-
торой ее окрестностью входит в область определения функции и

lim f (x) f (x0 ) .

(17.3)

x x0

121

Фактически условие (17.3) означает, что

lim f (x) f (lim x) ,
x x0	x x0

т.е. при нахождении предела непрерывной функции знак предела и знак функции можно менять местами. Пример использования этого свойства непрерывной функции рассмотрим в связи с отысканием следующего предела

				3n					n	6						n	6
		2				( 2)							( 2)
lim	1				lim 1			2			lim	1			2			e 6
						n					n		n
n		n			n

Здесь мы поменяли местами порядок взятия предела и вычисления функции и применили второй замечательный предел.

Условие (17.3) также может быть записано в эквивалентном виде

lim [ f (x) f (x0 )] 0 ,
x x0 0
означающее, что приращение непрерывной функции f	f (x) f (x0 )

стремится к нулю, когда приращение аргумента x x x0 стремится к нулю, т.е.

lim f 0 .

x 0

Из определения следует, что для непрерывной в точке функции предел слева равен пределу справа и равен значению функции в этой точке

lim	f (x)	lim f (x) f (x0 ) .	(17.4)
x x0 0		x x0 0

Если нарушается хотя бы одно из этих равенств и оба односторонних предела существуют и конечны, то говорят, что в данной точке функция имеет разрыв первого рода. В остальных случаях нарушения условий непрерывности, т.е. когда хотя бы один из односторонних пределов не существует или равен бесконечности, у функции в этой точке разрыв второго

рода. Например, функция y | xx | непрерывна во всех точках области опре-

деления, а в точке x0 0 «терпит» разрыв первого рода.

Отметим так называемый устранимый разрыв, когда односторонние пределы в точке конечны и равны, а в самой точке функция или не опреде-

122

лена или ее значение не совпадает с односторонними пределами. В этом слу-
чае можно или доопределить или изменить значение функции в этой точке
так, чтобы ее значение было равно односторонним пределам (17.4), тем са-
мым получив непрерывную функцию.				Например,		функция	y sin x не
							x
определена в точке	x0 0 .	Учитывая первый замечательный предел, до-
определим её до непрерывной функции следующим образом:
		sin x			, x 0
		y	x
			1,		x 0
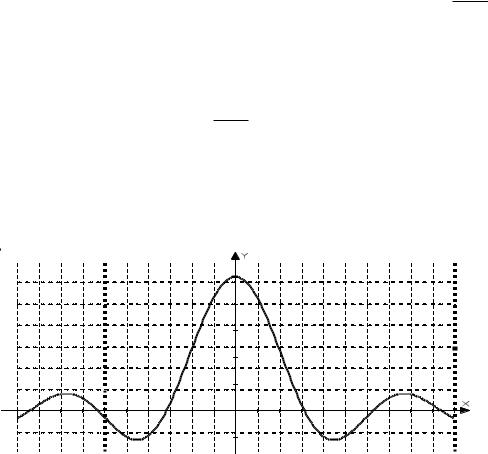
Это непрерывная в точке x0 0 функция (см. рис. 17.4).
			1
		0.75
		0.5
		0.25
-9	-6	-3	0		3	6	9
		-0.25
		Рис. 17.4
17.4. Свойства непрерывных функций. Функция называется непре-
рывной в данном интервале, если она непрерывна во всех точках этого
интервала. Все элементарные функции непрерывны в областях их опреде-
ления. Соответствующие свойства предела функции позволяют утвер-
ждать, что сумма, произведение, частное (когда знаменатель не равен
нулю) непрерывных функций есть непрерывная функция.
Покажем, что сложная функция, представляющая собой суперпози-
цию непрерывных функций, является					непрерывной. Пусть		y f (u) и
u (x) – непрерывные функции своих аргументов. Тогда

lim f ( (x)) f (lim (x)) f ( (x0 )) ,
x x0	x x0

т.е. сложная функция f ( (x)) – непрерывна.

Очевидно также, что обратная к непрерывной функции тоже непрерывна (напомним, что графики взаимно обратных функций симметричны относительно биссектрисы первого координатного угла).

123

Если непрерывная функция на концах замкнутого промежутка принимает значения разных знаков, то внутри этого промежутка найдется, по крайней мере, одна точка, в которой функция обращается в ноль (см. рис.17.5).

Рис. 17.5

Это свойство применяется для поиска решения уравнения f (x) 0 в

заданном промежутке. Обычно задают допустимую погрешность , с которой этот корень нужно вычислить. Это значит, что нужно найти такой промежуток [a,b] , содержащий корень ( f ( ) 0 ), что его длина b a .

Предполагается, что вычисление значений функции f (x) проблемы не составляет. Рассмотрим метод поиска корня на примере уравнения

f (x) x3 3x2 3 0 .

Функция f (x) всюду непрерывна. То, что это уравнение имеет, по

крайней мере, один корень, видно из следующего представления этой функции

f (x) x3 (1 3x x32 ) .

При больших по абсолютной величине значениях x знак функции f (x) определяется первым из множителей. Поэтому при x , f (x) 0 , а при x , f (x) 0 . Значит, график непрерывной функции, по крайней мере, один раз пересечёт ось абсцисс. Сделаем попытку графического решения уравнения, представив его следующим образом: x3 3(x2 1) .

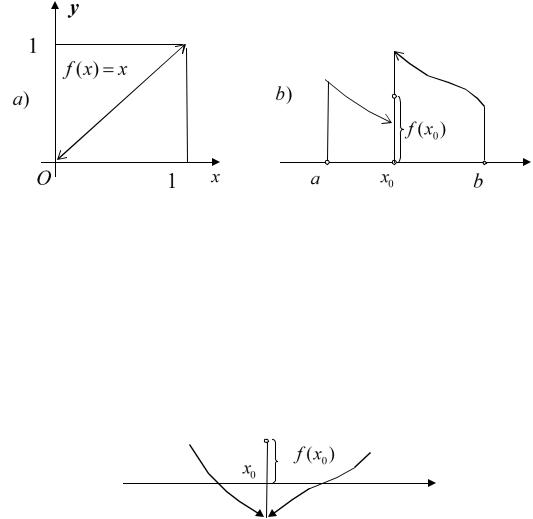
Видно, что в пределах чертежа обнаружились два корня, являющиеся абсциссами точек пересечения графиков функций y 3(x2 1) и y x3 (см.

рис.17.6). Так как y x3 при x 0 растет быстрее, чем y 3(x2 1) , то гра-

124

фики этих функций пересекутся еще раз. Действительно, вычислив значе-
ния	f (2) 1 0		и	f (3) 3 0 , убеждаемся, что этот корень находится
в промежутке		2 x 3 .
		5
		4			y=3 (x2 -1 )
		3
		2
		1			-1<x<0.5
		0
		-1
								1<x<1.5
		-2
					y=x3
		-3
		-4
		-1.5		-1	-0.5	0	0.5	1	1.5	2

Рис. 17.6

Вычислим с точностью до 0,1 корень уравнения из промежутка [1;1,5]. Воспользуемся так называемым методом деления пополам. Подсчитаем значения функции в «средней» точке этого промежутка f (1,3) 0,127 0 и на одном из его концов f (1,5) 0,375 0 . Следовательно, корень находится в промежутке 1,3 x 1,5. Снова находя значение функции в средней точке f (1,4) 0,136 0 , убеждаемся, что корень находится в промежутке 1,3 x 1,4 . Таким образом, поставленная задача решена. В дальнейшем мы познакомимся с более совершенными методами вычисления корней, где для достижения цели не требуется столь частого вычисления значений функции.

Рис. 17.7

125

Непрерывная функция ограничена на замкнутом промежутке и принимает свои наименьшее и наибольшее значения в этом проме-

жутке m f (x1 ) f (x) f (x2 ) M .

Если функция определена на открытом промежутке, то она может быть неограниченной в этом промежутке. Например, функция f (x) 1/ x не

ограничена в промежутке (0,1) . В открытом промежутке функция, будучи

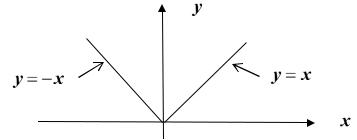
даже ограниченной, может не иметь ни наименьшего, ни наибольшего значений. Например, функция f (x) x в промежутке (0,1) (см. рис. 17.8 a ).

Если промежуток замкнут, но функция имеет разрыв в некоторой точке x0 , то функция может быть как неограниченной (в случае разрыва второго

рода), так и может не иметь ни наименьшего, ни наибольшего значений в заданном замкнутом промежутке (см. рис. 17.8 b ).

Рис. 17.8

Если непрерывная функция положительна (отрицательна) в некоторой точке, то существует окрестность этой точки, в которой функция сохраняет знак.

На рис. 17.7 в точке x1 функция отрицательна и существует некоторая

окрестность этой точки, в которой знак функции сохраняется. Для разрывной функции, как это видно из следующего рисунка, это не так.

Рис. 17.9

126

Значение функции в точке x0 положительно, но в любой малой окрестности этой точки функция принимает только отрицательные значения.

Лекция 18. Производная

18.1. Физический, геометрический и математический смысл произ-

водной. Одним из основных понятий математического анализа является понятие производной функции. Прежде чем привести его математическое определение, рассмотрим несколько задач, приводящих к этому понятию.

Первая задача связана с определением мгновенной скорости движущейся точки. Пусть известен закон движения точки x(t) , движущейся по

прямой O x . Если точка движется равномерно, т.е. за равные промежутки времени она проходит одинаковые расстояния, то ее скорость равна

	v(t)	x(t) x(0)	const .
		t

Если точка движется неравномерно, то что мы будем понимать под скоростью точки?

За промежуток времени [t,t t] точка проходит расстояниеx x(t t) x(t) . Если величина t достаточно мала, то можно считать,

что в этом промежутке точка движется равномерно и тогда приближенно ее скорость равна

v(t) xt .

Величина v(t) тем ближе к скорости в момент времени t , чем меньше

t . Скоростью точки в момент времени t назовем предел этого отношения, когда длина интервала времени t стремится к нулю, т.е.

v(t) lim x(t t) x(t) .

t 0 t

Вторая задача связана с понятием плотности массы тонкого неоднородного стержня. Пусть поперечное сечение стержня мало по сравнению с его длиной. Тогда плотность массы (x) этого стержня в точке с координа-

той x определим как предел отношения массы m m(x x) m(x) части стержня [x, x x] к ее длине x , т.е.

x lim	m x x m x	.
x 0	x
	127

Третья задача связана с проведением касательной прямой к заданной кривой.

Рис. 18.1

Под касательной к графику функции y f (x) в точке M 0 будем понимать предельное положение секущей M 0 M , когда точка M движется вдоль кривой к точке M 0 или, другими словами, x 0 (если это предель-

ное положение существует). Нормалью назовем прямую, проходящую через данную точку перпендикулярно касательной. Пусть касательная образует с положительным направлением оси O x угол 0 , а секущая – ( x) .

Тогда по определению

lim tg ( x) lim		y	tg 0 ,
x 0	x 0	x

т.е. тангенс угла наклона касательной равен пределу отношения приращения функции к приращению аргумента.

Отвлечемся теперь от конкретных задач и для произвольной функции y f (x) дадим аргументу x приращение x . Тогда функция получит прира-

щение y f (x x) f (x) . Рассмотрим предел отношения приращения функции y к приращению аргумента x , когда приращение аргумента стремится к нулю, т.е.

lim y .

x 0 x

Если этот предел существует, то он называется производной функции f (x) в точке x и обозначается f (x) . Поскольку производная в точке x

128

является функцией x , то, чтобы подчеркнуть этот факт, пользуются терми-

ном производная функция ( f
		(x) – производная функция функции f (x) ,
кратко:		f (x) ).
	f (x) – производная

Согласно этому определению скорость движения точки есть производная пути по времени v(t) x (t) , плотность массы стержня – производ-

ная массы по координате (x) m (x) , а тангенс угла 0 между положительным направлением оси O x и касательной к графику функции в данной точке равен значению производной функции в этой точке f (x0 ) tg 0 .

18.2. Вычисление производных. Операция нахождения производной функции называется дифференцированием. Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Пример недифференцируемой в точке x 0 функции y | x | приведен на рис. 18.2

Рис. 18.2

Действительно, для этой функции имеем

lim	y	1 ,	lim	y	1 ,
x 0	x		x 0	x

а, значит, предел этого отношения не существует когда x 0 произволь-

ным образом.

Если производная в данной точке существует и конечна, т. е. отноше-

ния y	к x стремится к конечной величине, когда x 0 , то отсюда
следует,	что y 0 . Таким образом, дифференцируемая в данной точке

функция будет непрерывной в этой точке. Обратное утверждение не верно, как показывает приведенный выше пример (см. рис. 18.2). В точке x 0 функция y | x | непрерывна, но недифференцируема.

Итак, непрерывность функции в данной точке – необходимое условие её дифференцируемости. Другими словами, если функция дифференцируема в данной точке, то она непрерывна в этой точке. Ввиду важности этого утверждения приведём его формальное доказательство.

129