
цифровая фильтрация / лаб / 3 Синтез оптимальных по чебышеву КИХ-фильтров / lab work 3
.pdfЛабораторная работа №3
СИНТЕЗ ОПТИМАЛЬНЫХ ПО ЧЕБЫШЁВУ ЦИФРОВЫХ КИХ-ФИЛЬТРОВ
Цель работы: изучение оптимального по Чебышёву метода синтеза КИХ-фильтров, синтез цифровых низкочастотных, высокочастотных, полосовых и режекторных фильтров.
Краткая теория
1. Основные определения
Простота расчета коэффициентов передаточной функции КИХфильтров методом окон сопровождается получением фильтров, которые обладают рядом недостатков:
1.Расположение граничных частот синтезированного фильтра не соответствует заданным на него спецификациям.
2.Пульсации в различных полосах фильтра аппроксимируются одинаково.
3.Ошибка аппроксимации, то есть разница между идеальной и реальной частотной характеристикой фильтра, распределена неравномерно по различным частотным полосам. Причем пульсации АЧХ фильтра возрастают при приближении к границам соответствующих полос. Необходимо отметить, что равномерное распределение пульсаций АЧХ в различных полосах фильтра, позволяет значительно снизить его порядок.
В теории цифровой обработки сигналов разработана методика, позволяющая устранить отмеченные выше недостатки синтезируемых цифровых фильтров. Однако она является достаточно сложной для понимания и требует программной реализации.
В классе КИХ-фильтров с линейной ФЧХ, существует возможность получить множество условий, для которых доказывается, что решение задачи синтеза цифровых фильтров является оптимальным по Чебышёву, то есть оптимальным в смысле минимума максимальной ошибки аппроксимации (иногда называемой минимаксной ошибкой или ошибкой Чебышёва). Фильтры, обладающие свойством оптимальности, отмеченным выше, называются фильтрами с равномерными (равноволновыми) пульсациями, поскольку ошибка аппроксимации данного типа фильтров является равномерно распределенной по его частотным полосам. Как следствие последнего, цифровые фильтры,
74
оптимальные в смысле минимума максимальной ошибки аппроксимации, будут иметь более низкий порядок, чем цифровые фильтры, синтезированные с использованием метода окон, при одинаково заданных спецификациях на синтез фильтров.
Далее будет сформулирована задача синтеза оптимальных фильтров в смысле минимума максимальной ошибки аппроксимации и проанализировано общее число максимумов и минимумов амплитудной характеристики КИХ-фильтров с линейной ФЧХ. С использованием этой формулировки может быть рассмотрен обобщенный алгоритм синтеза КИХ-фильтров с равномерными пульсациями, использующий полиномиальную интерполяцию при нахождении оптимального решения. Этот алгоритм получил название алгоритма ПарксаМакклеллана, включающий в себя алгоритм замены Ремеза для полиномиальных решений.
2. КИХ-фильтры с линейной ФЧХ
Фильтры с линейной ФЧХ могут быть классифицированы на 4 типа в зависимости от симметрии или антисимметрии импульсной характеристики h(n), а также четности или нечетности N . Каждый из этих типов имеет собственные ограничения на расположение нулей передаточной функции H(z), которая в свою очередь накладывает ограничения на характер частотной характеристики:
H(e jˆ ) e j e jNˆ / 2A(ˆ),
где – константа, зависящая от типа КИХ-фильтра с линейной ФЧХ, A(ˆ) – амплитудная характеристика, представляющая собой действительную функцию частоты ˆ [рад] и принимающая как положительные, так и отрицательные значения. Модуль амплитудной характеристики есть АЧХ КИХ-фильтра с линейной ФЧХ.
2.1. Фильтры типа I – симметричная импульсная
характеристика, N – четное
Центр симметрии импульсной характеристики проходит в точкеN /2. Частотная характеристика фильтра типа I с линейной ФЧХ выражается следующим образом:
75

|
|
H(e jˆ ) e jNˆ |
/ 2 |
N / 2 |
|
|
|||
|
|
a(k)cos(kˆ), |
|||||||
|
|
|
|
|
|
|
k 0 |
|
|
N |
|
|
N |
|
|
|
N |
||
где a(k) 2h |
|
k , |
k 1, 2, ..., |
|
|
, |
a(0) h |
|
. |
2 |
2 |
|
|
||||||
|
|
|
|
|
|
2 |
|||
Амплитудная характеристика имеет следующий вид:
N / 2
A(ˆ) a(k)cos(kˆ).
k0
2.2.Фильтры типа II – симметричная импульсная характеристика, N – нечетное
Центр симметрии импульсной характеристики проходит в точкеN /2. Частотная характеристика фильтра типа II с линейной ФЧХ может быть представлена в виде
H(e jˆ ) e |
jNˆ / 2 |
(N 1)/ 2 |
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|||||||||||
b(k)cos |
|
k |
|
ˆ |
, |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N 1 |
|
|
|
N 1 |
|
|
|
|
|
|
|
||||
где b(k) 2h |
|
|
k , |
k 1, 2,..., |
|
|
|
. |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Амплитудная характеристика имеет следующий вид:
|
(N 1)/ 2 |
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
A(ˆ) |
|
b(k)cos |
|
k |
2 |
ˆ |
. |
|
|
k 1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Последнее выражение может быть представлено в виде:
ˆ |
(N 1) / 2 |
~ |
|||
A(ˆ) cos |
|
|
|
|
b(k)cos(kˆ), |
2 |
|
||||
|
|
|
k 0 |
|
|
где коэффициенты b~(k) являются линейно связанными с коэффициентами b(k). Можно показать, что эта взаимосвязь имеет следующий вид:
b~(0) 1b(1), 2
76
b~(k) 2b(k) b~(k 1), |
k 1, 2,..., |
N 3 |
, |
|||||||
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
~ |
N 1 |
|
1 |
|
|
N 1 |
||||
b |
|
|
|
|
|
b |
|
. |
||
2 |
2 |
|
2 |
|||||||
|
|
|
|
|
|
|||||
2.3. Фильтры типа III – антисимметричная импульсная
характеристика, N – четное
Центр антисимметрии импульсной характеристики проходит в точке N /2. Частотная характеристика фильтра типа III с линейной ФЧХ может быть представлена в виде:
|
|
H(e jˆ ) je jNˆ / 2 |
N / 2 |
||||
|
|
c(k)sin(kˆ), |
|||||
|
|
|
|
|
|
|
k 1 |
N |
|
|
|
N |
|
|
|
где c(k) 2h |
|
k , |
k 1, 2, ..., |
|
|
. |
|
|
2 |
|
|||||
2 |
|
|
|
|
|||
Амплитудная характеристика имеет следующий вид: |
|||||||
|
|
|
|
N / 2 |
|
||
|
|
|
A(ˆ) c(k)sin(kˆ). |
||||
|
|
|
|
|
k 1 |
|
|
Последнее выражение может быть представлено в виде:
|
(N 2)/ 2 |
A(ˆ) sin(ˆ) |
c~(k)cos(kˆ), |
|
k 0 |
где коэффициенты коэффициентами c(k
следующий вид:
~ |
|
|
являются |
|
|
линейно |
связанными с |
|||||||
c(k) |
|
|
|
|||||||||||
). Можно показать, |
что эта |
взаимосвязь имеет |
||||||||||||
~ N 2 |
|
|
N |
|
|
|
|
|||||||
c |
|
|
|
|
c |
|
|
|
, |
|
|
|||
|
2 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
~ N 4 |
|
N 2 |
|
|
||||||||||
c |
|
|
|
|
c |
|
|
|
|
|
, |
|
||
|
2 |
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
77
~ |
~ |
|
|
|
N 4 |
||
c |
(k 1) c(k 1) 2c(k), |
2 k |
|
, |
|||
2 |
|||||||
|
|
|
|
|
|
||
|
~ |
1 ~ |
|
|
|
||
|
c(0) |
|
c(2) c(1). |
|
|
||
|
2 |
|
|
||||
|
|
|
|
|
|
||
2.4. Фильтры типа IV – антисимметричная импульсная
характеристика, N – нечетное
Центр антисимметрии импульсной характеристики проходит в точке N /2, при этом не является целым числом. Частотная характеристика фильтра типа IV с линейной ФЧХ может быть представлена в виде
H(e jˆ ) je |
jNˆ / 2 |
(N 1)/ 2 |
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|||||||||||
d(k)sin |
|
k |
|
ˆ |
, |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N 1 |
|
|
|
N 1 |
|
|
|
|
|
|
|
||||
где d(k) 2h |
|
|
k , |
k 1, 2, ..., |
|
|
|
. |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Амплитудная характеристика имеет следующий вид:
|
(N 1)/2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
A(ˆ) |
|
d(k)sin |
k |
2 |
ˆ |
. |
|
|
k 1 |
|
|
|
|
|
|
Последнее выражение может быть представлено в виде:
ˆ |
|
(N 1)/2 |
||
~ |
||||
A(ˆ) sin |
|
|
|
d(k)cos(kˆ), |
2 |
|
|||
|
|
|
k 0 |
|
где коэффициенты d~(k) являются линейно связанными с коэффициентами d(k). Можно показать, что эта взаимосвязь имеет следующий вид:
~ |
N 1 |
|
N 1 |
|
|
|
|||
d |
|
|
2d |
|
|
, |
|
|
|
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||
d~(k 1) d~(k) 2d(k), |
2 k |
N 1 |
, |
||||||
|
|||||||||
|
|
|
|
|
|
2 |
|
||
78

d~(0) 1 d~(1) d(1). 2
В заключение рассмотренного выше необходимо отметить, что общее выражение для представления амплитудных характеристик КИХфильтров с линейной ФЧХ может быть записано в виде:
A(ˆ) Q(ˆ)P(ˆ),
где выражения для Q(ˆ) и P(ˆ) приведены в табл. 1.
Q( ), L, P( ) для КИХ-фильтров с линейной ФЧХ |
Таблица 1 |
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тип КИХ-фильтра |
Q(ˆ) |
|
|
|
|
L |
|
|
P(ˆ) |
||||
с линейной ФЧХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
тип 1 |
1 |
|
|
|
|
|
|
N |
|
L |
|
||
|
|
|
|
|
|
|
|
|
a(n)cos(kˆ) |
||||
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
k 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тип 2 |
ˆ |
|
|
|
N 1 |
|
L ~ |
||||||
cos |
|
|
|
|
|
|
|
|
|
b |
(n)cos(kˆ) |
||
|
|
2 |
|
||||||||||
|
|
|
|||||||||||
|
2 |
|
|
|
|
k 0 |
|
||||||
|
sin ˆ |
|
N 2 |
|
L |
|
|||||||
тип 3 |
|
|
|
|
|
|
c~(n)cos(kˆ) |
||||||
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
k 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тип 4 |
ˆ |
|
|
|
N 1 |
|
L ~ |
||||||
sin |
|
|
|
|
|
|
|
|
|
d |
(n)cos(kˆ) |
||
|
|
|
2 |
|
|||||||||
|
|
||||||||||||
|
2 |
|
|
|
|
k 0 |
|
||||||
Замечание. В настоящей работе рассматривается синтез линейных цифровых частотно-избирательных КИХ-фильтров (ФНЧ, ФВЧ, ПФ, РФ) с линейной ФЧХ.
3. Теорема чередования
Для дальнейшего рассмотрения материала помимо функции, описывающей амплитудную характеристику A(ˆ) реального фильтра, введем функцию, описывающую амплитудную характеристику Aи(ˆ) идеального фильтра и весовую функцию W(ˆ), регулирующую относительный размер ошибки аппроксимации в различных частотных полосах синтезируемого фильтра. Амплитудная характеристика Aи(ˆ) идеального фильтра принимает значение 1 в ПП фильтра и значение 0 в ПЗ для класса частотно-избирательных фильтров (ФНЧ, ФВЧ, ПФ, РФ). Весовую функцию W(ˆ) необходимо выбирать так, чтобы
79

существовала возможность независимого контроля ошибки аппроксимации в различных частотных полосах фильтра. Например, для ФНЧ весовая функция W(ˆ) может быть выбрана в следующем виде:
|
з |
, для ПП, |
||
|
|
|
||
п |
||||
W(ˆ) |
(1) |
|||
|
|
|
для ПЗ, |
|
1, |
|
|||
где п – отклонение АЧХ от 1 в ПП, з – отклонение АЧХ от 0 в ПЗ. Определив амплитудные характеристики реального и идеального
фильтров, а так же весовую функцию, введем в рассмотрение взвешенную ошибку аппроксимации:
E(ˆ) W(ˆ)[Aи(ˆ) A(ˆ)]
W(ˆ)[Aи(ˆ) Q(ˆ)P(ˆ)]
W(ˆ)Q(ˆ) Aи (ˆˆ) P(ˆ) .
Q( )
Для удобства введем модифицированную весовую функцию Wˆ (ˆ) и модифицированную амплитудную характеристику идеального фильтра Aˆи(ˆ) в виде:
Wˆ (ˆ) W(ˆ)Q(ˆ),
Aˆи(ˆ) Aи(ˆ) .
Q(ˆ)
Тогда взвешенная ошибка аппроксимации для четырех типов КИХфильтров с линейной ФЧХ может быть представлена в виде:
E(ˆ) Wˆ (ˆ)[Aˆи(ˆ) P(ˆ)].
В результате процедура расчета цифрового фильтра заключается в нахождении коэффициентов фильтра (k), которые минимизируют максимум абсолютной ошибки аппроксимации E(ˆ):
|
|
|
|
|
|
Wˆ(ˆ)[Aˆи (ˆ) |
L |
|
|
min |
E(ˆ) |
min max |
(k)cos(kˆ)] |
, (2) |
|||||
max |
|
||||||||
(k) ˆ S |
|
|
(k) ˆ |
S |
|
k 0 |
|
||
|
|
|
|
|
|
|
|
||
где S – совокупность интервалов аппроксимации. По существу S содержит множество полос пропускания и полос задерживания фильтра.
80

Применительно к рассмотренной выше проблеме синтеза цифровых фильтров, Паркс и Макклеллан переформулировали теорему теории аппроксимации Чебышёва, получив в результате следующую формулировку.
Теорема чередования. Пусть S – любое замкнутое подмножество закрытого интервала 0 ˆ . Для того, чтобы функция P(ˆ), представимая в виде:
L
P(ˆ) (k)cos(kˆ) k 0
была единственной и наилучшей аппроксимацией на подмножестве S для функции Aˆи(ˆ), необходимо и достаточно, чтобы функция ошибки E(ˆ) имела на S , по крайней мере, L 2 чередований. То есть существует, по крайней мере, L 2 экстремальных частот ˆ i на подмножестве S , таких что ˆ1 ˆ 2 ˆ L 2, E(ˆi) E(ˆi 1) и
E(ˆi) maxE(ˆ) , i 1, 2, , L 2.
ˆ S
Для конкретизации теоремы чередования, рассмотрим синтез ФНЧ
с ПП 0 ˆ ˆ п и ПЗ ˆ з |
ˆ |
. Так как амплитудная характеристика |
||||||
идеального фильтра Aи(ˆ) и весовая функция W(ˆ) являются кусочно- |
||||||||
постоянными, можно записать |
|
|
|
|||||
|
dE(ˆ) |
|
|
d |
{W(ˆ)[A (ˆ) A(ˆ)]} |
|||
|
|
|
||||||
|
dˆ |
|
dˆ |
|
и |
|||
|
|
|
dA(ˆ) |
|
||||
|
|
W(ˆ) |
0. |
|||||
|
|
|
||||||
|
|
|
|
|
|
|
dˆ |
|
Поэтому частоты ˆ i, |
|
соответствующие пикам E(ˆ), также |
||||||
соответствуют пикам, в |
которых A(ˆ) удовлетворяет допускаемой |
|||||||
ошибке. Так как A(ˆ), например, для КИХ-фильтров типа 1 с линейной ФЧХ представляет собой тригонометрический полином степени L представимый в виде:
81

L
A( ) (k)cos(kˆ)
|
k 0 |
|
|
|
|
L |
k |
|
|
|
(k) nk (cos(ˆ))n |
|
(3) |
|
|
k 0 |
|
|
|
|
n 0 |
|
|
|
L
~ ˆ k
(k)(cos( )) ,
|
k 0 |
|
то A(ˆ) |
имеет не больше чем L 1 |
локальных максимумов и |
минимумов на открытом интервале 0 ˆ |
. Дополнительно можно |
|
отметить, что частоты ˆ 0 и ˆ обычно являются экстремумами амплитудной характеристики A(ˆ), а также взвешенной ошибки аппроксимации E(ˆ). Следовательно, функция A(ˆ) имеет не больше чем L 1 экстремальных частот. Кроме того, граничные частоты в ПП и ПЗ, ˆ п и ˆ з, также являются экстремумами функции E(ˆ), так как
E(ˆ) является максимальным на этих частотах. Следовательно, должно существовать L 3 экстремальных частот функции E(ˆ) для единственной и наилучшей аппроксимации идеального ФНЧ. С другой стороны теорема чередования устанавливает существование, по крайней мере, L 2 экстремальных частот E(ˆ). Таким образом, единственная и наилучшая аппроксимация для идеальной амплитудной характеристики фильтра Aи(ˆ) имеет либо L 2, либо L 3 чередований взвешенной ошибки аппроксимации E(ˆ). Синтезированные фильтры, содержащие L 3 чередований, были названы Парксом и Макклелланом фильтрами с дополнительной пульсацией. Последнее связано с тем фактом, что данного типа фильтры обладали большим, чем минимальное число L 2 чередований функции ошибки, требуемым для оптимальности.
Теорема чередования гарантирует единственность решения для достижения задачи оптимизации, представленной выражением (2). Из теоремы чередования следует, что для заданного множества экстремальных частот ˆ i можно записать:
Wˆ (ˆ i)[Aˆи(ˆ i) P(ˆ i)] ( 1)i , i 0,1, , L 1, (4)
где представляет максимальную величину взвешенной ошибки аппроксимации E(ˆ). Фактически, если весовая функция W(ˆ) выбрана так, как представлено в выражении (1), то з .
82
Множество линейных уравнений, представленных выражением (4), можно записать в виде:
P(ˆ i) |
( 1)i |
|
Aˆи (ˆ i), i 0,1, , L 1, |
|
|
|||
Wˆ(ˆ i) |
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
L |
|
( 1)i |
Aˆи(ˆi), |
|
|
|
||
(k)cos(kˆi) |
|
|
i 0,1, , |
L 1. |
(5) |
|||
Wˆ (ˆ |
) |
|||||||
k 0 |
|
i |
|
|
|
|
|
|
Выражение (5) может быть записано в матричной форме относительно неизвестных коэффициентов фильтра (k) и максимальной величины взвешенной ошибки аппроксимации E(ˆ):
|
cos(ˆ 0) |
1 |
|
|
|
|
cos(ˆ1) |
1 |
|
|
|
|
|
|
|
|
cos(ˆ L 1) |
1 |
|
|
|
|
cos(Lˆ 0) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Wˆ (ˆ 0) |
(0) |
|
|
Aˆ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
(ˆ |
0 |
) |
|
|
||||||||||
|
|
1 |
|
|
|
|
(1) |
|
|
|
и |
|
|
|
|
||||
|
cos(Lˆ1) |
|
|
|
|
|
|
|
|
|
|
Aˆ |
(ˆ |
|
) |
|
|
||
Wˆ (ˆ |
) |
|
|
|
. (6) |
||||||||||||||
|
|
|
|
|
|
|
|
|
и |
1 |
|
|
|
||||||
|
|
1 |
|
|
|
(L) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Aи |
(ˆ L 1) |
|
|||||||
|
cos(Lˆ L 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
W(ˆ L 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При заданных экстремальных частотах, выражение (6) можно решить относительно неизвестных коэффициентов фильтра (k) и максимальной величины взвешенной ошибки аппроксимации E(ˆ).
4. Алгоритм замены Ремеза
Рассматривая теорему чередования, необходимо сказать, что она гарантирует для минимаксной аппроксимации, представленной выражением (2), существование и единственность решения, однако она не дает никакого представления об алгоритме, с использованием которого оптимальное решение может быть получено. Паркс и Макклеллан предложили итерационную процедуру, основанную на алгоритме замены Ремеза и позволяющую найти оптимальное решение задачи минимаксной аппроксимации амплитудной характеристики фильтра. Данная процедура предполагает, что порядок фильтра N , граничные частоты ˆ п, ˆ з и отношение з 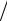 п являются известными. Однако является более естественным во время процедуры синтеза
п являются известными. Однако является более естественным во время процедуры синтеза
83
