МАТ_АНАЛІЗ_1_курс_2_семестр_Інтэграл_2

lim

x

x

x

f (x) .

x

x 0

Разгледзім рознасць

x x

x

x

x

x

f t

dt

f t

dt

a

a

x

x x

x

x

x

f t dt

f t dt

f t dt

f t dt .

a

x

a

x

Адсюль, скарыстаўшы тэарэму аб сярэднім значэнні, атрымаем, што

x x

f t

dt

f

x ,

x

дзе пункт ξ ляжыць паміж x і x

x . Заўважым, што, калі x

0 , то

x .

Улічваючы ўсё адзначанае вышэй, будзем мець:

lim

x

x

x

lim

f

x

lim f

limf

f

x ,

x

x

x 0

x

0

x 0

x

бо дадзеная функцыя непарыўная ў кожным пункце х адрэзка

a, b . Тэарэму

даказалі.

Заўвага. З даказанай тэарэмы вынікае, што, калі функцыя f

x

непарыўная на

адрэзку a, b , то

x

таксама непарыўная на дадзеным

a, b адрэзку.

Адзначым,

што непарыўнасць

x можа быць даказанай пры больш слабых

меркаваннях, менавіта, пры меркаванні інтэгравальнасці f (x)

на f x

адрэзку

a, b .

Існаванне першаіснай для непарыўнай функцыі.

Тэарэма 2. Калі функцыя f x непарыўная на адрэзку , то на гэтым адрэзку

для яе існуе першаісная.

Доказ. Сапраўды, згодна з тэарэмай 1 такой першаіснай будзе функцыя

x

x f t dt .

a

Лекцыя 4

Формула Ньютана-Лейбніца. Замена зменнай	i
інтэграванне па частках у вызначаным інтэграле.
Формула Ньютана-Лейбніца.

Няхай функцыя f	x непарыўная на адрэзку a, b ; F				x — якая-небудзь яе
першаісная на	гэтым адрэзку. Тады мае месца				наступная формула:
b			ab
f x dx F b F a F x				,
a

якая называецца формулай Ньютана-Лейбніца.

2

Прыклад.

1.

sin x dx

cos x

2

cos

cos

cos0

0

0

2

2

Дакажам формулу Ньютана-Лейбніца.

Тэарэма 4.1. Няхай функцыя f

x

непарыўная на адрэзку

a, b

і

— якая-

x

небудзь

першаісная

функцыі

f

x .

Функцыя

x

f t

dt

таксама

a

з’яўляецца першаіснай для функцыі . Паколькі дзве першаісныя для функцыі адрозніваюцца на канстанту, то

x	F x		C ,			(4.1)
дзе С — канстанта.
Калі ў роўнасць (1) падставіць x					a , то будзем мець:
a	F a		C .
			a
Паколькі		a	f t dt	0 , вынікае, што C F a . Таму роўнасць (4.1)
			a
можна запісаць у выглядзе:				x	F x	F a .
Калі ў апошнюю роўнасць падставіць x						b , то атрымаем:
b	F b		F a ,
	b
г. зн.	f x dx F b F a .

a

Замена зменнай i інтэграванне па частках у вызначаным інтэграле.

Тэарэма 4.2. Няхай функцыі u x , v x непарыўныя на адрэзку a, b і маюць на гэтым адрэзку непарыўныя вытворныя u ' x , v ' x . Тады мае месца наступная формула:

b			b
u dv uv		ab	v du ,	(4.2)
a			a

якая называецца формулай інтэгравання часткамі.

Прыклад.

u

x

cos x

dv

2

2

x cos x dx

x sin x

2

sin x dx

x sin x

2

cos x

2

1

0

du

dx

0

0

0

0

2

v

sin x

.

Дакажам формулу (4.2). Як вядома,

uv

' u 'v

uv ' , г.

зн. функцыя

uv

з’яўляецца першаіснай функцыі u 'v

uv '.

Скарыстаўшы формулу Ньютана-

Лейбніца, будзем мець:

b

ab ,

u 'v

uv ' dx uv

a

b

b

ab ,

vu 'dx

uv 'dx

uv

aa

bb

v du	u dv			uv		ab ,
a	a
b			ab	b
u dv	uv			v du .
a				a
Тэарэма 4.3. Няхай функцыя f x непарыўная на адрэзку							a, b , а функцыя
t вызначаная і непарыўная разам са сваёй вытворнай							' t на адрэзку

,, прычым

a t b

t	.
Тады мае месца наступная роўнасць:
b
f x dx	f	t	' t dt .	(4.3)

a

Формула (4.3) называецца формулай замены зменнай (падстаноўкі) у вызначаным інтэграле.

Доказ. Адзначым, што непарыўнасць функцый f x ,		t	,	'	t	забяспечвае
існаванне інтэгралаў у формуле (1). Дакажам роўнасць гэтых інтэгралаў.
Паколькі функцыя f	x з’яўляецца непарыўнай на адрэзку			a,	b , то на гэтым
адрэзку яна мае першаісную. Абазначым яе праз F		x .	Мяркуем x				t .
Тады функцыя F	t будзе першаіснай для функцыі f		t		'	t .

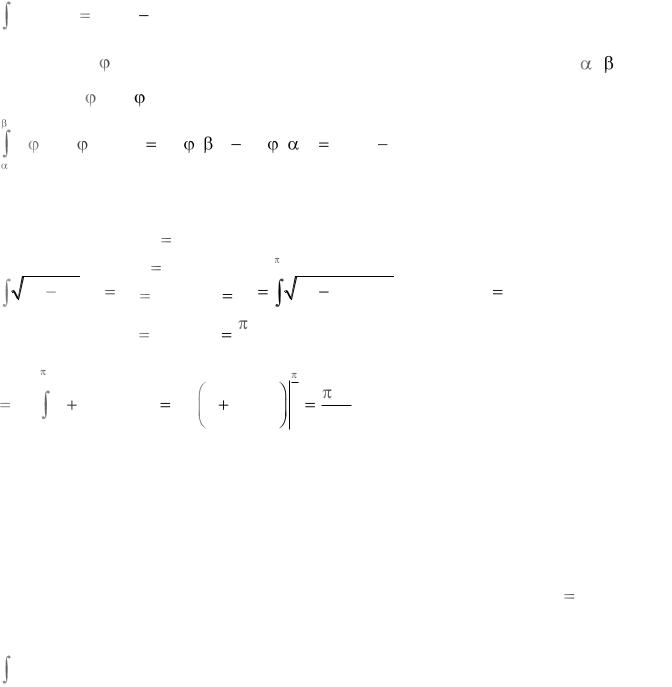
Функцыя F x з’яўляецца першаіснай для непарыўнай на адрэзку a, b

функцыі f x , таму па формуле Ньютана-Лейбніца маем:

b

f x

dx

F

b

F

a .

(4.4)

a

Функцыя F

t

з’яўляецца першаіснай для непарыўнай на адрэзку ,

функцыі f

t

' t , таму па формуле Ньютана-Лейбніца маем:

f

t

' t

dt

F

F

F b F a . (4.5)

З роўнасцяў (4.4) і (4.5) вынікае роўнасць (4.3).

Прыклад.

x

a sint

a

dx

a cost dt

2

a2

x2 dx

x

0 пры t 0

a2 a2 sin2 t a cos t dt

0

0

x

a пры t

2

a2 2				a2		sin2t
			1 cos 2t dt		t
2 0				2		2

2 a2

0 4

.

Лекцыя 5

Набліжанае вылічэнне вызначаных інтэгралаў (формулы прамавугольнікаў, трапецый, Сімпсана).

Няхай на адрэзку a, b зададзена інтэгравальная функцыя y f x .

Разгледзім пытанне вылічэння вызначанага інтэграла

b

f x dx .

a

Дакладнае значэнне вызначанага інтэграла не заўсёды можна знайсці. У выпадку, калі дакладнае значэнне інтэграла знайсці складана, яго вылічваюць набліжана. Гэта можна зрабіць пры дапамозе так званых квадратурных формул. З прасцешымі з гэтых формул і пазнаёмімся ў дадзеным параграфе.

Квадратурная формула прамавугольнікаў

Рыс. 44

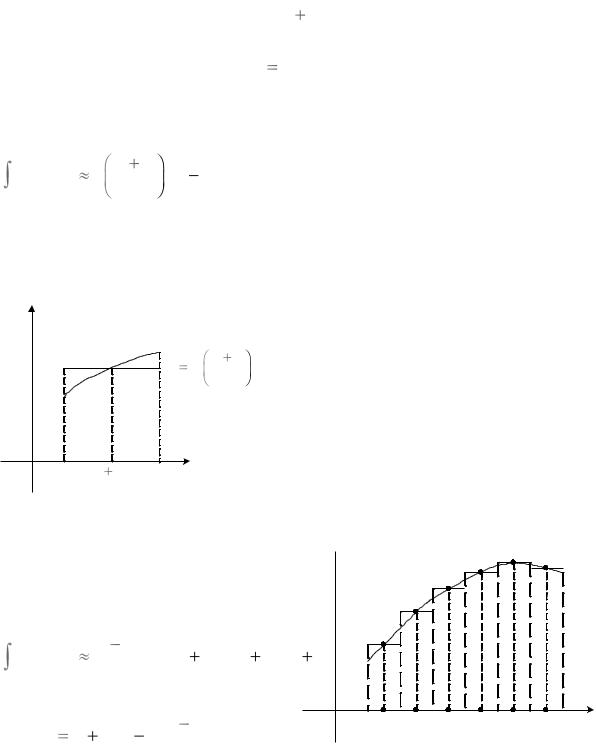
Падынтэгральную функцыю f x	заменім мнагаскладам нулявой ступені, які су-
падае з дадзенай функцый у пункце		a	b	(рыс. 43).
			2
У выпадку, калі функцыя y		f	x непарыўная і неадмоўная на адрэзку

a, b , гэта сведчыць аб тым, што плошчу крывалінейнай трапецыі замяняем

плошчай прамавугольніка. Пры гэтым атрымліваем набліжаную роўнасць

	b	a b
	f x dx f		b a . (1)
		2
	a

Набліжаная роўнасць (1) называецца квадратурнай формулай прамавугольнікаў.

Калі адрэзак a, b разбіць на n роўных частак і на кожным частковым адрэзку

y

y f(x)

	y f	a b
		2

O a	a	b	b x

2

Рыс. 43

скарыстаць квадратурную формулу прамавугольнікаў (1), то атрымаем абагульненую формулу прамавугольнікаў (рыс. 44):

	b		b a
	f x	dx		f x		f		x
									2
			n	1
	a
	,			(2)
	дзе xk	a	2k	1	b	a		(k = 1, 2,
					2n

y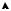

f xn

O

a x1 x2

xk

xn b x

… , n).

Абагульненную формулу прамавугольнікаў коратка называюць таксама формулай прамавугольнікаў.

Пры карыстанні квадратурнай формулай важна ведаць рознасць паміж дакладным набліжаным значэннем інтэграла. Гэта рознасць называецца астачай або хібнасцю квадратурнай формулы.

Калі функцыя				f x		на адрэзку a, b	мае непарыўную другую вытворную
f	x	, то астача R f				абагульненай формулы прамавугольнікаў роўная
R	f		b a	3	f	,	(3)
			24n2
дзе			a, b .

Квадратурная формула трапецый

y

		)
	x
	(
y	f

O	a	b	x
Рыс. 45
Падынтегральную функцыю f				x заменім мнагаскладам, ступень якога меншая
або	роўная 1,	які супадае з дадзенай функцыяй у пунктах a і b
(рыс. 45).
У выпадку, калі функцыя f			x	непарыўная і неадмоўная на адрэзку a, b , гэта

сведчыць аб тым, што плошчу крывалінейнай трапецыі замяняем плошчай трапецыі. Пры гэтым атрымаем набліжаную роўнасць

	b	b a
	f x dx		f a f b .	(4)
		2
	a

Дадзеная набліжаная роўнасць называецца квадратурнай формулай трапецый.

Калі адрэзак a, b падзяліць на n роўных частак і на кожным частковым адрэзку скарыстаць квадратурную формулу (4), то атрымаем абагульненую

y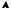

O a x1 x2

xn b xn 1 x

Рыс. 46

формулу трапецый

b

f

x dx

a

(5)

b a

f x 2 f x

f x

f x

,

2

n

n 1

2n

1

дзе xk

a

k

1

b

a

( k = 1, 2, … , n+1) (рыс. 46).

n

Калі функцыя f

x

на адрэзку a,

b мае непарыўную другую вытворную, то

астача R f

квадратурнай формулы (5) роўная

R

f

b a

3

f

,

(6)

12n2

дзе

a,

b .

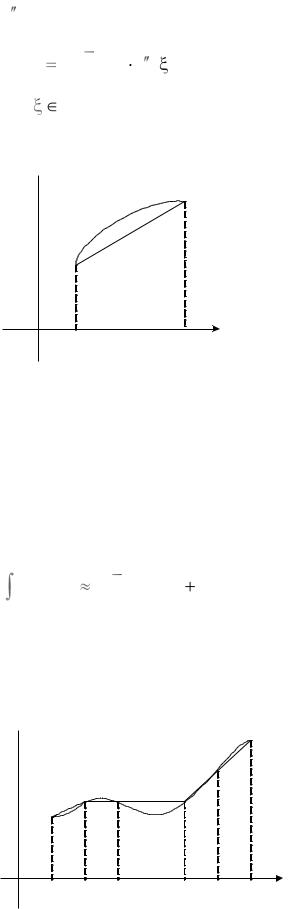
Квадратурная формула Сімпсана

Падынтэгральную функцыю

f

x

заменім

y

мнагаскладам y

Ax2

Bx

C ,

ступень

y=Ax2+Bx+C

якога меншая або роўная 2, які супадае з

дадзенай функцыяй у пунктах a, b i

a

b

y

f(x)

2

(рыс. 47).

У выпадку, калі функцыя f x

непарыўная і

неадмоўная на адрэзку, гэта сведчыць аб

O

a

a+b

b x

тым, што плошчу крывалінейнай трапецыі,

2

Рыс. 47

абмежаванай

графікам

функцыі

f

x

,

замяняем

плошчай

крывалінейнай

трапецыі,

абмежаванай

парабалай

y

Ax2 Bx

C . Атрымаем роўнасць

b

b

f

x

dx

Ax2 Bx

C

dx ,

a

a

b

x3

x2

b

г. зн.

f x dx A

B

Cx

,

a

3

2

a

b

A

B

г. зн.

f x dx

b3

a3

b 2 a2

C b a ,

a

3

2

b

b

a

г. зн.

f

x

dx

2A b2

ab

b2

3B b a

6С .

(7)

6

a

Знойдзем правую частку роўнасці (7), скарыстаўшы той факт, што мнагасклад

y

Ax2

Bx

C супадае з функцыяй f

x

у пунктах a,

a

b

і b.

2

Маем f a

Aa2

Ba

C , f

a

b

A

a b 2

B

a

b

C ,

2

2

2

f b

Ab2

Bb

C .

З апошніх трох роўнасцяў вынікае

f a 4f

a b

f b 2A b2

ab b2

3B b a 6С .

2

Падставім знойдзены выраз у роўнасць (7) і будзем мець, што

b

b

a

a

b

f

x dx

f a

4f

f

b

.

(8)

6

2

a

Набліжаная роўнасць (8) называецца квадратурнай формулай Сімпсана.

Калі адрэзак a, b падзяліць на n частак ( n — цотны лік) і на парах частковых адрэзкаў скарыстаць формулу Сімпсана, то атрымаем абагульненую формулу Сімпсана

b		b a
f x dx			f x	4 f x		f x		f x
					2		4		n
		3n	1
a
2 f x3	f x5 f			xn 1		f xn 1 ,			(9)

дзе xk a

Калі функцыя

то астача R f

k	1	b a	( k = 1, 2, … , n+1), n — цотны лік.
		n
f	x на адрэзку a, b мае непарыўную чацвёртую вытворную,
	квадратурнай формулы Сімпсана (9) роўная

	R f	b a	5	f 4	,
		180n4
	дзе	a, b .

Лекцыя 6

Няўласны інтэграл з бясконцымі лімітамі інтэгравання (няўласныя інтэгралы першага роду).

Няўласныя інтэгралы першага роду

Разгледзім прыклады, якія прыводзяць да такіх інтэгралаў.

	Прыклад 1. Знайсці плошчу Р пад крывой y	1	, x a 0	(рыс. 6.1).
		x

Рашэнне. Плошчу ўсёй заштрыхаванай фігуры непасрэдна вылічыць складана. Аднак, калі адсекчы бясконцы «хвост» прамой x b , то плошчу крывалінейнай

трапецыі aABb можна знайсці пры дапамозе вызначанага інтэграла b dx . Пры

a x

b

P lim

b

мы павінны атрымаць плошчу Р ўсёй заштрыхаванай фігуры, г. зн.

b dx		lim ln		x			b	lim ln b lna	.
a	x						a
		b						b

Такім чынам, у дадзеным выпадку няма сэнсу весці размову пра плошчу.

Прыклад 2. Знайсці плошчу Р пад крывой y x12 , x a 0 .

Рашэнне. Калі разважаць аналагічным чынам, як і ў прыкладзе 1, будзем мець

P

lim

b dx

lim

1

b

lim

1

1

1

.

2

b

a x

b

x

a

b

b

a

a

1

Значыць, у дадзеным выпадку плошча бясконцага «хваста» роўная

.

a

Азначэнне 1. Няхай функцыя f

x

непарыўная на прамежку a,

. Тады

b

канечны

ліміт

lim

f

x

dx

(калі ён

існуе)

будзе называцца

няўласным

b

a

інтэгралам першага роду і абазначыцца

f

x

dx .

a

Такім чынам,

b

f

x dx

lim

f

x dx .

(1)

a

b

a

y

A

y

1

x

B

O

a

b

x

Рыс. 6.1

Аналагічна вызначаюцца наступныя няўласныя інтэгралы:

b				b
f	x	dx	lim	f	x	dx ,	(2)
			a	a
			c
f	x	dx	f	x	dx	f x dx .	(3)

c

Калі існуе канечны ліміт (1), то гавораць, што няўласны інтэграл (1) збягаецца. Калі ж ліміт (1) не існуе або бясконцы, то гавораць, што няўласны інтэграл разбягаецца.

	Напрыклад, няўласны інтэграл	dx	у прыкладзе 1 разбягаецца,
		x
	a

dx

а няўласны інтэграл a x 2 з прыкладу 2 збягаецца.

Адзначым, што няўласны інтэграл у левай частцы роўнасці (3) збягаецца тады, калі збягаецца кожны з няўласных інтэгралаў у правай частцы.

Прыклад 3. Вылічыць

dx

.

1 x2

Рашэнне.

dx

0

dx

dx

0

dx

b

dx

lim

lim

1 x

2

1 x

2

1 x

2

a 1 x

2

0 1 x

2

0

a

b

lim arctg x		a0	lim arctg x		0b	lim arctg a	lim arctg b				.
								2	2
a			b			a	b
г. зн. дадзены інтэграл збягаецца.

Вельмі часта, калі неабходна вызначыць, збягаецца або разбягаецца няўласны інтэграл, невылічваючы яго значэння, карыстаюцца наступнымі прыметамі збежнасці.

Тэарэма 1. Няхай пры x	a 0 f x	x . Калі	x	dx збягаецца, то
			a
збягаецца і інтэграл f x	dx , прычым	x dx	f	x dx .
a		a	a
Калі f x dx разбягаецца, то разбягаецца і няўласны інтэграл					x dx .

a

a