МАТ_АНАЛІЗ_1_курс_2_семестр_Інтэграл_3

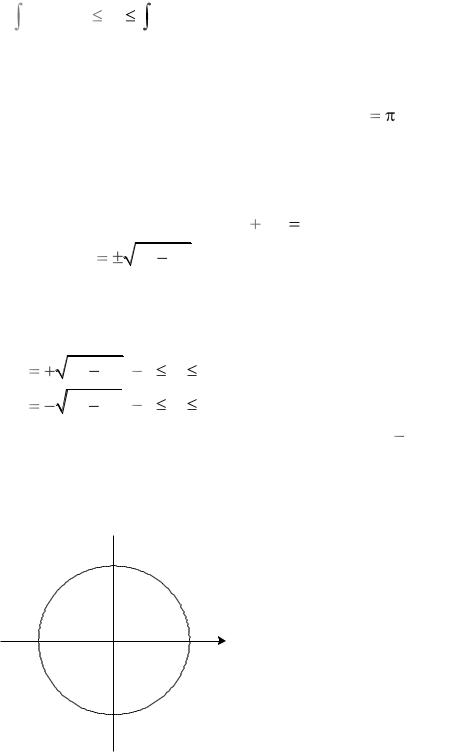
b	b
f x dx P	f x dx .
a	a

Адсюль і вынікае роўнасць (16).

Прыклад 3. Разгледзім круг радыуса r. Дакажам, што ён з’яўляецца

квадравальнай фігурай і яго плошча роўная P

r 2 .

Доказ. Разгледзім круг радыўса r. Пабудуем прамавугольную сістэму каардынат, каб яе пачатак супадаў з цэнтрам круга (рыс. 1.7).

У гэтай сістэме каардынат акружнасць, якая з’яўляецца граніцай дадзенага круга, задаецца раўнаннем x2 y 2 r 2 .

Адсюль: y

r 2 x2 .

Знак «+» адпавядае верхняй паўакружнасці, «–» — ніжняй паўакружнасці. Граніца дадзенага круга складаецца з дзвюх частак (дзве паўкружнасці), раўнанні якіх маюць выгляд:

y	r 2	x2	,	r	x	r ,
y	r 2	x2	,	r	x	r .

Паколькі гэтыя функцыі непарыўныя на адрэзку r, r , то на падставе тэарэмы

2 можам сцвярджаць, што круг з’яўляецца квадравальнай фігурай.

Вылічым цяпер плошчу дадзенага круга. Спачатку вылічым плошчу P1 y

r

O

x

Рыс. 1.7

чацвёртай часткі круга. Скарыстаўшы формулу (16), будзем мець:

				x	r cost
r			dx		r sint dt
P	r 2 x2 dx
1			x	0 пры t
0						2
			x	r	пры t 0

r	2	2	1 cos 2t		dt	r	2	.
		0		2		4

0

r 2 sin2 t dt

2

Калі цяпер скарыстаць уласцівасці інварыянтнасці і адытыўнасці плошчы, то атрымаем, што плошча круга роўная P r 2 .

Прыклад 4. Разгледзім кругавы сектар радыуса r, які адпавядае вуглу

(рыс. 1.8).

Рыс. 1.8

Рашэнне.Кругавы сектар — квадравальная фігура (гл. тэарэму 2). Вылічым плошчу кругавога сектара. Для зручнасці будзем лічыць, што 0 2 .

Маем:

r cos

r

P

x tg

dx

r 2

x2 dx

0

r cos

x2

tg

r cos

r

2

0

sin

2

t dt

1

r

2

.

2

0

2

Заўвага 1. Няхай функцыя y

f

x вызначана на адрэзку a, b . Мяркуем, што

функцыя f x

з’яўляецца непарыўнай на дадзеным адрэзку, дзе f x 0 .

Разгледзім фігуру, якая абмежавана графікам дадзенай функцыі і прамымі x a , x b , y 0 (рыс. 1.9).

Гэта фігура з’яўляецца квадравальнай (тэарэма 2). Вылічым яе плошчу P.

З гэтай мэтай пабудуем крывалінейную трапецыю, абмежаваную прамымі x a , x b , y 0 і графікам функцыі y f x . Плошчу пабудаванай

крывалінейнай трапецыі можна вылічыць па формуле (16):

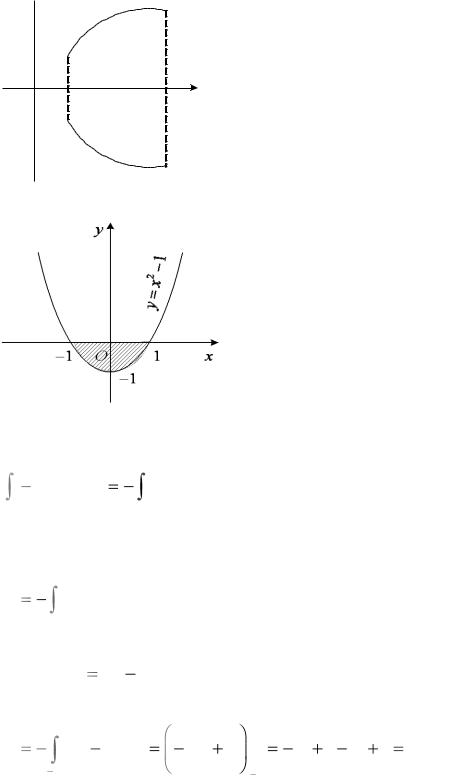
y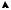 y f(x)

O a

b x

y f(x)

Рыс. 1.9

Рыс. 1.10

b	b
f x dx	f x dx .
a	a

Калі скарыстаць уласцівасць інварыянтнасці плошчы, то атрымаем наступную формулу для вылічэння плошчы разглядаемай плоскай фігуры:

	b
P	f x dx .	(18)

a

Прыклад 5. Вылічыць плошчу фігуры, якая абмежавана воссю Ox і графікам функцыі y x2 1 (рыс. 1.10).

Рашэнне. Скарыстаўшы формулу (18), атрымаем:

		1	x3			1
	P	x2 1 dx		x
			3
		1				1

	1	1	1	1	4	(кв. адз.).
	3		3		3

Заўвага 2. Падчас неабходна вылічыць плошчу фігуры, абмежаванай графікам функцыі, якая непарыўная на некаторым адрэзку і мяняе знак у канечным ліку пунктаў гэтага адрэзка. Вылічэнне плошчы ў гэтым выпадку зводзіцца да выкарыстання формул (16) і (18), а таксама ўласцівасці адытыўнасці плошчы.

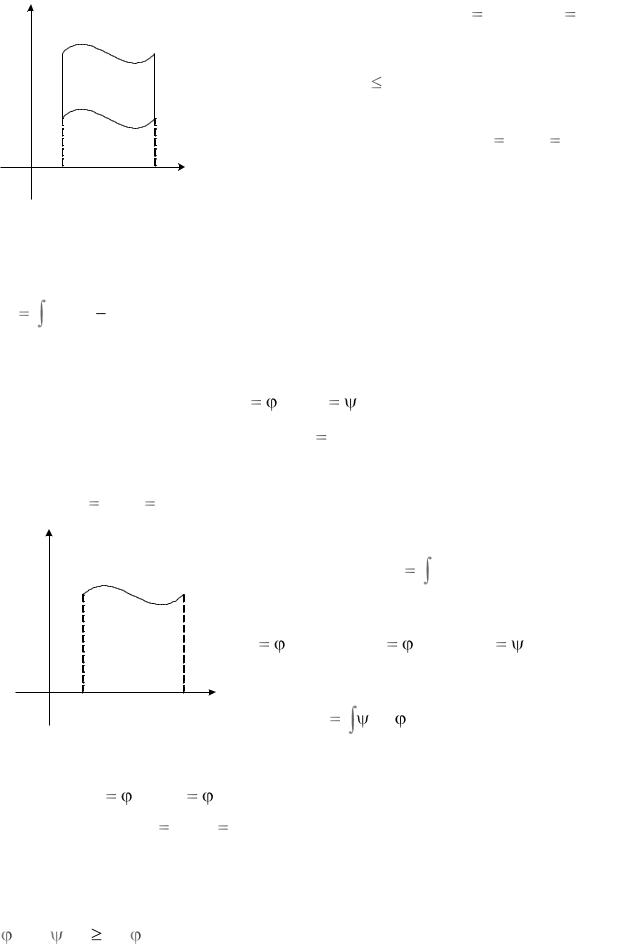
y	y	f2(x)		Заўвага 3. Няхай функцыі			y	f1 x і y		f2 x
				вызначаныя	і	непарыўныя		на	адрэзку	a, b ,
				прычым f1	x	f2 x	на		гэтым адрэзку.
				Разгледзім фігуру, якая абмежавана графікамі
	y	f1(x)		дадзеных функцый і прамымі x					a , x	b (рыс.
O	a		b x	24).
				Гэта фігура з’яўляецца квадравальнай (тэарэма
	Рыс. 1.11			2). Вылічым яе плошчу P. Карыстаючыся фор-

мулай (16) і ўласцівасцю адытыўнасці плошчы, атрымаем наступную формулу для вылічэння плошчы разглядаемай фігуры:

b

P

f2 x

f1 x

dx .

(19)

a

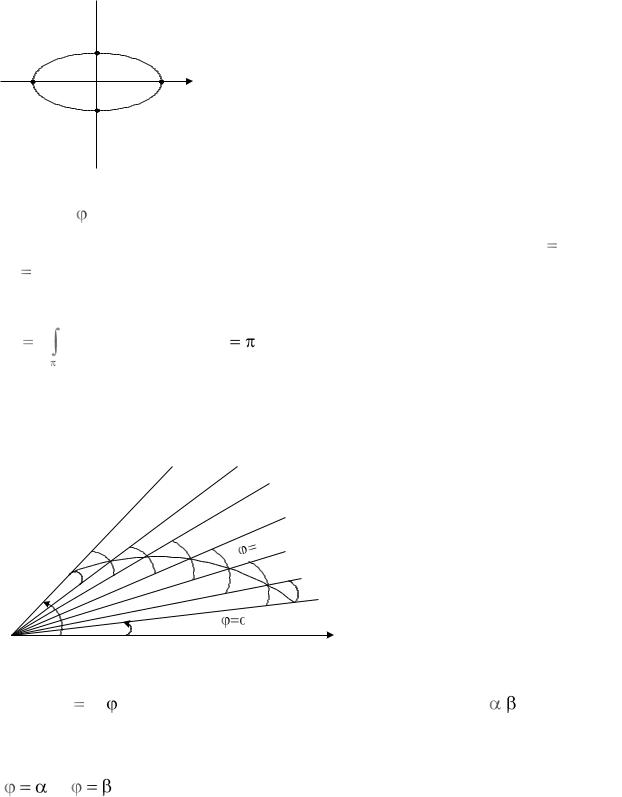
Заўвага 4. Разгледзім крывую AB, зададзеную паметрычнымі раўнаннямі

x

t

, y

t .

Няхай раўнанні вызначаюць функцыю y

f x аргумента х, якая непарыўная і

неадмоўная на адрэзку a, b . Вылічым плошчу Р фігуры, якая абмежавана

прамымі x

a , x

b і крывой АВ (Рыс. 1.12).

y

Скарыстаўшы формулу (16), будзем мець:

b

A

B

P

y dx .

a

Здзейснім у гэтым інтэграле падстаноўку

x

t , тады dx

'

t

dt , y

t

. Атры-

маем:

O

a

b x

t2

P

t

'

t

dt .

(20)

Рыс. 1.12

t1

Новыя ліміты інтэгравання знаходзяцца з

раўнанняў: a

t1

, b

t2

, г. зн. t1 , t2 з’яўляюцца значэннямі параметра,

якія адпавядаюць x

a і x

b .

Такім чынам, мы атрымалі формулу (20) для вылічэння плошчы крывалінейнай трапецыі, якая абмежавана крывой, зададзенай параметрычна.

Адзначым, што пры вывадзе гэтай формулы трэба меркаваць, што функцыі t , t 0 , ' t непарыўныя на адрэзку з канцамі t1 і t2 , а таксама, што

y

b

a

O

x

Рыс. 1.13

функцыя t строга манатонная на гэтым адрэзку.

Прыклад 6. Вылічыць плошчу фігуры, якая абмежавана эліпсам x a cos t ,

y	b sin t (рыс. 1.13).
Рашэнне.
	0
P	4 b sin t a cos t ' dt			ab (кв. адз.).
	2

Вылічэнне плошчы крывалінейнага сектара ў палярнай сістэме каардынат

k
k	1

O
	Рыс. 1.14
Няхай r f	— непарыўная і неадмоўная на адрэзку , функцыя. У

палярнай сістэме каардынат графікам гэтай функцыі з’яўляецца некаторая крывая. Разгледзім плоскую фігуру, якая абмежавана гэтай крывой і праменямі , . Гэтую фігуру будзем называць крывалінейным сектарам

(рыс. 1.14).

Тэарэма 6. Крывалінейны сектар з’яўляецца квадравальнай фігурай. Яго плошчу Р можна вылічыць пры дапамозе наступнай формулы:

P	1		f 2	d	,
	2
г. зн.
P	1		r 2d .					(21)
	2
Доказ. Разбіваем адрэзак ,							на n частак (неабавязкова роўных) пунктамі
	0		1 ...		k 1	k ...	n	.
Няхай			k	k	k 1 (k = 1, 2, … , n).

Пунктам разглядаемай разбіўкі ў палярнай сістэме каардынат будуць адпавядаць наступныя прамені:

, 1, 2, ... , k 1, k, ... , .

Дадзеныя прамені разбіваюць крывалінейны сектар на n частковых крывалінейных сектараў. Зафіксуем увагу на k-тым частковым сектары. Ён абмежаваны праменямі k 1 і k .

Для разглядаемага частковага крывалінейнага сектара пабудуем два кругавыя сектары, якія таксама абмежаваны разглядаемымі праменямі, і радыусы якіх

роўныя

mk

і

Mk , дзе mk — найменшае значэнне непарыўнай на адрэзку

k

1,

k

функцыі r

f

, а Mk

— найбольшае значэнне функцыі r f

на

гэтым адрэзку.

Плошчы пабудаваных кругавых сектараў адпаведна роўныя:

1

m

2

1

f

2

'

k

k

k

2

k

2

і

1

M

2

1

f

2

"

,

2

k

k

2

k

k

дзе

k ' ,

k "

— пункты адрэзка

k 1,

k , у якіх дадзеная функцыя дасягае

адпаведна свайго найменшага і найбольшага значэнняў.

Разгледзім цяпер наступныя сумы:

Q

n

1

m

2

n

1

f

2

'

(22)

k

k

k

1 2

k

1 2

k

k

і

R

n

1

Mk

2

n

1

f

2

"

k .

(23)

k

k

1 2

1 2

k

k

Сума Q — гэта плошча фігуры, якая змяшчаецца ў разглядаемым крывалінейным сектары; сума R — плошча фігуры, якая змяшчае крывалінейны сектар.

Разгледзім якую-небудзь асноўную паслядоўнасць разбівак адрэзка , і

адпаведныя ёй паслядоўнасці сум (22) і (23);

Q1, Q2,	... , Qn, ... ,	(24)
R1, R2,	... , Rn, ... .	(25)

Дадзеныя паслядоўнасці з’яўляюцца паслядоўнасцямі значэнняў інтэгральнай

сумы для функцыі	1		f	2	.
	2

Паколькі функцыя непарыўная на адрэзку , , то яна будзе інтэгравальнай на гэтым адрэзку. Значыць, паслядоўнасці (24) і (25) маюць агульным лімітам

	1	f	2	d :
2
lim Q				lim R		1	f	2	d .
					k
k			k	k		2

Такім чынам, мы пабудавалі дзве паслядоўнасці квадравальных фігур, якія адпаведна змяшчаюцца ў крывалінейным сектары і змяшчаюць крывалінейны

	сектар, плошчы якіх маюць агульным лімітам інтэграл	1	f 2	d .
		2

Калі скарыстаць тэарэму 4, то атрымаем, што крывалінейны сектар з’яўляецца

	квадравальнай фігурай, а яго плошча Р роўная				1	f 2	d :
					2
	P	1	f 2	d .
		2

Тэарэму даказалі цалкам.

O

x

Рыс. 1.15

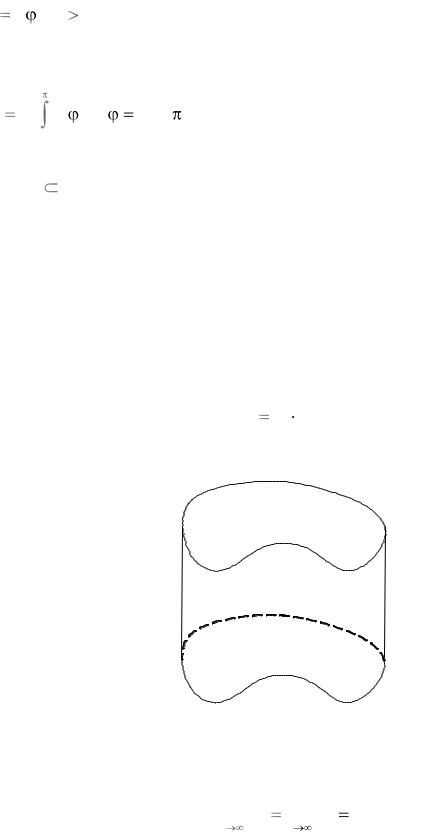
Прыклад 7.	Вылічыць плошчу фігуры, якую абмяжоўвае спіраль Архімеда
r a a	0 і палярная вось (рыс. 1.15).

Рашэнне. Скарыстаўшы формулу (21), атрымаем:

P	1 2		a	2	d	4	a	2	3	(кв.адз.).
	2 0					3

Аналагічна паняццю квадравальнасці ўводзіцца паняцце кубавальнасці цела T R3 .

Лекцыя 2

Вылічэнне аб`ёмаў цел па вядомых плошчах папярочных сечываў. Аб`ём цела вярчэння. Прынцып Кавальеры.

Вылічэнне аб’ёмаў некаторых цел

Тэарэма 2.1. Калі асновай прамога цыліндра з’яўляецца квадравальная фігура P (рыс. 2.1), то гэты цыліндр будзе кубавальным целам, і яго аб’ём вылічваецца па формуле V P H , дзе P — плошча фігуры P , Н — вышыня цыліндра.

H

(P)

Рыс. 2.1
Доказ. Разгледзім многавугольнікі An	і Bn	, якія адпаведна змяшчаюцца ў
фігуры P і змяшчаюць фігуру P , плошчы якіх маюць агульны ліміт, роўны P:
lim An	lim Bn	P .
n	n
На гэтых многавугольніках пабудуем прызмы		Xn і Yn з вышынёй Н.

Прызмы адпаведна змяшчаюцца ў целе V і змяшчаюць гэтае цела. Іх аб’ёмы адпаведна роўныя

роўны V

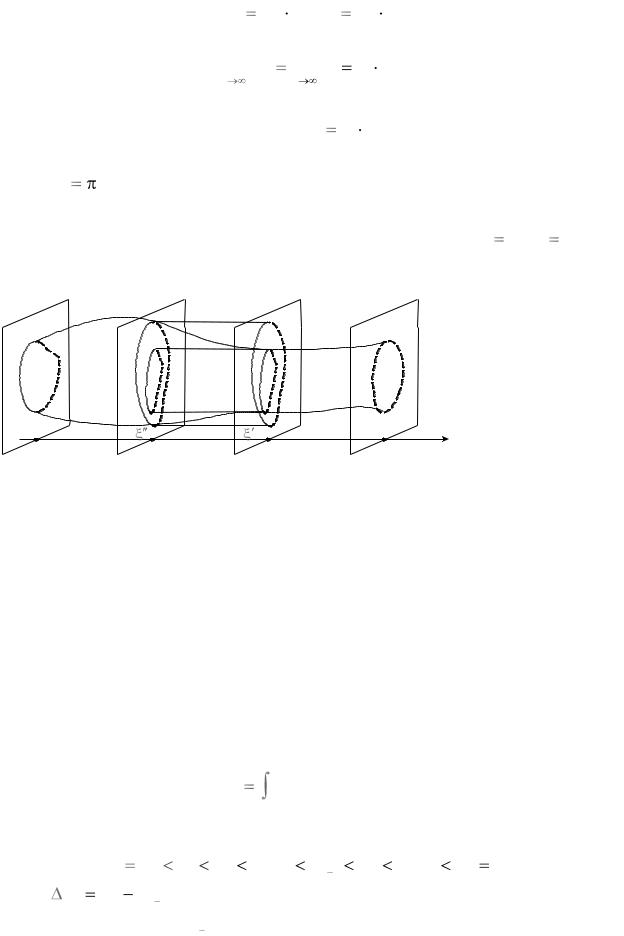
Xn An H , Yn		Bn H
і маюць агульны ліміт:
lim Xn	limYn	P H .
n	n

Калі скарыстаем тэарэму 3, то атрымаем, што дадзены цыліндр з’яўляецца кубавальным целам, а яго аб’ём роўны V P H .

Вынік. Прамы кругавы цыліндр з’яўляецца кубавальным целам, а яго аб’ём r 2H , дзе r — радыус асновы, Н — вышыня цыліндра.

Разгледзім цела V , якое размяшчаецца паміж пласкасцямі x a , x b

(рыс. 1.17).

	k	k
a x0	xk 1	xk	b xn	x

Рыс. 2.2

Будзем перасякаць яго пласкасцямі, перпендыкулярнымі восі Ох. Мяркуем, што ўсе сечывы ўяўляюць сабой квадравальныя фігуры, і што P x — плошча сечыва, якое адпавядае абсцысе х, уяўляе сабой непарыўную на адрэзку a, b

функцыю.

Мяркуем, што, калі любую пару сечываў спраектаваць на плоскасць, перпендыкулярную восі Ох, то праекцыя аднаго з сечываў будзе змяшчацца ў праекцыі другога.

Тэарэма 2.2. Разглядаемае цела V з’яўляецца кубавальным, а яго аб’ём V

можна знайсці па наступнай формуле:

		b
	V	P x dx .		(2)
		a
Доказ. Адрэзак a, b	разбіваем на n частак пунктамі
a x0	x1 x2	xk 1 xk	xn	b .
Няхай xk xk xk	1 , (k = 1, 2, … , n).

Праз пункты x0 , x1, … , xk 1 , xk , … , xn	праводзім плоскасці, перпендыкулярныя
восі Ох. Плоскасці разбіваюць цела V	на n элементарных цел.

Зафіксуем нашу ўвагу на k-м элементарным целе. Яно змяшчаецца паміж

пласкасцямі x xk 1	і x	xk .
Паколькі функцыя P	x	непарыўная на адрэзку			xk 1, xk , то згодна з другой
тэарэмай Вейерштраса яна дасягае свайго найменшага значэння mk						у
некаторым пункце	k ' , а таксама свайго найбольшага значэння Mk					у
некаторым пункце	k " адрэзка		xk 1,	xk :
		mk	P k ' , Mk P		k " .
Пабудуем прамы цыліндр з вышынёй				xk і плошчай асновы mk . Цыліндр

змяшчаецца ў k-м элементарным целе. Аб’ём цыліндра роўны mk xk (тэарэма

5).

Пабудуем таксама прамы цыліндр з вышынёй				xk і плошчай асновы Mk .
Цыліндр змяшчае k-тае элементарнае цела. Аб’ём гэтага цыліндра роўны
Mk xk .
Разгледзім наступныя сумы:
n		n
U	mk xk		P	k ' xk ,
k	1	k	1
n		n
Z	Mk xk		P	k " xk .
k	1	k	1
Сума U ёсць аб’ём цела, якое змяшчаецца ў целе V . Сума Z — аб’ём цела,

якое змяшчае цела V .
Разгледзім якую-небудзь асноўную паслядоўнасць разбівак адрэзка a, b	і
адпаведныя ёй паслядоўнасці значэнняў сум U і Z:
U1, U2, , Uk , ... ,	(3)
Z1, Z2, , Zk , ... .	(4)

Адзначым, што паслядоўнасці (3) і (4) з’яўляюцца паслядоўнасцямі значэнняў інтэгральнай сумы для функцыі P x .

Паколькі функцыя P x непарыўная на адрэзку a, b , то яна і інтэгравальная

на гэтым адрэзку. Таму паслядоўнасці (3) і (4) маюць агульным лімітам

b

P x dx .

a