Матан. М.В.Ишханян

′

= 5

( f (x))

3

+15x (

f (x))

2

′

2x + 2 f (x) f (x)

f (x)

f ′(x) =

2x − 5( f (x))3

15x

( f (x))2

− 2 f (x)

Отсюда находим, что y′

=

2x − 5 y3

.

15xy

2 − 2 y

Найдём y ′′ . Имеем, что

′′

′

′

2x − 5 f 3 (x)

′

y

=

2

=

= ( f (x))

15xf

(x) − 2 f (x)

= (2 −15 f 2 (x) f ′(x))(15xf 2 (x) − 2 f (x)) −

(

2 (x) − 2 f (x)

)

2

15xf

− (2x − 5 f 3 (x))(15( f (x))2 + 2xf (x) f ′(x) − 2 f ′(x)) =

(

)

15xf 2 (x) − 2 f (x)

2

=

(20 f 3

(x) − 75xf 4 (x) − 60x2 f (x) + 4x) f ′(x) − 4 f (x) + 75 f 5 (x)

(

)

2

15xf 2 (x) − 2 f (x)

Подставив в последнем равенстве значение f ′( x) , окончательно получаем

f ′′(x) =		1500xf 6 (x) −120x3 +150x2 f									3 (x) − 250 f 5 (x)						,
					(		(x) − 2	)	3
										f	2 (x)
					15xf 2
Итак, y′ =	2x − 5 y3				, y′′ =	1500xy6 −120x3 +150x2 y3 − 250 y5												.
15xy		2		− 2 y			(				2	− 2	)	3		2
							15xy								y

Задачи

Найти производные неявно заданных функций:

156.x2 y4 +10 = 3x4 y3 + x5 − 5

157.x3 + x2 y − 4 = 2x2 y2 − 6x +1

158.exy = ln ( y2 + x2 )

120

159.arcsin y = x2 y3 − 7yx2

Задачи для самостоятельного решения

										Задание 26
	Найти производные неявно заданных функций:
	26.1.	arccos2 xy + sin y = 1								26.16. y arctg y − arcsin x = 0
	26.2.	ctg( y + 6) = x5 + 2y2								26.17. x4 − 6x2 y2 + 9y4 +15y2 = 0
	26.3.	ctgy + x2 − y = 9								26.18. x2 sin y + 2x − y +1 = 0
	26.4.	2x + 2y							= 2x+ y	26.19. x + ln y − x2ey = 0
	26.5.		x4 + y4						= ex+ y	26.20. ex sin y − e− y cos x = 0
	26.6.		xtgy = x + y2							26.21. x2 y2 − ctgy + 3 = 0
	26.7.	cos			x		+ 34 y = 0			26.22. arctgy = xy
					y					26.23. cos x + e4 y = 9
	26.8.	cos(y + 5) = 2x + y3								26.24. tg( y −1) = x + y2
	26.9.	arccos x − 4y2 = 5								26.25. x −3y + ey = 5
	26.10. x4 − 3y + 2y = 6									26.26. 2x2 + x = y3
			y	+ e		y			= 0	26.27. ex+ y = xy
	26.11.					x
			x							26.28. sin xy = x2 y
	26.12. x2 + y2 ln x − 4 = 0									26.29. x3 + y2 −3xy = 0

26.13. sin(y − x2 ) −3 = 0

26.30. sin y = x + 3 y

26.14.y2 + 5x = 5x − sin y

26.15.exy − y2 = 0

5.7.Дифференциал функции. Правила вычисления дифференциала

Придадим аргументу x в точке x0 приращение x , тогда функция y = f (x) получит приращение

121

f = f (x0 + x) − f (x0 ) .

Если существует число A , такое, что Df = A×Dx + o(Dx) , то говорят, что f (x) дифференцируемая в точке x0 . Линейная часть A × Dx приращения функции называется дифференциалом функции в точке x0 и обозначается df или dy .

Если x – независимое переменное (т.е. не зависит от других переменных), то полагают dx = x .

Вычисление дифференциала

Правила дифференцировании функций аналогичны правилам нахождения производных. Для функций u, v и f справедливы свойства:

d (u + v) = du + dv;		d (u - v) = du - dv;
d (uv) = udv + vdu;	u			=	udv - vdu		, v ¹ 0;
	d
					v	2
	v

Теорема1. Функция f (x) дифференцируема в точке x0 в том и только в том случае, если f (x) имеет производную в этой точке. При этом df = f ′(x0 )dx .

Пример 22 Найти дифференциал функции f = x3

Решение Дифференциал df функции f (x) находится по формуле df = f ′(x)dx , поэтому

df = (x3 )′ dx = 3x2 dx .

Пример 23 Найти дифференциал функции f = 5cos 3x в точке

x0 = π . 2

Решение По правилу нахождения дифференциала функции в точке, имеем

122

	df = f	π
		¢	dx .
		2
		π			3π
Находим,	f ¢(x) = -15sin 3x f ¢			= -15sin					=15 .
		2					2
Следовательно, дифференциал df			функции		f		= 5cos 3x в точке

x0 = π равен 15dx : 2

df = 15dx .

Пример 24 Найти дифференциал функции f = x sin2 x3 .

Решение

df = f ¢dx = (x sin2 x3 )¢ dx =

=(sin2 x3 + x × 2sin x3 cos x3 ×3x2 )dx =

=(sin2 x3 + 3x3 sin2 2x3 )dx

Если в равенстве Df = A × Dx + o(Dx) отбросить бесконечно малую величину o(Dx) , то получим приближённое равенство Df » df , которое применяется для нахождения приближённого значения функции.

Пример 25 Заменяя приращение функции дифференциалом,

найдите приближенно значение			x, если g(-5) = -3, g(x) = -2,96 и
g′(-5) = 2.
Решение По	определению		приращение функции g(x):
g = g(x) − g(x0 ) .		Заменим приращение функции дифферен-
циалом, т.е. будем считать, что Dg » dg .
Тогда, dg = g(x) - g(x0 ) .
Дифференциал	dg	функции	g(x) находится по формуле

dg = g′(x)dx , поэтому

g¢( x0 )dx = g(x) - g(x0 ) . 123

Учитывая, что dx = x = x − x0 , получаем

g¢( x0 ) ×( x - x0 ) = g(x) - g(x0 ) 2 ×( x - (-5)) = -2,96 - (-3)

Т.е.

2 ×( x + 5) = 0,02 Û 2x +10 = 0, 02

Û 2x = -9,88 Û x = -4,98

Пример 26 Найти приближённое значение

15, 75 .

f (x) =

.

Положим x0 =16 ,

Решение Рассмотрим функцию

x

тогда x = 15, 75 −16 = −0.25 .

, где f ( x0 ) =

Имеем, f (x0 + Dx) » f (x0 ) + df

= 4 ,

16

df = f ¢( x0 ) dx , dx = x = −1 / 4 ,

f ′( x) = (

)′ = 1 / (2

) , f ′( x0 ) = 1 / (2

) = 1 / 8 .

x

x

16

1

1

Таким образом, df =

-

= -1 / 32 .

8

4

Окончательно находим

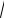15,75 » 4 -1 / 32 =127 / 32 = 3,96875 » 3,97 .

5.8. Дифференциалы высших порядков. Формула Тейлора

Дифференциалом второго порядка d 2 f функции y = f (x) называется дифференциал от дифференциала df , где df рассматривается как функция от x : d 2 f = d (df ) .

Дифференциалом третьего порядка d3f называется диффе-

ренциал от второго дифференциала: d 3 f = d (d 2 f ) и т.д.

Если	переменная	x	является	независимой,		то
d 2 x = d 3 x = ... = d n x = ... = 0 .			В	этом	случае
			124

d 2 f	= f ′′ ( x )(dx )2 ,		d 3 f = f ′′′ ( x )(dx )3 ,...,
d n f = f (n) ( x )(dx )n ,…
Для краткости вместо(dx )n принято			писать	dxn , т.е.
d n f = f (n) ( x)dxn .
Пример 27	Найти	дифференциал	d 3 y	функции
y = x4 − 3x2 + 4 .
Решение Последовательно дифференцируя, получаем
y′(x) = 4x3 − 6x ,		y′′(x) = 12x2 − 6 , y′′′(x) = 24x .
Следовательно, d 3 y = y′′′(x)dx3 = 24xdx3 .

Если функция y = f (x) определена в некоторой окрестности точки x0 и в этой окрестности имеет производные до (n +1) -го

порядка включительно (т.е.

дифференцируема

(n +1) раз), то

справедлива формула Тейлора

f ′′ ( x

)

f ( x ) = f ( x

) +

f ′( x

)

( x − x

) +

( x − x

)

2

+ +

0

0

0

1!

0

2!

0

+

f

(n) ( x

)

( x − x

)

n

+ R

0

(x) ,

n!

0

n+1

где Rn+1 (x) – остаточный член, являющийся бесконечно малой величиной при x → x0 .

Остаточный член обычно записывают в виде

Rn+1 (x) = o (( x − x0 )n ) (в форме Пеано)

	или в виде	f (n+1) (c)
	R ( x) =		( x − x )n+1	(в форме Лагранжа),
		(n +1)!
	n+1		0
			125

где c – некоторое число между x0 и x .

Формула Тейлора допускает и другую запись через дифференциалы

f =	df	+	d 2 f	+	d 3 f	+ +	d n f	+ R	( x )
1!		2!		3!			n!	n+1

.

Формулу Тейлора применяют для приближенных вычислений.

Пример 28 Функцию f (x) = esin x в окрестности точки x = 0

приближенно замените многочленом третьей степени. Решение Положив в формуле Тейлора с остаточным членом в

форме Пеано x0 = 0 , получим

f (x) = f (0) +

f ¢(0)

x +

f ¢¢(0)

x2 +

f ¢¢¢(0)

x3 + o(x3 ),

1!

3!

2!

Последовательно дифференцируя

f (x) , получаем

f ¢(x) = (esin x )¢ = cos x × esin x f ¢(0) = cos 0 × esin 0 =1;

f ¢¢(x) = (cos xesin x )¢ = -sin x × esin x + cos2 x ×esin x

f ¢¢(0) = 0 + cos2 0 ×esin 0 =1;

f ¢¢¢(x) = ((-sin x + cos2 x)esin x )¢ =

+ (-sin x + cos2 x)cos x ×esin x

= (-cos x - 2cos x sin x) × esin x

f ¢¢¢(0) = (-1 - 0) ×1 + (-0 +1) ×1×1 = 0

Учитывая, что f (0) = 1 , имеем

f (x) =1 +

1

x +

1

x2 +

0

x3 + R4 ( x) =1 + x +

x2

+ o (x3 )

1!

2!

3!

2

Пример 29 С помощью формулы Тейлора найти приближённое значение sin 1 с точностью до 0,001.

126

Решение Введём в рассмотрение функцию f (x) = sin(x) . Поло-

жив x0 = 0 , получим			f ′′(0)		f ′′′(0)			(n) (0)		f (n+1) (c)
f (1) = f (0) +	f ′(0)	+		+		+ +	f		+
											,
	1!		2!		3!			n!
										(n +1)!

,

где 0 < c < 1 (формула Тейлора с остаточным членом в форме Лагранжа).

Имеем

f (0) = sin 0 = 0 , f ′(0) = cos 0 = 1 , f ′′(0) = −sin 0 = 0 ,

f ′′′(0) = − cos 0 = −1,								f IV (0) = sin 0 = 0 , …,
R		=		f (n+1) (c)		≤		1		.
				(n + 1)!			(n + 1)!
n+1

Для вычисления требуемого значения нужно взять n таким,

чтобы		Rn+1		< 0, 001	, или	1		<		1	; (n + 1)! > 1000 .
						(n + 1)!			1000

Это неравенство достигается при n = 6 , так как 6! = 720 < 1000 ,

а 7! = 5040 > 1000 . Поэтому

sin1 ≈ 1 −	1	+		1	=	101	≈ 0,8417 ≈ 0,842
			120
6					120

Пример 30 Напишите разложение многочлена четвертой степе-

ни P(x)	по степеням x −10 , используя формулу Тейлора. Най-
дите	P′′(10) , если P(10) = 4 , P′(10) = 1, P′′′(10) = 18 ,

P( 4) (10) = 48 и P(11) = 11 .

Решение Положив в формуле Тейлора с остаточным членом в

форме Лагранжа x0 = 10 , получим

P′′(0)

P(x) = P (10) +

P′(0)

( x −10) +

( x −10)

2

+

1!

2!

′′′

(4)

(5)

+

P (0)

( x −10)3 +

P

(0)

( x −10)4 +

P

(c)

,

5!

3!

4!

где 0 < c < 1 .

127

Учитывая, что по условию задачи степень многочлена равна че-

тырем, а P(10) = 4 ,

P′(10) = 1,

P′′′(10) = 18 ,

P( 4) (10) = 48 , имеем

P(x) = 4 +

1

( x

−10) +

P′′(0)

( x

−10)

2

+

18

( x −10)

3

+

48

( x −10)

4

=

1!

2!

3!

4!

= 4 + ( x −10) +

P

′′

(0)

( x −10)2 +

18

( x −10)3 +

48

( x −10)4 =

2

24

′′

(0)

6

= x − 6 +

P

( x −10)2 + 3( x −10)3 + 2( x −10)4

2

Так же нам известно, что P(11) = 11 . С другой стороны, по фор-

муле Тейлора

P′′(0)

P(11) = 11 − 6 +

(11 −10)

2

+ 3(11 −

10)

3

+ 2(11 −10)

4

2

P′′(

0)

P(11) =

+ 11 − 6

+ 3 + 2

2

0)

P(11) =

P′′(

+ 10

2

P′′(10)

P′′(10)

Получаем, что

+ 10 = 11

= 1 P′′(10) = 2 .

2

2

Задачи

Найти дифференциал функции:

y = ln (sin

)

160.

y = x5

164.

x

161.y = tgx

						1
162.	y = sin3 2x				165.	y = e−
										cos x
163.	y = ln x				166.	y = 2− x2
Найти дифференциал функции в точке x0 :
167.	y = x	−4		= −1
			, x0		169.	y = 1 + x							2			, x0	= −3
	y = x3 − 3x2 + 3x, x0
168.					= 0	y =	1		−		1						= 2
					170.										, x
							x x2								0
					128

				π	173.	y =		+ 1, x0 = 4
171.	y = ln cos x, x0	=					x
				4
	y = e−2 x , x = −		1		174.	y = arctg 4x −1, x0 = 3
172.
	0	2

Найти дифференциал второго порядка:

175.y = ctgx

176.y = cos2 x

177.y = ln (2x − 3)

Найти дифференциал третьего порядка:

178.y = ex cos x

179.y = x ln x

180.Заменяя приращение функции дифференциалом, найдите приближенно значение x, если g(5) = 2, g(x) =

2,04		и g′ (5) = -4.
181.	Заменяя приращение		функции	дифференциалом,
найдите приближенно значение x, если g(-5) = 2, g(x) =
2,04		и g′ (-5) = -4.
182.	Заменяя приращение		функции	дифференциалом,
найдите приближенно значение x, если g(-3) = 5, g(x) =
5,04		и g′ (-3) = -2.
				1
183.	Напишите разложение функции f			(x) =		по степе-
					x − 2

ням x − 1 до члена четвертого порядка включительно.

184.Найдите три члена разложения функции f (x) = 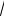x по степеням разности x − 1 .

185.Функцию f (x) = e2x−x2 в окрестности точки x = 0 при-

ближенно замените многочленом третьей степени.

186. Напишите разложение многочлена четвертой степени P(x) по степеням x −11, используя формулу Тейлора. Най-

дите	P′′′(11) , если	P(11) = 5 , P′(11) = 4	′′	= 6 ,
			, P (11)

P(4) (11) = 72 и P(10) = 5 .

129