Курсовая работа по эктродинамике4

Министерство образования и науки РФ

Уфимский Государственный Авиационный Технический Университет

Курсовая работа по дисциплине

«Электромагнитные поля и волны»

Вариант 12.

Выполнил студент гр. МКС-317

Исламов А. И.

Проверил преподаватель:

Филатов П.Е.

Уфа – 2007 г.

Часть 1.

Задание:

1. Рассчитать проводимость системы на единицу длины. Найти ток утечки.

2. Рассчитать и построить графики распределения напряженности электрического поля и потенциала в плоскости KF.

3. Рассчитать и построить вектор плотности тока в точке М.

4. Провести эквипотенциаль с потенциалом, равным 0,25U, где U – приложенное напряжение.

Исходные данные:

Схема 8

R = 2,2 мм = 2,2·10^-3 м;

d = 24 мм = 0,024 м;

h = 26 мм = 0,026 м;

U = 320 В;

σ = 3,5·10^-5 См/м

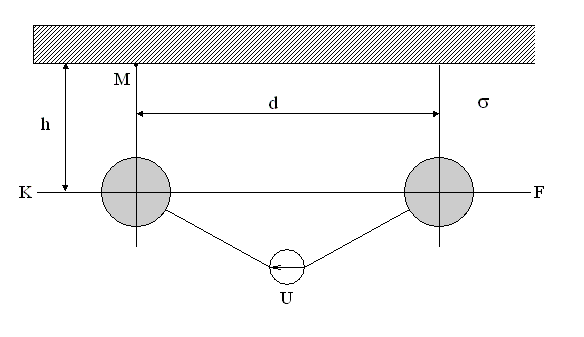
Рис.1. Симметричная пара с радиусом жилы R, расположенная под проводящей плоскостью в среде с проводимостью .

1. Задача о поле двухпроводной линии сводится к задаче о поле двух заряженных осей. Расчет задачи проводим при помощи метода зеркальных изображений. Его суть заключается в следующем. В результате электростатической индукции на проводящей поверхности выступают заряды. Для расчета такой системы кроме заданных заряженных осей вводят ещё дополнительную фиктивную пару осей, линейные плотности зарядов которых будут равными по значению, но противоположные по знаку зарядам в реальной паре.

Рис. 2. Рабочий чертеж системы.

Потенциал в любой точке:

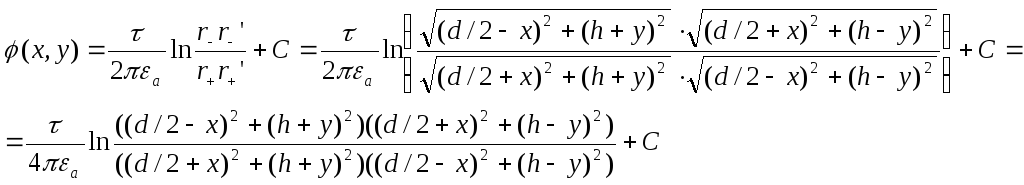
Константу С находим из условия: х=0, y=0, φ=0 (оси - эквипотенциальные поверхности с нулевым потенциалом):

X_a = - d/2 + R = -9,8 мм

X_b = d/2 – R = 9,8 мм

Y_a = Y_b = h = -26

Емкость системы на единицу длины:

Проводимость системы на единицу длины:

Ток утечки:

2. Потенциал в любой точке определяется по формуле:

Так как , то для нахождения и продифференцируем выражение по x и y, получим:

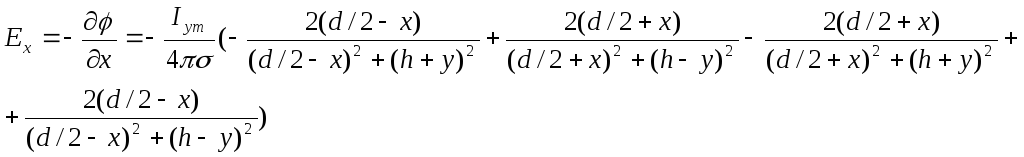
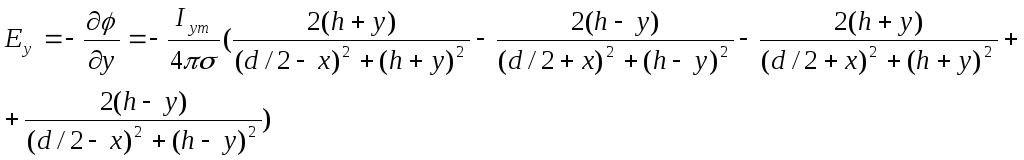
Подставим числовые значения. В плоскости KF потенциал и напряженность электромагнитного поля будут зависеть только от x, т. к. y=const= -26 мм:

Рис. 3. График распределения потенциала в плоскости KF.

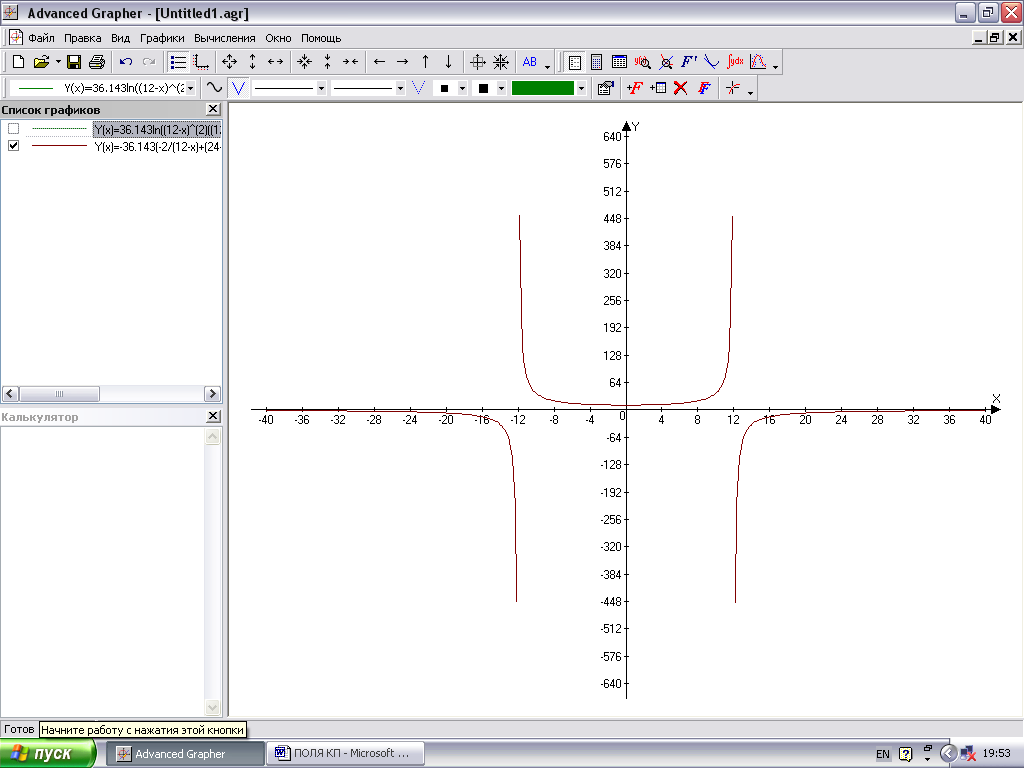
Рис. 4. График распределения напряженности электрического поля в плоскости KF.

3. Точка М имеет координаты x = -12; y = 0.

Напряженность поля в точке М:

Модуль напряженности поля в точке М:

E=E_y=2.558 В/м.

Вектор плотности тока:

Модуль вектора плотности тока:

j = 8.953·10^-5 В/м²

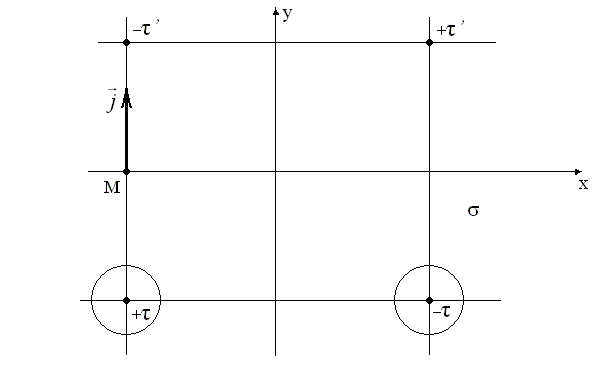
Рис. 5. Вектор плотности тока.

4. φ=0,25U=0,25·320=80 В

Потенциал в любой точке:

График, являющийся решением этого уравнения приведен на рис. 6.

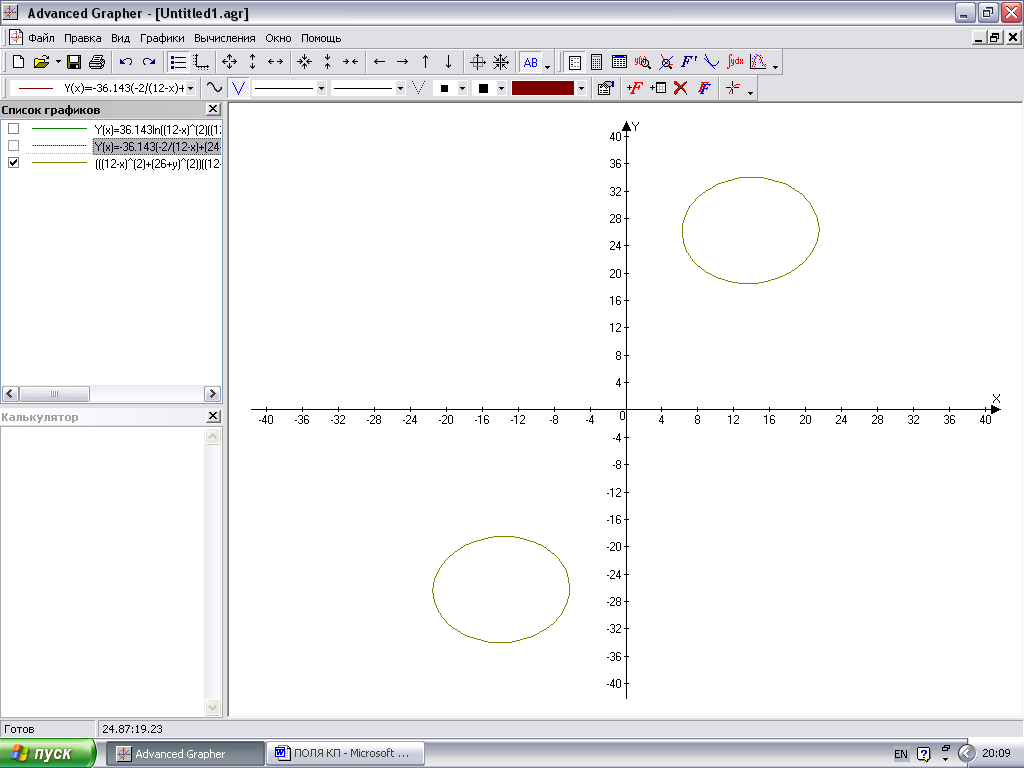
Рис 6. Чертеж эквипотенциали.

Часть 2.

Задание:

По круглому цилиндрическому проводнику протекает синусоидальный ток i=I_m sin ωt, A.

Радиус проводника R, удельная проводимость материала σ, относительная магнитная проницаемость μ.

Определить плотность тока и напряженность магнитного поля внутри проводника. Числовой ответ дать для точек, находящихся на расстоянии от оси провода r=0; r=0,25R; r=0,5R; r=0,75R; r=R при двух частотах: f и nf.

Построить графики зависимостей модулей плотности тока и напряженности магнитного поля от r.

Исходные данные:

Im=3,9 А R=1,7 мм = 1,710^-3м =0,810^7Cм/м =150 f=75 Гц n=8

Амплитудное значение синусоидального тока; Радиус проводника; Удельная проводимость материала; Относительная магнитная проницаемость; Частота; Номер гармоники.

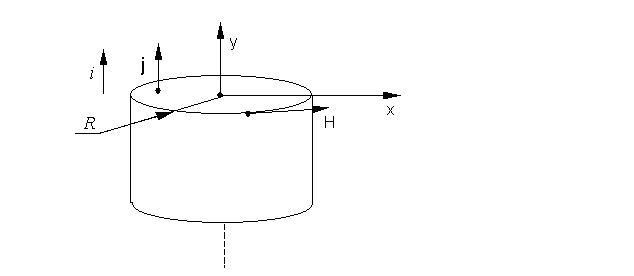
Рис. 7. Чертеж системы.

Электромагнитное поле для неподвижных тел и сред описывается системой уравнеий Максвелла:

(1);

(2);

(3);

(4);

(5);

(6);

(7).

По условию, ток i во времени изменяется по гармоническому закону, значит , связанный с i равенством , изменяется гармонически. Исходя из (7), (5), (1) и (6) заключаем, что изменеия ,, и также носят гармонический характер.

Поэтому все дальнейшие расчеты будем производить в комплексной форме.

Умножим (2) на σ, и в силу (7) и всего выше изложенного (2) примет вид:

(8).

Уравнение (1) с учетом (5) и (7):

(9).

Отношение , значит с большой степенью точностью вторым слагаемым в правой части уравнения (9) можно пренебречь, тогда:

,

или

(10).

От обеих частей уравнения (8) возьмем операцию ротора, получим:

.

Далее, исходя из (10) и соотношения , имеем:

(11).

Возьмем операцию дивергенции от обеих частей (10):

.

Из теории поля известно, что , значит . Тогда (11) примет вид:

(12).

В цилиндрических координатах . от и z не зависит и направлено вдоль оси цилиндра. Получаем:

.

Обозначим . Тогда

или

(13).

В математике известно, что решение уравнения (13) записывается в виде

,

здесь J₀(qr)- функция Бесселя первого рода нулевого порядка, N₀(qr)- функция Бесселя второго рода нулевого порядка.

N₀(qr) при qr=0 обращается в бесконечность. Из физических соображений всюду конечен, поэтому принимаем В=0.

Из (8) определим, учитывая, что , в цилиндлических координатах :

,

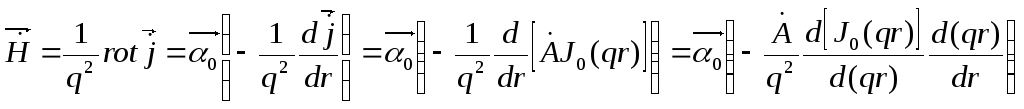здесь - единичный орт оси 0. , - функция Бесселя первого порядка первого рода. Т. е.

(14).

Из закона полного тока определим на поверхности провода (при r=R), приравняем его значению , полученному из соотношения (14) и определим :

,

.

Окончательно получаем:

Для цилиндрического проводника плотность тока определяется по формуле:

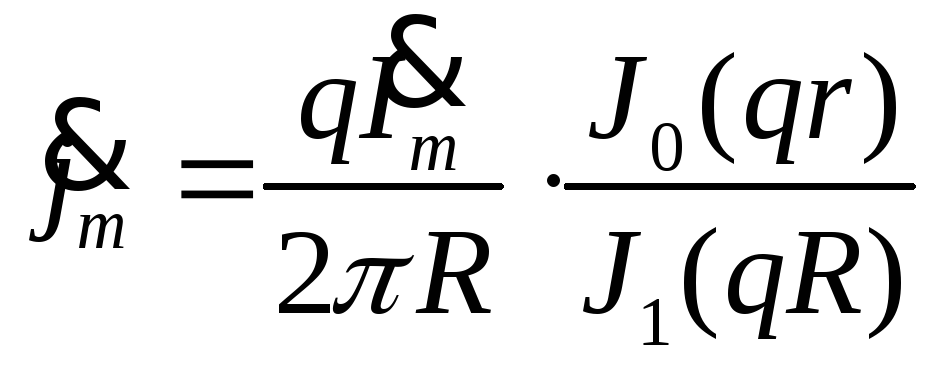, где

Напряжённость магнитного поля равна:

Бесселевы функции J₀(qr) и J₁(qr) от комплексного аргумента тоже являются комплексами и могут быть представлены в показательной форме:

,

где b₀-модуль, а β₀—аргумент функции J₀(qr); b₁-модуль, а β₁—аргумент функции J₁(qr).

Аргументами β₀ и β₁ пренебрегаем и не используем в вычислениях, т.к. графики строятся по значению модуля функции Бесселя. Т.е. запишем это в виде:

Расчеты:

рад/с;

_{а=  0 = 150  4  10}^-7 _{= 188,4  10}^-6 _Гн/м;

- на поверхности проводника.

По графику находим , это значение будет постоянным во всех последующих расчётах для частоты f.

; ;

Результаты расчетов сведены в таблицу 1:

R	0	0,25R	0,5R	0,75R	R
r, м	0	0,000425	0,00085	0,001275	0,0017
	0	0.358	0.7162	1.0743	1.432
	1	1.0056	1.0117	1.035	1.1076
	0	0.1794	0.3587	0.5414	0.73482
jm, А/м^2	413793.69	416110.94	418635.09	428276.48	458317.9
Hm, А/м	0	88.107	176.17	265.89	365.305

Определим плотность тока и напряженность магнитного поля внутри проводника при nf=600 Гц.

рад/с;

_{а=  0 = 150 4  10}^-7 _{= 188,4  10}^-6 _Гн/м;

- на поверхности проводника.

По графику находим , это значение будет во всех последующих расчётах для частоты nf.

Результаты расчетов сведены в таблицу 2:

R	r	0,25R	0,5R	0,75R	R
r, м	0	0,000425	0,00085	0,001275	0,0017
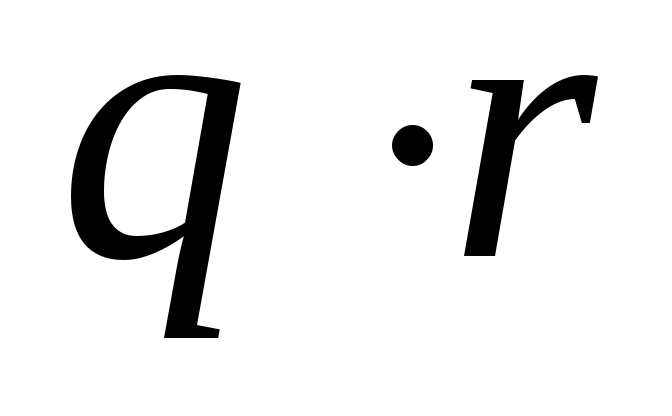
	0	1.013	2.026	3.038	4.051
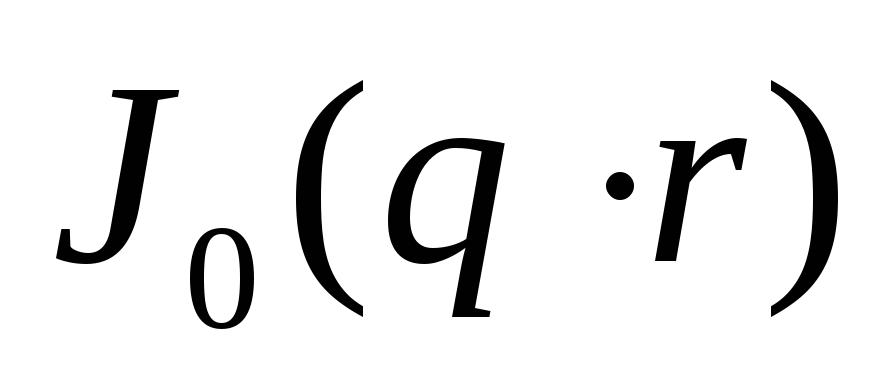
	1	1.018	1.248	2.008	3.584
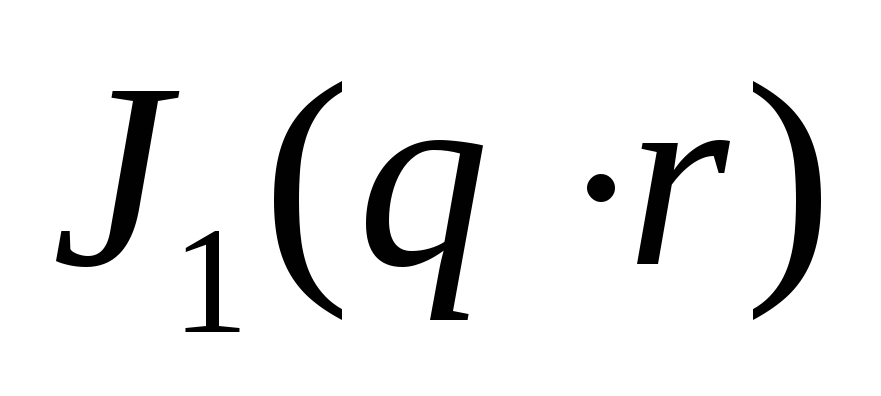
	0	0.508	1.061	1.853	3.31
jm, А/м^2	263007.72	267741.86	328233.63	528119.5	942619.66
Hm, А/м	0	56.065	117.096	204.504	365.305

Рис. 8. График зависимости j_m от расстояния от оси провода.f = 75 Гц,nf = 600 Гц)

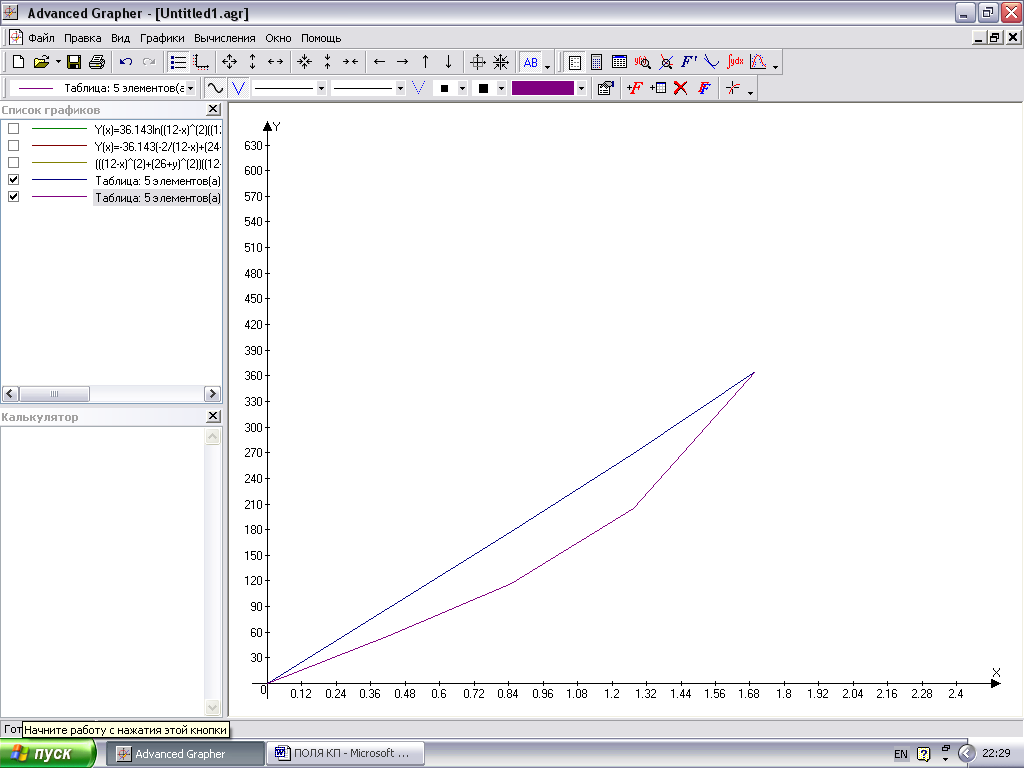
Рис. 10. График зависимости H_m от расстояния от оси провода для частот f=75 Гц и nf=600 Гц.

Часть 3.

Задание:

По отрезку прямолинейного провода длиной 1 проходит переменный ток i = I_msinl0⁸t A. Среда, окружающая провод, - воздух. Считать, что со средней точкой отрезка провода со­вмещено начало отсчета сферической системы координат, ось отсчета угла θ совпадает с положительным направлением тока в проводе, ось отсчета угла α совпадает с положительным направлением оси Х.

Требуется:

1. построить полярную диаграмму зависимости от угла θ модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

2. записать выражения для мгновенных значений векторов напряженности электриче-­ ского и магнитного полей в точках А и В, предварительно выяснив, в какой зоне поля нахо­- дится каждая точка. Радиус R, координаты точек А и В в сферической системе координат приведены в таблице.

Исходные данные:

l = 11 см = 0.11 м Im = 115 А R = 600 м RА = 0,92 м А = 40 ° RВ = 850 м В = 220 °

Длина отрезка прямолинейного провода; Амплитудное значение синусоидального тока; Радиус сферы; Координаты точки А в сферической системе координат; Координаты точки B в сферической системе координат.

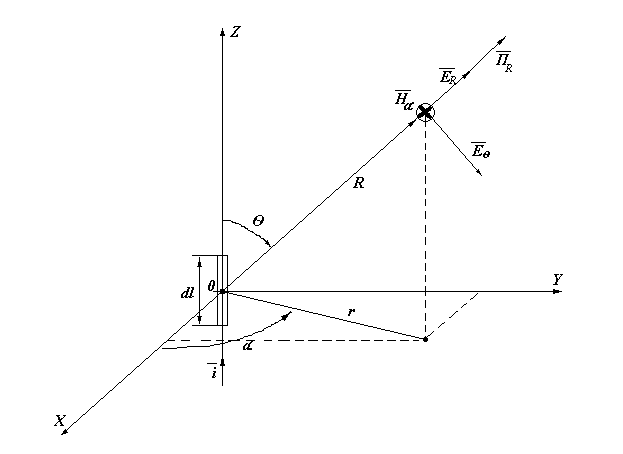
Рис. 10. Чертеж системы.

1. Построим полярную диаграмму зависимости от угла  модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

Ток i = I_msin10⁸t, A → ω=10⁸ ;

Оценим дальность точек находящихся на сфере (Расстояние R).

, значит точки сферы радиуса R лежат в дальней зоне.

Тогда мгновенные значения для E и H

Для воздуха .

Выражение вектора Пойнтинга для дальней зоны:

Модуль вектора Пойнтинга (мгновенное значение):

_{Среднее за период значение:}

По этой функции построим полярную диаграмму зависимости от угла  модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

Рис. 11. Диаграмма направленности.

2. Запишем выражения для мгновенных значений векторов напряженности электрического и магнитного полей в точках А и В, предварительно выяснив, в какой зоне поля находится каждая точка.

Ток i = I_msin10⁸t, A → ω=10⁸;

Оценим дальность точек A и B.

2.1. Точка А (R_А=0,92м).

- значит точка A находится в средней (промежуточной) зоне.

Мгновенные значения напряжённости электрического ( и ) и магнитного () поля вычисляем исходя из формул.

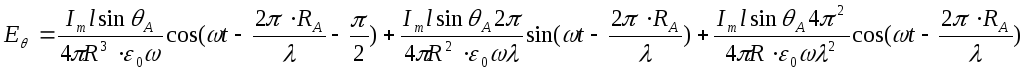E_θ=939.8035sin(10⁸t-107.58°)+288.206sin(10⁸t-17.58°)+88.38cos(10⁸t-17.58°)

E_R=2240.028sin(10⁸t-107.58°)+686.942 sin(10⁸t-17.58°)

H_α=0.7649 sin(10⁸t-17.58°)+0.2346 cos(10⁸t-17.58°)

2.2. Точка B (R_B=850м).

- значит точка В находится в дальней зоне.

Мгновенные значения напряжённости электрического () и магнитного () поля вычисляем исходя из формул: