лекции, учебные пособия / конспект лекций / Lekcii / Лекция 5 (Соснин В

4. Метод ранжирования критерия

1. определяем относительный ранг каждого из критериев: W1>W2>W3>…

2. проводим оптимизацию по самому важному критерию (W1)

3. проводим оптимизацию по критерию W2 с учетом ограничений, наложенных в пункте 2

4. и так далее до последнего критерия

Пример: есть два минимизируемых критерия W1 и W2. Тогда решение обозначается звездочкой для разных соотношений приоритетов критериев.

5. Метод лексикографической оптимизации

(принцип поиска слова в словаре)

1. определяем относительный ранг каждого из критериев: W1>W2>W3>…

2. задаемся двумя альтернативами a’ и a’’, тогда

• при (W1’ > W1’’) имеем a’ > a’’

• при (W1’ = W1’’) и (W2’ > W2’’) имеем a’ > a’’

• при (W1’ = W1’’) и (W2’ = W2’’) и (W3’ > W3’’) имеем a’ > a’’

• и так далее

в итоге получаем, какая из двух альтернатив лучше

6. Метод последовательных уступок

Пусть есть область решений U. Пусть наши критерии максимизирующие.

1. Определяем относительный ранг каждого из критериев: W1>W2>W3>…

2. Проводим оптимизацию только по критерию W1, находя некоторое решение X1= max W2(U).

3. Переводим W1 из ранга критериев в ранг ограничений, давая ему некоторый запас изменения в худшую сторону. Этому будет соответствовать некоторая уступка в значении X1. Эта уступка обозначается ∆1. При этом W1(U) ≥ X1 - ∆1

4. Проводим оптимизацию по W2, в пределах заданной уступки ∆1. Находим новое решение Х2(∆1)=max W2(U).

5. Аналогично Х1 задаем уступку для Х2. При этом W2(U) ≥ X2 - ∆2

6. Проводим оптимизацию по W3, в пределах заданных уступок и ∆2 . Находим новое решение Х3(∆1∆2)=max W3(U).

7. Аналогично Х1 и Х2 задаем уступку для Х3. При этом W3(U) ≥ X3 - ∆3

8. Повторяем для всех критериев

Пример:

Пусть наши критерии максимизирующие. Тогда решение обозначено звездочкой.

7. Метод выработки обобщенного критерия

Пример: стоимость/производительность, производительность/стоимость, …

Принцип абсолютной уступки

«Справедливым является такой компромисс, при котором суммарный абсолютный уровень снижения одного или нескольких критериев не превосходит суммарного абсолютного уровня повышения других критериев».

Пусть есть два решения Е₀(е¹₀, е²₀, …, е^к₀) и Е₁(е¹₁, е²₁, …, е^к₁)

Если ∆_абс > 0, то решение Е1 лучше решения Е0

Если ∆_абс < 0, то решение Е0 лучше решения Е1

Критерий оптимизации:

Пример:

Даны два решения Е0(2,7) и Е1(3,5).

Тогда ∆_абс = (3-2) + (5-7) = -1 < 0 ==> E0 лучше Е1

Принцип относительной уступки

«Справедливым является такой компромисс, при котором суммарный относительный уровень снижения качества одного или нескольких критериев не превосходит суммарный относительный уровень повышения качества по остальным критериям».

Пусть есть два решения Е₀(е¹₀, е²₀, …, е^к₀) и Е₁(е¹₁, е²₁, …, е^к₁)

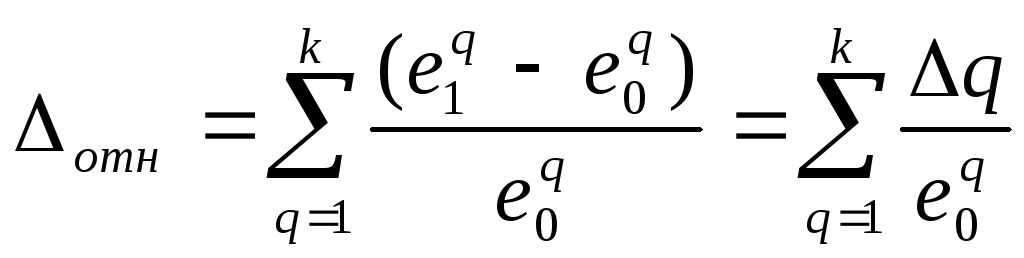
Если ∆_отн > 0, то решение Е1 лучше решения Е0

Если ∆_отн < 0, то решение Е0 лучше решения Е1

Критерий оптимизации:

Пример:

Даны два решения Е0(2,7) и Е1(3,5).

Тогда ∆_отн = (3-2)/2 + (5-7)/7 = 3/14 > 0 ==> E1 лучше Е0

Оба этих метода осуществляют переход от векторного задания критериев к скалярному.

Аддитивный скалярный критерий

1. нормируем все значения критериев, принимая, что все критерии равнозначны:

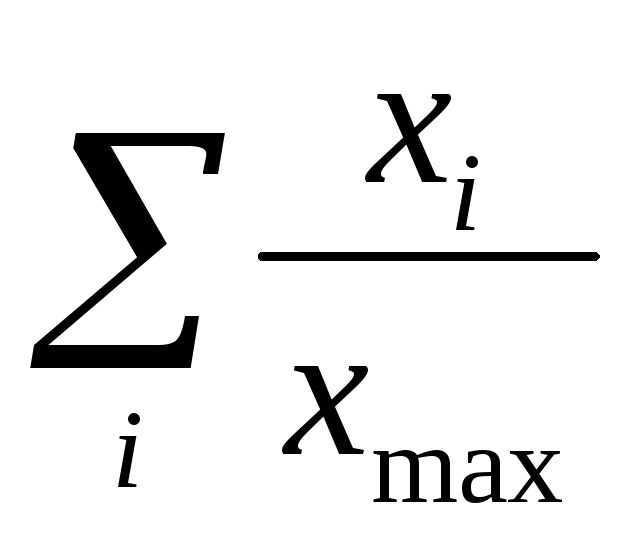
2. вводим ранжирование критериев с помощью параметра α_i -

при этом и

Критерий оптимальности:

Пример:

. D – область компромиссов. Из рисунков очевидно, что данный критерий неприменим в случае невыпуклой области D.

Замечание: если критерий максимизирующий, то он берется со знаком «плюс», иначе – со знаком «минус».

Мультипликативный скалярный критерий

1. вводим критерий

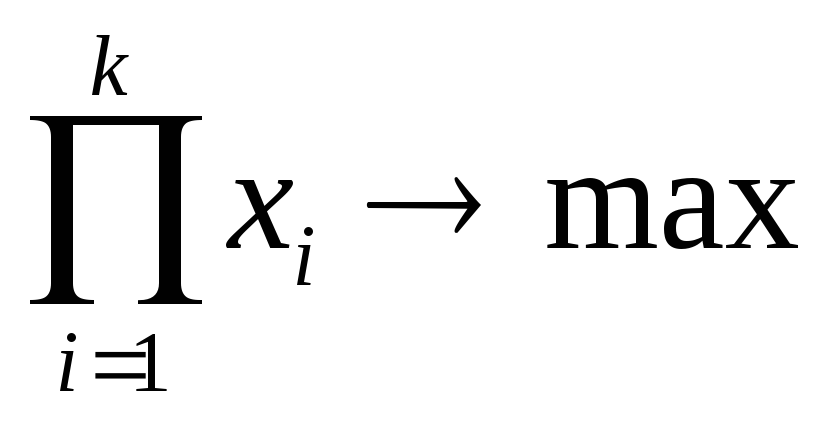
2. добавляем ранжирование

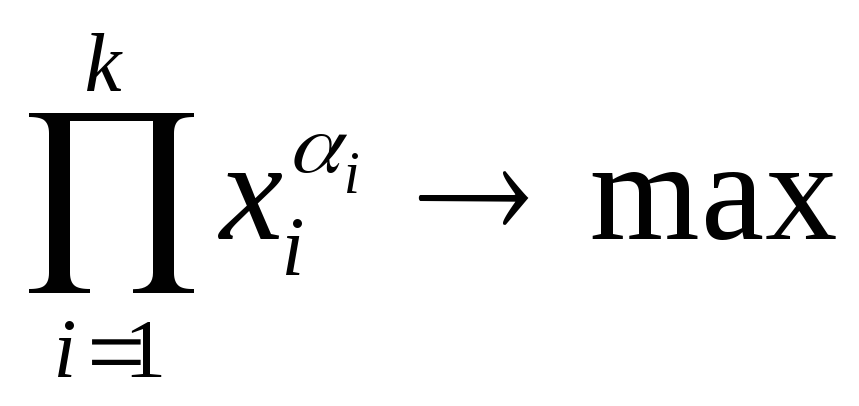
Замечание: если критерий максимизирующий, то он ставится в числитель, иначе – в знаменатель.

Мультипликативный критерий можно свести к аддитивной форме:

Можно учесть оба критерия: мультипликативный и аддитивный.

Варьированием параметра β от 0 до 1 вводится значимость аддитивного и мультипликативного критерия в общей сумме.

Метод отклонения от идеала (целевое программирования)

Из всего множества решений всегда можно выделить идеальное. Тогда критерий качества решения – это его отклонение от идеального.

f_i0 – идеальное значение показателя, тогда

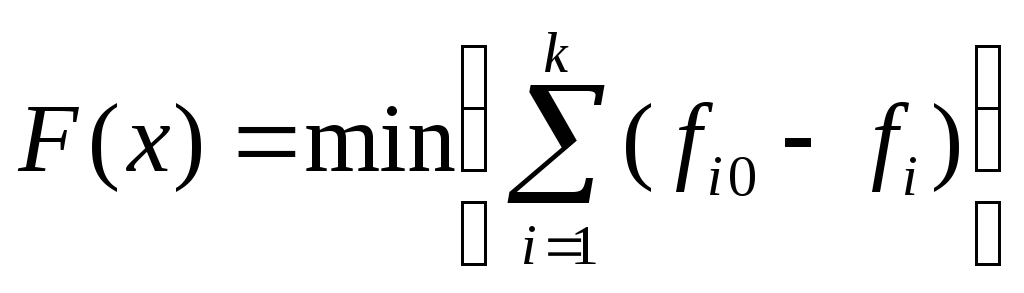- критерий оптимизации

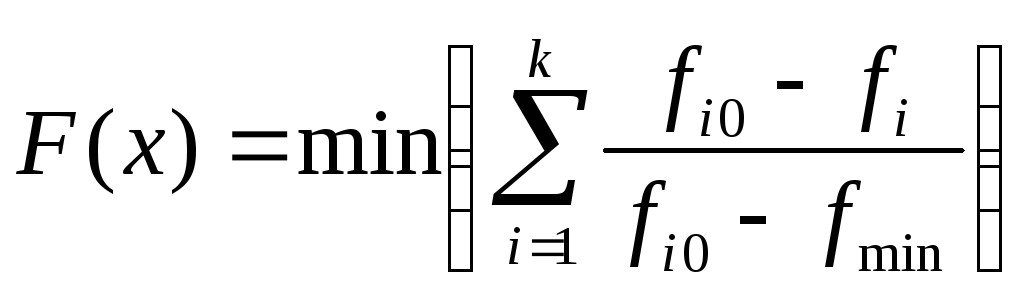- после нормировки

Учет ранга критериев вводится с помощью коэффициентов α_i, вводимых либо как сомножители, либо как показатели степени.

Пример:

Даны альтернативные решения:

f(x1) = (10;10;3), f(x2) = (8;8;10), f(x3) = (0;0;0)

1 способ. После нормировки получим:

f(x1): (1;1;0,3) ∑ = 2,3

f(x2): (0,8;0,8;1) ∑ = 2,6

f(x3): (0;0;0) ∑ = 0

Очевидно, что лучшее решение номер два.

2 способ. Решение 3 заведомо хуже первого и второго, поэтому отбросим его. После этого нормируем оставшиеся два решения:

f(x1): (1;1;0) ∑ = 2

f(x2): (0;0;1) ∑ = 1

Видим, что теперь лучше решение 2. Получаем противоречие с первым способом решения.