лекции, учебные пособия / конспект лекций / Lekcii / Лекция 3 (Латманизова М

Лекция 3.

Многокритериальная оптимизация.

Функция полезности.

Первым ее ввел Леонтьев (США).

Функция полезности – это числовая функция , определяемая на множестве альтернатив и такая, что выполняется следующее условие:

Если одна альтернатива лучше другой, то ф-ция полезности от этой альтернативы должна быть больше, чем от другой альтернативы, т.е. она дает возможность численно сопоставить некоторые альтернативы:

Если Ai и Aj эквивалентны, то их ф-ции равны

Ai ~ Aj F(Ai) = F(Aj) для любого Aj, принадлежащего А

Ai > Aj F(Ai) > F(Aj) (не сравнимы = эквивалентны)

Для любого Ai и Aj, принадлежащих А таких, что:

Ai > Aj Aj > Ai Aj ~ Ai

На множестве альтернатив должно выполняться бинарное отношение транзитивности.

Вид функции полезности.

Рассмотрим на некоторых примерах, как выразить полезность.

1. Разные частоты передачи Ethernet – как они отражаются на полезности.

f

2. Разработка кластерной RAID – системы.

Зависимость полезности от частоты обмена:

3. Освещенность на рабочем месте:

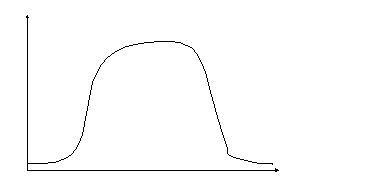
интенсивность

Для аппроксимации используется такое понятие, как кривая безразличия.

Кривая безразличия - если х1 ~ х2 , то они лежат на одной кривой безразличия. Если же х3 более предпочтительно, чем х1, то х3 лежит на кривой, соответствующей более предпочтительной альтернативы.

Область решения

Хс - решение

Хс принадлежит области решений такой, что: для любого Х принадлежащего области решений Хс > Х.

2 функции полезности V1 и V2 (V1 ~ V2) стратегически эквивалентны, если они имеют одни и те же кривые безразличия. Если нас есть любая монотонно возрастающая функция Т, то выполняется следующая закономерность:

T(V1)=~V2

T – преобразование, выполняемое над V1

V1=∑]Ki*Xi ~ √∑]Ki*Xi ~ log∑Ki*Xi

Задачи векторной (многокритериальной) оптимизации.

Возникает:

• Если много целей

• Если много объектов, каждый из которых оценивается по своим параметрам (например, построение корпоративной сети, каждый этап построения которой оценивается по своим параметрам)

• Если объект функционирует в различных условиях, в каждых из которых свои требования (например, Notebook, который работает и от сети, и на батарее)

• Если система многофункциональна

• Если система циклически выполняет различные задачи

Трудности:

• Противоречия между критериями

• Выбор принципа оптимальности

• Учет приоритетов различных критериев

• Различные критерии измеряются в различных единицах, которые трудно согласовать

Чтобы согласовать различные единицы измерения, надо произвести нормирование:

V – значение параметра

Сq[в степени h] – нормированное идеальное значение параметра

Т.е. берется некоторое значение и делится на идеальное значение. Это получается безразмерная величина.

Три варианта нормировки:

1. В качестве нормирующих используется значение заранее заданное (опрос, экспертная оценка) (минус этого метода – полный субъективизм)

2. В качестве нормирующего значения выбирается максимальное значение показателя:

Е1/ max E или E1/(max E – min E)

А вообще каждый как хочет, так и нормирует!

Сопоставление по важности: КОЭФФИЦИЕНТ ЗАМЕЩЕНИЯ.

Есть 2 параметра х и у. Если у увеличить на ∆, то на сколько можно уменьшить х, чтобы это компенсировать?

λ – предельный коэф. замещения (характеризует готовность уступки по одному параметру ради выигрыша в другом).

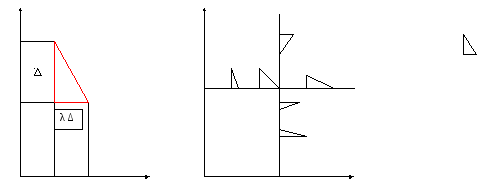
Эффективность решения:

A' x=(x’1, x’2, …x’m) x’≥x”,если для любого i (x'i≥x”i) Λ (существует i x’i>x”i)

A” x=(x”1, x”2, …x”m) |

Доминирование по Парето

Если для некоторой точки у0 принадлежит У не существует более предпочтительного решения по Парето, то это решение называется эффективным или Парето - оптимальным решением.

Если для любого i (x'i ≥x”i), то такое решение называют слабоэффективным решением многокритериальной задачи или решением оптимальности по Слейтеру. Любой исход не может быть улучшен сразу по всем критериям.

Примеры оптимальной точки:

5

4

при переходе 5-1, 1-2, 3-4, 4-5 улучшается только один критерий. При 2-3 эти решения не доминируют по Парето, т.к. один параметр лучше, а др. хуже.

{1,2,3,4} - слабоэффективное решение, {2,3} – эффективное решение

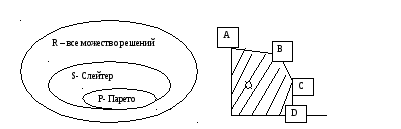
ABCD – S – решение

BC – Р - решение

5