лекции, учебные пособия / конспект лекций / Lekcii / Лекция 12 (Латманизова М

Лекция 12.ТПР, Латманизова М.

Рассмотрим пример на примере лабораторной работы 2: разбиение на сегменты. Мы можем только прогнозировать загрузку, и поэтому эта задача - типичная задача принятия решений в условиях неопределенности.

Управл. запросы – интенсивность запросов четко известна и жестко определена (принятие решений в условиях определенности).Еще одна особенность принятия решения в условиях неопределенности: мы не противопоставляем себя природе (не то, что нам кто-то хочет навредить).

Рассмотрим ситуацию, когда нам противостоит некоторый противник (теория игр и экономическая теория (ситуация: когда я выигрываю, ты проигрываешь)).

Кратко пройдем теорию игр. В теории игр есть динамическое программирование (поэтапное принятие решений).

Теория ИГР.

Это математическая теория конфликтных ситуаций. Выделяются 2 класса игр. В основном, исследуются игры с нулевой суммой (если мы выигрываем некоторую сумму, то кто-то непременно проигрывает эту же сумму, так что в результате сумма выигрыша и проигрыша равна 0. Другими словами, если где-то что-то убыло, то в другом месте прибыло ).

Рассмотрим ситуацию «перекресток»:две машины едут навстречу друг другу (вы и кто-то).

Если вы оба снизите скорость, никто из вас ничего не проиграет (оба живы останетесь).

Если вы затормозите, а кто-то нет, то вы проиграете.

Если вы не снизите скорость, а кто-то снизит, то он проиграет.

Если оба не снизите скорость, то оба проиграете (БУМ!).

Этот пример нужен для осознания того, что могут проиграть и выиграть ОБА, а не только кто-то один.

В жизни лучше вообще конфликтов избегать . :)

В теории игр выделяются два поведения:

• Личные

• Вероятностные

При личных ходах выбор действия полностью зависит от игрока (шахматы).

При вероятностных – случайно (карты и другие азартные игры).

Существует понятие: оптимальная стратегия.

Это такая стратегия, при многократном повторении которой (при многократном повторении игры) игроку обеспечивается максимальный средний выигрыш.

Основной принцип, заложенный при построении теории игр: мы не рассчитываем на ошибку противника (не рассчитываем, что он глупее нас).

Если игра состоит из нескольких ходов, то для нее всегда известна стратегия, ведущая к выигрышу. (крестики-нолики)

Стратегия игрока А – А

Стратегия игрока В – В

В₁ В₂ * * * * В_n

A₁ a₁₁ a₁₂ a_1n

A₂ a_{21 *} a_2n

* * * *

* * * *

A_n a_m1 a_m2 a_mn

Каждой стратегии А можно сопоставить выигрыш игрока В. Для игр с нулевой суммой числа зеркальные.

Матрица при игре с «выкидыванием пальцев».

Если сумма выкинутых пальцев четная, то мы выиграли, а если нечетная – противник.

наилучший выигрыш для противника

- наилучший выигрыш для нас

Противник выберет стратегию 4 или 4, а мы выберем -3.

Противник будет пытаться максимизировать свой выигрыш и минимизировать наш.

Еще один пример: Рассмотрим следующую игру:

У противника есть 3 типа самолетов. У нас есть 3 типа вооружения.

Мы не знаем, какой тип самолетов применит противник, а он не знает, какое вооружение применим мы. (присутствует разная степень защиты самолетов от нашего вооружения).

Матрица сопоставления: соответствие выбранного самолета выбранному вооружению.

Вооружение – А_1, А₂, А₃

Самолеты - В_1, В₂, В₃

наилучший выигрыш для противника

- наилучший выигрыш для нас

Попробуем рассуждать:

Противник не глупее нас, и мы с ним оба не знаем, что предпримет и предпочтет другой.

Мы определяем некоторые а_ij, которые являются минимальным значением для каждой строки. a_i=mina_ij

Затем из этих решений мы выбираем те, что принесут нам максимальный результат вне зависимости от «вредности» противника.

ά=max(i)min(j)a_ij - это минимальный выигрыш, «нижняя цена игры», хотя можем получить и больше.

Аналогично и противник: в_i=max(j) a_ij

Минимаксный принцип: игра, для которой мы придерживаемся максиминной стратегии, а противник – минимаксной.

Для нас оптимальной является первая стратегия (в примере с «выкидыванием пальцев» ). Если мы все время будем ее применять, то противник это поймет и накажет нас, выбрав стратегию 2 (-3).

Наши шаги при выборе стратегии:

1. наш выбор стратегии: а₁₁

2. его выбор стратегии: а₁₂

3. наш выбор стратегии: а₂₂

4. его выбор стратегии: а₃₂

и непонятно, к чему придем.

Вернемся ко второму примеру: и для нас, и для противника оптимальная стратегия: а₂₂(0,7). ά=β=γ. Игры, где верхняя и нижняя цена игры равны, называются играми с седловой точкой. Для них характерно:

• Если любой из противников меняет стратегии, то неизбежно проигрывает.

• γ - чистая цена игры.

• Стратегия, соответствующая седловой точке, - ОПТИМАЛЬНА.

• Если один из игроков придерживается этого принципа, то другому игроку не может быть выгодно менять стратегию.

• Игры с Седловой точкой обладают устойчивостью.

• Решение надо искать в смешанных стратегиях.

Мы имеем стратегии: А_1, А₂,… А₃

Противник имеет стратегии: В_1, В₂,…В_n

Сопоставим вероятности выбора оптимальной стратегии:

S_A^*=(p_1;p_2; p_3;…p_n)

S_B^*=(q_1;q_2; q_3;…q_n)

Решением игры называется пара оптимальных стратегий S_A^* и S_B^*, таких что если один придерживается оптимальной смешанной стратегии, то другому не может быть выгодно отступать от этой стратегии.

Выигрыш соответствующего решения называется ЦЕНОЙ ИГРЫ.

Если один из игроков придерживается оптимальной смешанной стратегии, то выигрыш остается неизменным и равным γ (цене игры) вне зависимости от того, что делает другой игрок, если только тот не выходит за пределы своих активных стратегий.

Рассмотрим простейший случай:

Имеется игра 2х2

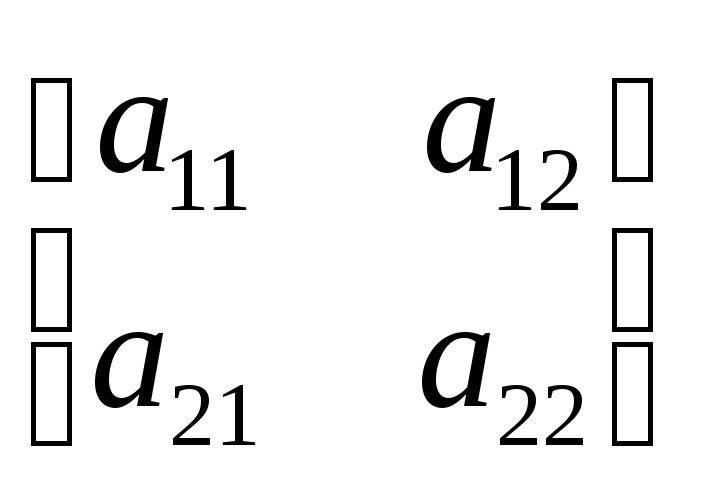Если есть седловая точка, то всё хорошо и дальше ничего делать не надо. Если нет, то ищем S_A^*=(p_1;p_2;) и S_B^*=(q_1;q_2;)

Мы применяем нашу оптимальную стратегию с вероятностью р₁а₁₁ и р₂а₁₂, а противник только с вероятностью р₁.

Чему равен средний выигрыш? γ= р₁а₁₁ + р₂а₂₁,

Если мы применим смешанную стратегию, а противник - стратегию В, то выигрыш будет: γ= р₁а₂₁ + р₂а₂₂

р₁ + р₂=1

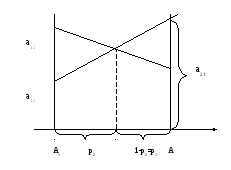
Если мы выбираем А₂, а противник – В₂,то схема будет такой.

Любой смешанной стратегией будет соответствовать точка А₁ и А_2.

N- максимально получаемый выигрыш вне зависимости от стратегии противника. .

Каждой стратегии В соответствует некоторая прямая.

S_A^*=p_1;p_2; p_3;…p_n

S_B^*=q_1;q_2; q_3;…q_n

S_A- обладает таким свойством, что если мы будем ее применять, то любое поведение противника обеспечит наш выигрыш, не меньший, чем цена игры.

Наш выигрыш при применении оптимальной смешанной стратегии:

p₁а₁₁+ p₂а₂₁+_…p_ma_m1γ (1 – противник использует В₁. Если противник будет применять В₂, то на месте этой единицы будет 2)

Это мат. ожидание выигрыша.

p₁а_1n+ p₂а_2n+_…p_ma_mnγ разделим все на γ

p₁+p₂+p_{3 …}+p_n=1

Обозначим х₁=р₁/γ х₂=р₂/γ х₃=р₃/γ

Получим

х₁а₁₁+ х₂а₂₁+_…х_ma_m11

….

….

х₁а_1n+ х₂а_2n+_…х_ma_mn1

L=x₁+x₂+…+x_m=1/γ

L→min; γ→max; значит наш выигрыш будет максимальным.

Пример (вспомним пример с пальцами )

Прибавим везде 5

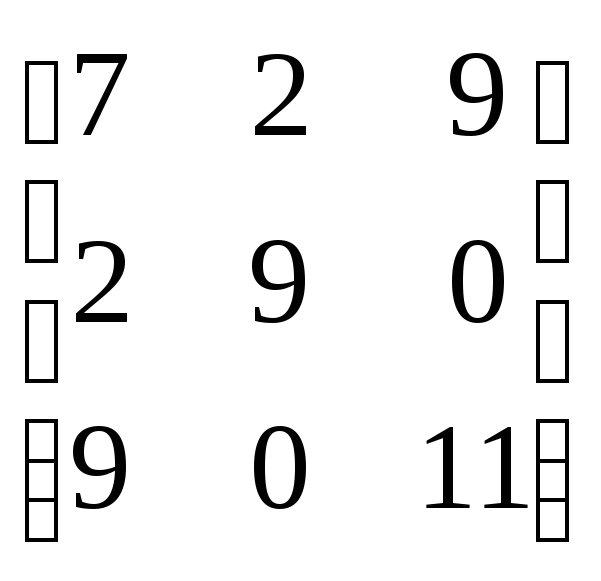
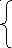
7х₁+ 2х₂+9х₃ 1

2х₁+ 9х₂ 1

9х₁+ +11х₃ 1

х₁ + х₂ +х_m 1→min

Решаем, находим х, интересующий нас: γ^'= γ+5

5