лекции, учебные пособия / конспект лекций / Lekcii / Лекция 8 (Соснин В

Критерий оптимальности – надежность (продолжение лекции 7)

Загрузка каждого узла должна быть меньше 1, поэтому имеем следующую систему ограничений в совокупности с критерием оптимальности:

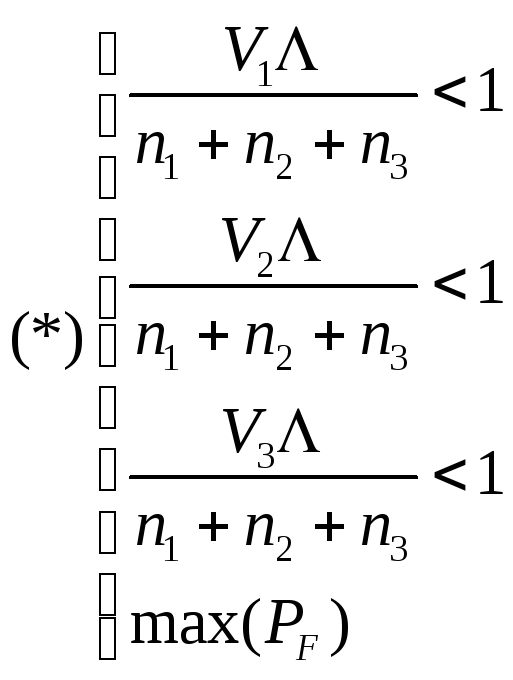
В результате решения системы (*) получаем вектор-решение (n₁ n₂ n₃)^-1

Где вероятность работоспособности системы:

n_min – минимальное количество исправных машин в каскаде (кластере).

Это показатель надежности для одного каскада.

Для системы из трех каскадов имеем:

Теперь учтем тот факт, что количество машин в кластере может быть равным нулю, тогда вероятность работоспособности системы имеет вид:

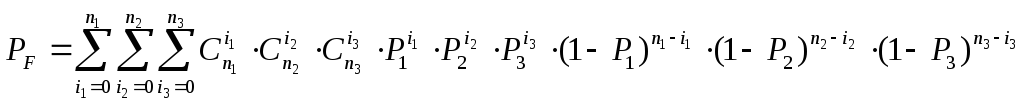
Эта формула решает проблему «чем больше машин, тем хуже надежность», появившуюся в первой формуле.

Теперь учтем, что количество ремонтеров в бригаде, обслуживающей систему, может быть меньше количества сломанных компонентов. Для этого рассмотрим систему из трех компьютеров. Пусть система работоспособна, если исправна хотя бы одна машина. Пусть система восстанавливаема. Тогда имеем 4 возможных состояния этой системы:

1. три компьютера исправны

2. два компьютера исправны

3. один компьютер исправен

4. все компьютеры исправны

Пусть λ – интенсивность отказа 1-й машины, μ – интенсивность восстановления 1-й машины одним ремонтером. Построим граф состояний и переходов:

Для каждого случая решается задача нахождения вероятностей каждого из состояний с использованием методов теории массового обслуживания.

Критерий оптимальности – производительность

Равновероятное распределение интенсивности запросов по кластерам

Интенсивность запросов в каждую машину системы равна:

Загрузка системы по узлам равна:

Время пребывания по узлам:

Среднее время пребывания запроса в системе

Нормализуем по худшему случаю. Пусть в машинах 1-го типа время пребывания самое большое, тогда:

T^α – нормализованное значение

Вероятностное распределение потока запросов по кластерам

β₁ – вероятность, что запрос направится после распределителя в кластер типа 1

β₂ – вероятность, что запрос направится после распределителя в кластер типа 2

β₃ – вероятность, что запрос направится после распределителя в кластер типа 3

β₁ + β₂ + β₃ = 1

Тогда вектор-решение системы (*) имеет вид: (n₁ n₂ n₃ β₁ β₂ β₃)^-1

Загрузка системы по узлам равна:

Время пребывания по узлам:

Среднее время пребывания в системе:

Нормализуем по худшему случаю. Пусть в машинах 1-го типа время пребывания самое большое, тогда:

T^α – нормализованное значение

Критерий оптимальности – стоимость

C^α = (n₁s₁ + n₂s₂ + n₃s₃)/C

Сразу получаем нормализованное значение

Многокритериальная задача