
Варианты к-р с решениями / 1 контра Сумина / Решения
.docВариант 1
№1
В урне 5 белых и 3 чёрных шара. Из урны вынимают сразу 2 шара. Найти вероятность того, что оба шара будут белыми.
Решение.
Общее число элементарных исходов
![]() ,
общее число благоприятных –
,
общее число благоприятных –
![]() .
Следовательно, искомая вероятность P=
m / n =
5 / 14.
.
Следовательно, искомая вероятность P=
m / n =
5 / 14.
№2
Вероятности попадания в цель при стрельбе из первого и второго орудий равны соответственно p1= 0,7, p2= 0,5. Найти вероятность попадания в цель при одновременном залпе обоих орудий хотя бы одним из них.
Решение.
Найдём вероятность события
![]() =
{ни одно орудие не попало}. Так как исход
выстрела для каждого орудия не зависит
от другого, то по теореме о произведении
вероятностей независимых событий,
=
{ни одно орудие не попало}. Так как исход
выстрела для каждого орудия не зависит
от другого, то по теореме о произведении
вероятностей независимых событий,
![]() 0,3
* 0,5 = 0,15. А тогда искомая вероятность
равна
0,3
* 0,5 = 0,15. А тогда искомая вероятность
равна
![]() .
.
№3
Имеется два одинаковых ящика с наборами деталей. Вероятность того, что деталь из первого ящика стандартная, равна 0,8, а из второго – 0,9. Найти вероятность того, что из наугад выбранного ящика будет извлечена стандартная деталь.
Решение. Пусть событие A = {из наугад выбранного ящика извлечена стандартная деталь}, гипотеза B1 = {деталь взята из первого ящика} и гипотеза B2 = {деталь взята из второго ящика}. Заметим, что P(B1) = P(B2) = 1 / 2. Кроме того, они образуют полную группу попарно несовместных событий, а событие A наступает только после появления одного из них. Значит, справедлива формула полной вероятности:
![]()
Найдём условную вероятность P(A|B1). Для начала запишем, что событие A|B1 = {деталь из первого ящика стандартная}. Следовательно, P (A|B1)= 8 / 10. Аналогично найдём, что P (A|B2)= 9 / 10. Таким образом,
![]()
№4
Игральная кость брошена 8 раз. Найти вероятность того, что шестёрка появится не менее 4-х, но не более 6-ти раз.
Решение. Задача удовлетворяет схеме Бернулли, где n= 8, событие A= {появление шестерки в любом броске} может наступить с постоянной вероятностью p= 1 / 6. Найдём:
![]()
![]()
![]()
Т.к. найденные вероятности принадлежат несовместным событиям, то искомая вероятность равна
![]()
№5
У клевера красного бывает в среднем 84% позднеспелых растений. Какова вероятность того, что 152 растения из 180 растений клевера, отобранных случайным образом, являются позднеспелыми?
Решение. Вероятность того, что случайно выбранное растение позднеспелое, равна 0,84 и не меняется при любом количестве отобранных растений. Следовательно, условие задачи удовлетворяет схеме Бернулли, где n= 180, p= 0,84, q= 0,16, m= 152. Требуется подсчитать вероятность P180(152).
Проверим применимость приближённой формулы Пуассона. Имеем: λ= np= 151,2 > 10. Значит, формулу Пуассона использовать нельзя!
Проверим применимость приближённой формулы Муавра–Лапласа (локальной формы, т.к. интересуемся конкретным значением случайной величины): npq= 24,2 > 20. Следовательно, формулу можно использовать. Находим аргумент
![]()
По таблице находим соответствующее значение функции Лапласа: φ(0,163) ≈ 0,3937 и искомую вероятность:
![]()
№6
Какое минимальное количество раз нужно подбросить монету, чтобы с вероятностью не меньшей 0,95 отклонение относительной частоты выпадения орла от вероятности его выпадения не превосходило 0,01?
Решение. При каждом броске вероятность выпадения орла постоянна и равна p= 1 / 6. Условие удовлетворяет схеме Бернулли. Применим интегральную формулу Муавра–Лапласа для вычисления вероятности отклонения величины m / n от постоянной вероятности p:
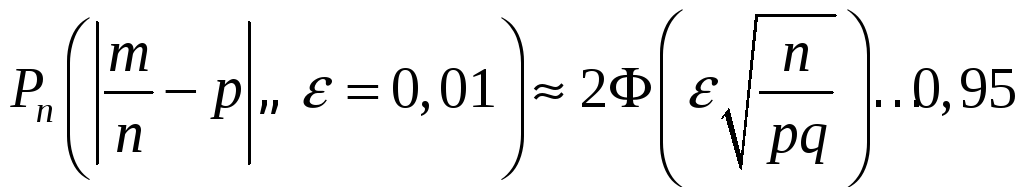
Нам известно значение функции Ф(x)=0,95/2=0,475. По таблице находим, что x при этом примерно равен 1,960. Из формулы выражаем и находим n:
![]()
Убедимся в применимости вышеуказанной формулы: npq= 560*5/36 ≈ 77 > 20. Следовательно, наименьшее количество подбрасываний равно 560.
Вариант 2
№4
В институте на факультете насчитывается 1825 студентов. Какого вероятность того, что 1 сентября является днём рождения одновременно 4-х студентов факультета?
Решение. Будем считать, что в году 365 дней и каждый человек с равной вероятностью мог родиться в любой из них. Следовательно, вероятность родиться 1 сентября для всех одинакова и равна p= 1 / 365. Заметим, что задача удовлетворяет схеме Бернулли, где в качестве независимого испытания рассматривается определение дня рождения следующего студента, т.е. n= 1825 и m= 4. Для нахождения искомой вероятности воспользуемся приближённой формулой.
Проверим применимость формулы Пуассона: λ= np= 5 < 10. Следовательно, формула применима. Из таблицы находим p4(5)= 0,175. Это окончательный ответ.
Вариант 3
№6
Всхожесть некоторого сорта семян на данном участке составляет в среднем 80%. Какова вероятность того, что прорастёт не менее 76% из 150 посеянных семян?
Решение. Условие задачи удовлетворяет схеме Бернулли, причём n= 150, p= 0,8, q= 0,2. Воспользуемся приближённой интегральной формулой Муавра–Лапласа (npq= 24 > 20, np= 120, m1= 150*0,76= 114):
![]()
По таблице находим: Φ(–1,225) ≈ –0,3895. Окончательный ответ:
![]()
Вариант 5
№1
Д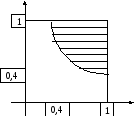 ве
точки независимо друг от друга наудачу
выбираются на отрезке [0; 1]. Найти
вероятность того, что произведение
координат точек будет больше 0,4.
ве
точки независимо друг от друга наудачу
выбираются на отрезке [0; 1]. Найти
вероятность того, что произведение
координат точек будет больше 0,4.
Решение.
Пусть одна точка имеет координату x,
а другая – координату y.
Они независимы друг от друга. Всевозможные
комбинации пар (x;
y) на указанном
отрезке можно проиллюстрировать
геометрической областью, заключённой
внутри квадрата с длиной стороны 1. Из
условия имеем:
![]() ,
или
,
или
![]() .
Этому неравенству соответствует
заштрихованная часть квадрата. Искомая
вероятность равна отношению площадей,
или площади заштрихованной части:
.
Этому неравенству соответствует
заштрихованная часть квадрата. Искомая
вероятность равна отношению площадей,
или площади заштрихованной части:
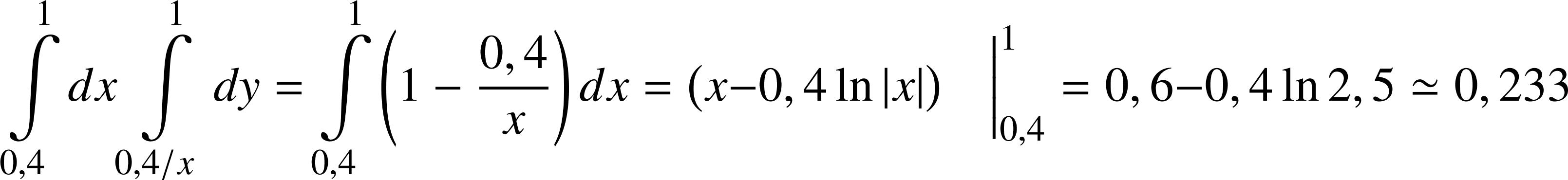
№2
В коробке находятся 4 белых, 3 синих и 2 чёрных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что 1-й шар будет белым, 2-й – синим, а 3-й – чёрным?
Решение. {Задача на условные вероятности.} Пусть события A1 = {первый извлечённый шар белый}, A2 = {второй извлечённый шар синий} и A3 = {третий извлечённый шар чёрный}. Интересующее нас событие B= A1A2A3. По теореме о произведении вероятностей,
![]()
Находим P(A1)= 4 / 9, P(A2|A1)= 3 / 8 и P(A3|A1A2)= 2 / 7. Тогда P(B)= 1 / 21.
№3
В сборочный цех завода поступает 40% деталей из 1-го цеха и 60% – из 2-го цеха. В 1-м цехе 90% производимых деталей стандартные, а во 2-ом – 95%. Найти вероятность того, что наудачу взятая сборщиком деталь окажется стандартной.
Решение. Пусть событие A = {наудачу взятая деталь стандартная}, гипотеза B1 = {деталь произведена в первом цеху} и гипотеза B2 = {деталь произведена во втором цеху}. Заметим, что P(B1) = 2 / 5 и P(B2) = 3 / 5. Кроме того, они образуют полную группу попарно несовместных событий, а событие A наступает только после появления одного из них. Значит, справедлива формула полной вероятности:
![]()
Найдём условную вероятность P(A|B1). Для начала запишем, что событие A|B1 = {наудачу взятая из первого цеха деталь стандартная}. Следовательно, P (A|B1)= 9 / 10. Аналогично найдём, что P (A|B2)= 19 / 20. Таким образом,
![]()
№4
Начинающий шахматист играет 8 шахматных партий против членов шахматного клуба. Играет он плохо, поэтому вероятность выигрыша им каждой партии равна 0,01. Найти вероятность того, что этот шахматист выиграет хотя бы одну партию.
Решение. Исход каждой сыгранной партии не зависит ни от какого другого исхода. Следовательно, имеем 8 независимых испытаний, в каждом из которых событие A= {шахматист выигрывает} может наступить с постоянной вероятностью 0,01. Воспользуемся формулой Бернулли. Найдём сначала вероятность того, что шахматист проиграет все партии:
![]()
А тогда вероятность выиграть ему хотя бы одну партию равна
![]()
№5
Передаваемые знаки на линии связи искажаются независимо друг от друга. Вероятность искажения знака равна 0,03. Найти вероятность того, что в сообщении из 800 знаков будет искажено ровно 25 знаков.
Решение. Условие задачи удовлетворяет схеме Бернулли. Требуется найти P800(25), причём n= 800, p= 0,03, q= 0,97. Проверим применимость приближённой формулы Пуассона: λ= np = 800*0,03 = 24 > 10. Следовательно, применять формулу Пуассона нельзя!
Проверим применимость локальной формулы Муавра–Лапласа: npq= 800*0,03*0,97 = 23,28 > 20. Следовательно, да. Находим x (m=25)
![]()
По таблице ищем: φ(0,207) ≈ 0,39047 и считаем искомую вероятность:
![]()
№6
При установившемся технологическом режиме завод выпускает в среднем 70% продукции 1-го сорта. Определить вероятность того, что из 1000 изделий число первосортных заключено между 680 и 730.
Решение. Условие задачи удовлетворяет схеме Бернулли, причём n= 1000, p= 0,7, q= 0,3. Воспользуемся приближённой интегральной формулой Муавра–Лапласа (npq= 210 > 20, np= 700, m1= 680, m2= 730):
![]()
По таблице находим: Φ(–1,380) ≈ –0,41621, Φ(2,070) ≈ 0,48077. Окончательный ответ:
![]()
