Справочный материал / Предел / Предел функции.Определения. Свойства предела

Предел функции

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Преде́л фу́нкции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке x₀ если для всех значений x, достаточно близких к x₀, значение f(x) близко к A.

Определения

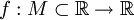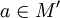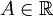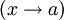• (определение по Коши, ε−δ—определение) Пусть дана функция и — предельная точка множества M. Число называется пределом функции f при x, стремящемся к a , если

• (окрестностное определение) Пусть дана функция 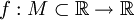и — предельная точка множества M. Число называется пределом функции f при x, стремящемся к a 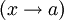, если для любой окрестности V(A) точки A существует проколотая окрестность 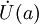точки a такая, что

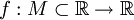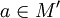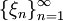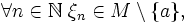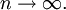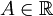• (определение по Гейне) Пусть дана функция и — предельная точка множества M. Будем называть последовательностью Гейне, если и при Число называется пределом функции f при x, стремящемся к a 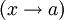тогда и только тогда, когда для любой последовательности Гейне имеем

при

Замечания

• Все данные выше определения предела функции в точке эквивалентны.

• Если предел функции f при 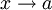существует и равен A, пишут

• Предел может быть односторонним или двусторонним.

Предел вдоль фильтра

Определение фильтра

Основная статья: Фильтр (математика)

Пусть дано множество A. Система множеств называется фильтром на A, если

• 

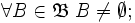
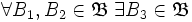• такой, что

Определение предела

Пусть и — фильтр на M. Число является пределом функции f по фильтру если

Пишут:

Примеры

Обычный предел

Пусть дано топологическое пространство , и Пусть Тогда система множеств

является фильтром и обозначается Данное выше определение предела совпадает с пределом по фильтру

Односторонние пределы

Основная статья: Односторонние пределы

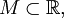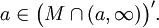• Пусть и Тогда система множеств

является фильтром и обозначается или Предел называется правосторонним пределом функции f при x стремящемся к a.

• Пусть и Тогда система множеств

является фильтром и обозначается или Предел называется левосторонним пределом функции f при x стремящемся к a.

Пределы на бесконечности

Основная статья: Пределы функции на бесконечности

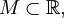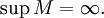• Пусть и Тогда система множеств

является фильтром и обозначается или Предел называется пределом функции f при x стремящемся к бесконечности.

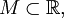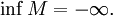• Пусть и Тогда система множеств

является фильтром и обозначается Предел называется пределом функции f при x стремящемся к минус-бесконечности.

Предел последовательности

Основная статья: Предел последовательности

Система множеств где

является фильтром и обозначается Функция называется числовой последовательностью, а предел пределом этой последовательности.

Интеграл Римана

Основная статья: Интеграл Римана

Пусть Назовём размеченным разбиением отрезка [a,b] коллекцию точек Назовём диаметром разбиения T число Тогда система множеств

является фильтром в пространстве всех размеченных разбиений [a,b]. Определим функцию равенством

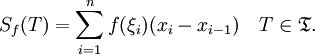
Тогда предел называется интегралом Римана функции f на отрезке [a,b].

Свойства пределов числовых функций

Пусть даны функции и Тогда

• Предел единственнен, то есть

• Сходящаяся функция локально сохраняет знак. Более обще,

где - проколотая окрестность точки a.

• В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:

• Сходящаяся функция локально ограничена в окрестности предельной точки:

• Операция взятия предела сохраняет нестрогие неравенства.

• Предел суммы равен сумме пределов:

• Предел разности равен разности пределов:

• Предел произведения равен произведению пределов:

• Предел частного равен частному пределов.