Лекции МГУ / EM07

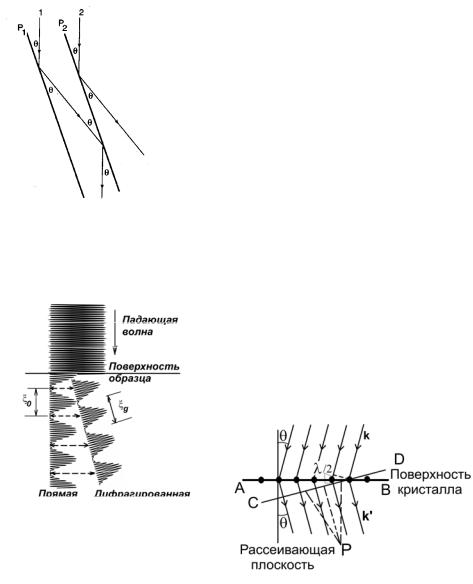
Лекция 7.

ЭЛЕМЕНТЫ ДИНАМИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ.

Экстинкция. Колонковое приближение. Уравнения Хови-Уэлана. Решение уравнений Хови-Уэлана. Интенсивность прямого и дифрагированного пучков. Эффективный вектор отклонения. Лауэ зоны. Двойная дифракция. Дифракция в многофазных системах

Экстинкция

При рассмотрении амплитуды рассеяния в Л6 образец считался тонким, так, что потерями интенсивности в прямом и дифрагированном пучке пренебрегалось. Вместе с тем, при увеличении толщины образца четкость ДК уменьшается, а интенсивность

			падает. Наиболее простое представление о динамических
			эффектах можно получить, посмотрев на рис. 7.1.
			Рассеяние на атомных плоскостях приводит к дифракции
			и	выбыванию		дифрагированного		пучка	из
			первоначального направления. Как будет показано ниже,
			достаточно		небольшого количества			рассеивающих
			плоскостей, чтобы прямая волна полностью перешла в
			дифрагированную. Однако, дифрагированный пучок
			имеет возможность вновь рассеяться и вернуться, таким
			образом, в прямой пучок. Т.о., динамический эффект
			состоит в непрерывном динамическом изменении
			интенсивности, как прямого, так и обратного пучка, по
	Рис. 7.1. Иллюстрация	к	мере прохождения образца. При отсутствии неупругих
динамическим			потерь этот		процесс,		называемый экстинкцией		и
эффектам.			иллюстрируемый на рис. 7.2, может продолжаться
			многократно.		Возникает		подобие стоячих продольных

				волн (биений) интенсивности с периодом равным
				длине экстинкции, ξ0 для прямого пучка и		ξg для
				дифрагированного с вектором g.
				Динамическими эффектами можем пренебречь, если
				толщина образца меньше длины экстинкции. Оценим
					эту	длину
					экстинкции.
					Представим
					себе	случай
					брэгговского
					рассеяния
					плоскостями,
					перпендикуля
	Рис. 7.2.
						рными
Перераспределение
					поверхности,
интенсивности между
					рис.7.3	[16].
прямой и				Рис.7.3. Френелевское построение
					Возмущение в
дифрагированной волнами
				брэгговской отраженной волны.	некоторой
					точке	Р

впереди волнового фронта CD будет определяться суммой парциальных амплитуд с

3

Рис. 7.6. Амплитудно-фазовая диаграмма вкладов плоскостей.

Рис. 7.5. Вклады в дифрагированную волну от плоскостей, параллельных поверхности АВ.

учетом разности фаз. Мысленно разделим плоский фронт CD на зоны Френеля, края

			которых отличаются сдвигом фаз в 1800 (см.
			рис.7.4а. [16] и, более подробно, -					Ландсберг,
			Оптика). Вклады парциальных волн можно
			просуммировать с помощью амплитудно-фазовой
			диаграммы,	где	каждая		составляющая
			представлена	вектором,		длина		которого
			пропорциональна		амплитуде,		а	угол		с
			направлением падающей волны равен разности
			фаз. Амплитудно-фазовая диаграмма для такого
			случая имеет форму спирали и показана на рис.
			7.4б. Результирующая амплитуда рассеяния
			сдвинута по фазе на 900 относительно
			направления падающей волны и равна по
			величине половине		составляющей			от	первой
			полупериодной зоны. Представляя фронт в виде
Рис.7.4. Зоны Френеля - а) и б) -			пластины CD толщиной dx, амплитуда рассеяния
			для единичной	амплитуды		падающего			пучка
амплитудно-фазовая диаграмма			будет равна
			dψg = iλ(fpdx)exp (2πikr),				(7.1)

где fpdx – амплитуда рассеяния на единицу площади плоскости CD, а r – расстояние от точки Р до этой плоскости. В действительности, рассеивают элементарные ячейки на плоскости АВ, и если n – число элементарных ячеек на единицу площади на АВ, то

fpdx = (Fgn)/cosθ,

(7.2)

где Fg – структурный фактор (6.24) для рефлекса g. Таким образом,

dψg = iqexp (2πikr),	(7.3)
где q = nλ Fg/cosθ.	(7.4)

Физический смысл безразмерного параметра q – доля амплитуды первичного пучка, которая выбывает при дифракции на атомах плоскости АВ.

Радиус 1-й полупериодной зоны Френеля R = (λr)1/2, рис.7.4а, и для r = 1см величина R

2·10-5 см, что весьма велико по сравнению с раз мер ом ато ма, т.е. дис крет ным хара ктер

ом плоскости рассеяния, состоящей из атомов, можно пренебречь.

Для типичных рефлексов низкого порядка в металлах Fg 10-7 см, n 1015 см –2, λ 0.0037 нм для Е0=100 кэВ, и cosθ 1. Тогда q 4·10-2. Поэтому пучок должен пройти примерно только 25 плоскостей, чтобы все электроны претерпели дифракцию. Для сравнения – в случае рентгеновской дифракции число плоскостей должно быть ~104. Т.о. потерями интенсивности в электронной дифракции можно пренебречь только в случае очень тонких кристаллов.

4

Поскольку имеются отклонения от точных условий Брэгга, то необходимо учитывать разность фаз между составляющими от разных плоскостей. Разность фаз между составляющими от 1-й и m-й плоскостей равна -2πK’·rm, где rm взято вдоль k’, т.е. вдоль направления дифрагированного пучка, рис. 7.5 [16]. Т.к. каждая составляющая равна iq, амплитудно-фазовая диаграмма будет правильным многоугольником или (поскольку q мало) окружностью с максимальной амплитудой 2mq/π, рис.7.6 [16]. Число плоскостей, дающих вклад в формирование дифрагированного пучка единичной амплитуды, равно m = π/2q. Длина экстинкции ξg определяется как удвоенное соответствующее расстояние в кристалле, т.е.

ξg = πa/q,

(7.5)

где а – расстояние между плоскостями АВ. Подставляя выражение для q и положив n/a = 1/Vc, где Vc - объем элементарной ячейки, получаем

ξg = πVccosθ/(λFg)

(7.6)

Длина экстинкции служит мерой уменьшения интенсивности пучка с числом пройденных дифрагированным пучком слоев или с толщиной образца. Прямой пучок является частным случаем, соответствующим g = 0. Для отражений низкого порядка длина экстинкции составляет несколько десятков нм.

Колонковое приближение (column approximation)

В колонковом приближении выполняются большинство расчетов интенсивности

								дифрагир
								ованного
								пучка.
									Оно
								основыва
								ется	на
								том,	что
								амплитуд
									а
								выходяще
								й	из
		Рис.7.7. Конус зон Френеля						образца
					Рис. 7.8. Схема колонкового
								волны,
					приближения
									см.

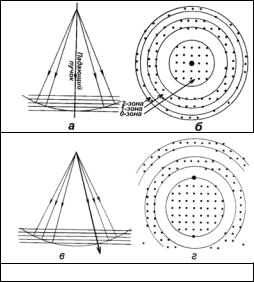
рис.7.7, определяется вкладом всех ячеек образца, лежащих в конусе с угловым раствором, определяемым несколькими зонами Френеля, диаметр которых, в свою очередь, главным образом определяется длиной волны λ. Для первой зоны R = (λt)1/2, λ = 3.7 пм (Е0=100 кэВ), t = 100 нм, R 0.6 нм., а радиус области из нескольких зон ~ 2 нм. Т.о. раствор конуса мал, что дает основание для колонкового приближения, рис. 7.8.

Уравнения Хови-Уэлана

Разделив кристалл, имеющий n элементарных ячеек на единицу площади поверхности, на слои толщиной а, параллельные поверхности, и с учетом (7.4-7.6) для амплитуды дифрагированного пучка, обозначаемой здесь как φg, в приближении

плоских волн получаем
φg = (πai/ξg) exp(2πikDr)exp(-2πiKrn),	(7.7)

где rn- означает позицию элементарной кристаллографической ячейки. Полная волновая функция есть суперпозиция прямого и дифрагированных пучков:

5

ψT = φ0exp(2πiχ0r) + φg1exp(2πiχg1r) + φg2exp(2πiχg2r) + …

(7.8)

с векторами χg1, χg2 и т.д. Вектор χ0 соответствует g = 0, т.е. началу координат обратной решетки. Ограничимся в последующем рассмотрении только одним дифрагирующим пучком помимо прямого, т.е. т.н. двухпучковым приближением, которое легко и часто реализуется в эксперименте: наклоняем кристалл так, что в ДК присутствует только один сильный рефлекс с вектором отклонения s =0. Все другие пучки слабы, т.е. s >> 0 либо <<0. Соответственно, в динамической картине перекачки интенсивности их вклад

тоже будет мал. Тогда, разделив образец на слои толщиной dz, изменения амплитуд φg и φ0

d φg = {(πi/ξ0)φg + (πi/ξg)φ0exp[2πi(χ0-χD) r] }dz	(7.9)
и
d φ0 = {(πi/ξ0)φ0 + (πi/ξg)φg exp[2πi(χD-χ0) r]}dz.	(7.10)

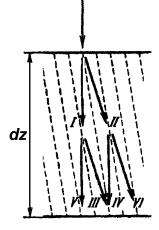
Первый член описывает вклад рассеяния в прямом направлении, а второй – вклад

брэгговского рассеяния, а					χ0-χD и χD-χ0 – соответствующее изменение волнового
					вектора. Длина экстинкции ξ0 соответствует рассеянию
					вдоль движения пучка, в том числе и дифрагированного
					(IÆV, IIÆVI, рис.7.9), а ξg – рассеянию с изменением
					волнового вектора на g, (IÆIII, IIÆIV, рис.7.9). Уравнения
					(7.9-10) могут быть преобразованы в систему динамически
					связанных уравнений для φ0 и φg. Вспоминая, что K = kD-k0
					= (g + s) для идеального кристалла, а также в силу малости
					углов Брэгга, получаем:
					d φg/dz = (πi/ξ0)φg + (πi/ξg)φ0exp(-2πisz)	(7.11а)
					d φ0/dz = (πi/ξ0)φ0 + (πi/ξg)φg exp(2πisz).	(7.11б)
					Уравнения (7.10) называют уравнениями Хови – Уэлана
					[22], а иногда Дарвина-Хови-Уэлана, поскольку Дарвин
					[23] развил динамическую теорию для рентгеновских
					лучей еще в 1914.
	Рис. 7.9. Динамическое				Делая подстановку,
					φ0s = φ0exp(-πiz/ξ0)	(7.12а)
	перерассеяние в 2-х				φgs = φgexp(2πisz -πiz/ξ0),	(7.12б)
	пучковом
	приближении.				уравнения (7.11) преобразуются к виду
					dφgs/dz = (2πis)φgs + (πi/ξg)φ0s	(7.13а)
		dφ0s/dz = (πi/ξg)φgs.
						(7.13б)

Поскольку φ0 и φ0s, а также φg и φgs отличаются только фазовым фактором, который исчезает при вычислении интенсивностей, мы будем игнорировать различие. Тогда уравнения (7.13) могут быть скомбинированы и получено уравнение 2-го порядка для

φ0.
d2φ0/dz2 - 2πis dφ0/dz + (π2/ξg2)φ0 = 0.	(7.14)
Решение уравнений Хови-Уэлана
Решение уравнения (7.14) имеет вид
φ0 = С0exp(2πiγz).	(7.15)
Подставляя в (7.14), получаем алгебраическое уравнение
γ2 - sγ - 1/(4ξg2) = 0.	(7.16)

Поскольку φ0s и φgs, а следовательно и φ0 и φg, связаны уравнением (7.13), то,

подставляя (7.15) в (7.13), имеем
φg = 2ξgγС0exp(2πiγz).	(7.17а)
Мы можем также как и в (7.15) ввести

6

	φg = Сgexp(2πiγz),	(7.17б)
Тогда	Сg/С0 = 2ξgγ	(7.18)
	Корнями алгебраического уравнения (7.16) являются
	γ1,2 = [s ± (s2 + 1/ξg 2)1/2]/2.	(7.19)

Т.о. имеются две амплитуды для φ0 и для φg в соответствии с (7.15) и (7.17,18).

	Каков физический смысл γ1 и γ1? Отметим прежде, что
	γ1 + γ2 = s,	(7.20)
т.е. чисто геометрическая величина, а
	γ1 · γ2 = - 1/(4ξg2),	(7.21)
свойство материала.
Удобно ввести безразмерный параметр
	w=sξ.	(7.22)
Тогда	Сg,1 /С0,1 = 2ξgγ1 = w – (w2+1)1/2	(7.23а)
и	Сg,2 /С0,2 = 2ξgγ2 = w + (w2+1)1/2.	(7.23б)
Другой удобной подстановкой
	w = cot β,	(7.24)

мы определяем величину β. Далее мы накладываем ограничения на абсолютное значение амплитуд, так чтобы выполнялось соотношение

С0,12 + Сg,12 = 1 = С0,22 + Сg,22 .		(7.25)
И тогда, подставляя (7.24) в (7.23), получаем,
С0,1	= сos (β/2), Сg,1 = - sin (β/2),	(7.26а)
С0,2	= sin (β/2), Сg,2 = cos (β/2).	(7.26б)

При этих ограничениях выполняется условие того, что в 2-х пучковом приближении вероятность найти электрон либо в прямом, либо в дифрагированном пучке, остается постоянной и равной единице (|ψT|2 = 1).

Каждое значение γ дает различное значение k (k1 и k2).

Поскольку имеется две амплитуды для прямого и дифрагированного пучка, то имеется и две функции, отвечающие (7.8). Ограничиваясь двумя членами в (7.8),

получаем:
b1(k1,r) = C0,1exp(2πik1r) + Cg,1exp[2πi(k1	+ g)r]	(7.27а)
b2(k2,r) = C0,2exp(2πik2r) + Cg,2exp[2πi(k2	+ g)r].	(7.27б)

Это две функции блоховского типа. Полная функция может быть как одной из них, так и их комбинацией. Представим ψT как комбинацию

ψT = A1b1 + A2b2.	(7.28)
Подставляя значения для С (7.26), получаем
ψT = A1{сos (β/2)exp(2πik1r) - sin (β/2)exp[2πi(k1 + g)r]}
+ A2{sin (β/2)exp(2πik2r) + cos (β/2)exp[2πi(k2 + g)r]}	(7.29)
Преобразуем (7.29) к виду
ψT = {A2sin (β/2)exp(2πik2r) + A1сos (β/2)exp(2πik1r)}
+ {A2cos (β/2)exp(2πik2r)- A1sin (β/2)exp(2πik1r)} exp(2πigr).	(7.30)

Только второй член зависит от g, поэтому он должен быть амплитудой φg. Мы знаем,

что на поверхности образца (r =0) φ0 =1 и φg = 0. Откуда следует, что
A1 = сos (β/2) и A2 = sin (β/2)	(7.31)

Т.е. A1 и A2 зависят от s, согласно (7.24) и (7.22), и, таким образом, их можно изменять контролируемым образом, например, наклоном образца.

С учетом подстановки (7.12) полная волновая функция (7.9) приобретает вид

ψT = φ0exp(2πkr) + φgexp[2π(k+g)r],

(7.32)

7

где мы заменили χ0 =k, χg1=k+g+s и член содержащий s после замены (7.13) исчезает. Сопоставляя (7.32) с (7.30) и учитывая (7.31), получаем

φg = sin (β/2)сos (β/2){exp[2πi(k2-K)r] - exp[2πi(k1-K)r]}

(7.33)

Поскольку мы рассматриваем только z-компоненту, мы знаем из уравнений (7.15) и (7.17), что экспоненциальный член должен иметь фазу 2πiγz, т.е.

(k2-K)z = γ2, и (k1-K)z = γ1

(7.34)

Таким образом, k1,2 связаны с γ1,2 и амплитуда φg в (7.33) есть комбинация членов, содержащих k1 и k2. Ур-е (7.33) можно переписать как

	φg	= + i sin β sin(πz∆k) exp(πisz)	(7.35)
и	φ0	= {cos(πz∆k) – i cos β sin(πz∆k)} exp(πisz),	(7.36)
где ∆k = |k2 – k1|.
	Интенсивность прямого и дифрагированного пучков. Эффективный вектор
		отклонения
Заметим, что согласно (7.34)
	∆k = |k2 – k1| = ∆γ = γ2 - γ1.		(7.37)
Тогда, в соответствии с (7.19) и (7.22)
	∆k = (w2 + 1)1/2/ξg.		(7.38)

Интенсивность дифрагированного пучка на нижней стороне образца, т.е. при z = t, по

(7.35)

Ig = |φg |2	= sin2β sin2(πt∆k)	(7.40a)
Ig = |φg |2	= sin2[πt(w2 + 1)1/2/ξg] /(w2 + 1)	(7.40б)

Сопоставляя с (6.43), можем записать интенсивность, выразив аргумент через

эффективный вектор отклонения

seff = (w2	+ 1)1/2/ξg ,	(7.41)
и интенсивность
Ig = |φg |2	= (πt/ ξg)2 sin2[πt seff ] /( πt seff )2	(7.42а)
Соответственно,
I0 = 1 - Ig = 1 - (πt/ ξg)2 sin2[πt seff ] /( πt seff )2		(7.42б)

Из (7.41) следует, что эффективный вектор отклонения никогда не равен нулю. Даже в

том случае, когда s=0 и, по (7.22), w=0, seff = 1/ξg.

Выражения (7.42) особенно просты для случая s=0:

Ig	= sin2[πt/ξg]	(7.43а)
I0	= 1 - sin2[πt/ξg]	(7.43б)

Эти уравнения содержат только одну переменную

– t. Мы видим, что на поверхности Ig = 0, а также при t кратном ξ g. Напротив, I0 = 1 на этих глубинах, как это иллюстрируется рис. 7.2. Такое поведение аналогично эффекту связанных гармонических осцилляторов.

Лауэ зоны

В Л6 мы выяснили, что электронограмма – это

Рис.7.10. Лауэ-зоны. сечение обратной решетки сферой Эвальда, которая имеет радиус существенно больший, чем

период обратной решетки. Это сечение мы называли зоной. Однако, несмотря на большой радиус, на дифракционной картине проявляются рефлексы других плоскостей

8

или зон, параллельных основной, называемой нулевой зоной, как это иллюстрируется на рис. 7.10. Происходит это, конечно, вследствие конечной кривизны сферы Эвальда. Нулевая зона содержит узел 000. Последующие плоскости, пересекающие сферу Эвальда по окружности, называют, соответственно, первой, второй и т.д. зонами. Рефлексы ненулевых Лауэ-зон обычно появляются на ДК при «несимметричных» ориентировках кристалла, когда ось нулевой зоны несколько отклоняется от направления первичного пучка.

Двойная дифракция

Как было видно из рассмотрения динамических эффектов, взаимодействием прямого и дифрагированных пучков пренебрегать нельзя. Качественным следствием

этого

является

двойное

отражение,

которое

приводит

к

усреднению

интенсивностей

рефлексов,

усложняющему

определение

структурного фактора по интенсивностям

рефлексов

с

использованием формул

кинематической теории.

Помимо этого, на ДК возникают

дополнительные или экстра-рефлексы в

Рис. 7.11. Схема двойной дифракции.

том случае, когда имеется геометрическая

возможность лучу, дифрагировавшему на

семействе

плоскостей

(h1k1l1)

с

межплоскостным

расстоянием

d1,

вторично

дифрагировать

на

семействе

плоскостей

(h2k2l2) с

другим

межплоскостным

расстоянием d2, рис.7.11, или на

плоскостях того же семейства, но

несколько

иначе

ориентированных,

что реализуется, например, в

двойниках.

Такая

возможность

Рис.7.12. Двойное рассеяние с

связана, с одной стороны, с малыми

результирующим рефлексом в положении

значениями

брэгговских углов

для

запрещенного рефлекса (00.1) в гпу решетке.

электронов, а с другой – наличием

локальных

малоугловых

разориентировок

кристаллитов

и

изгибов пленки, увеличивающих вероятность одновременного удовлетворения условиям Брэгга для различных семейств плоскостей.

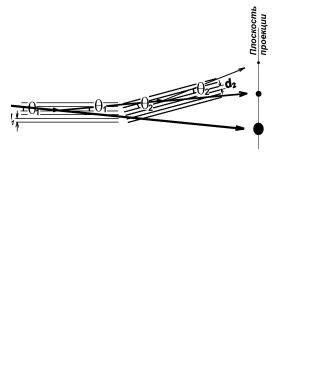
Экстра-рефлекс может при этом совпадать с запрещенным рефлексом для данной решетки из-за Fhkl =0. Однако, в любом случае радиус вектор должен быть равен сумме разрешенных векторов. В частности, на рис. 7.12а показаны стрелками пятна в положении запрещенных (00.1) рефлексов в ГПУ-структуре сплава на основе Со, а на рис.7.12б показано, что эти пятна являются рефлексами двойного отражения по схеме (00.1) = (10.2) + (-10.-1) [17].

Дифракция в многофазных системах

Дифракционная картина в образце, содержащем несколько различных ориентаций кристаллов или n фаз, является, по сути, суперпозицией n независимых

9

электронограмм. Пример ДК от преципитата Mg2Si в матрице Al с ориентацией (001) приведен на рис.7.13 [16].

Рис.7.13. ДК от Mg2Si в матрице Al с ориентацией (001). а) – картина первичной дифракции, б) – двойная дифракция, когда пятно Р является вторичным источником , в) суммарная ДК, 1-рефлексы Al, 2- рефлексы Mg2Si, 3- пятна двойной дифракции.

10