ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

= U A ,

Z a

= U B ,

Zb

= U C .

Z c

6.4. Расчет соединения звезда–звезда без нулевого провода

6.4.1.Симметричная нагрузка (цепь)

В случае симметричной цепи расчет токов в фазах нагрузки сводится к расчету соединения звезда-звезда с нулевым проводом, как это было показано в пункте 6.3:

I A = I a = U a Z a

I B = I b = U b Z b

I C = I c = U c Z c

6.4.2. Несимметричная нагрузка (цепь)

В случае несимметричной цепи напряжение на фазе нагрузки не равно соответствующему напряжению источника. Для определения

искомого тока I A = I a =	U	a ,	I B = I b =	U	b	и I C = I c = U c необходи-
	Z a			Z b		Z c

мо отыскать фазное напряжение на нагрузке.

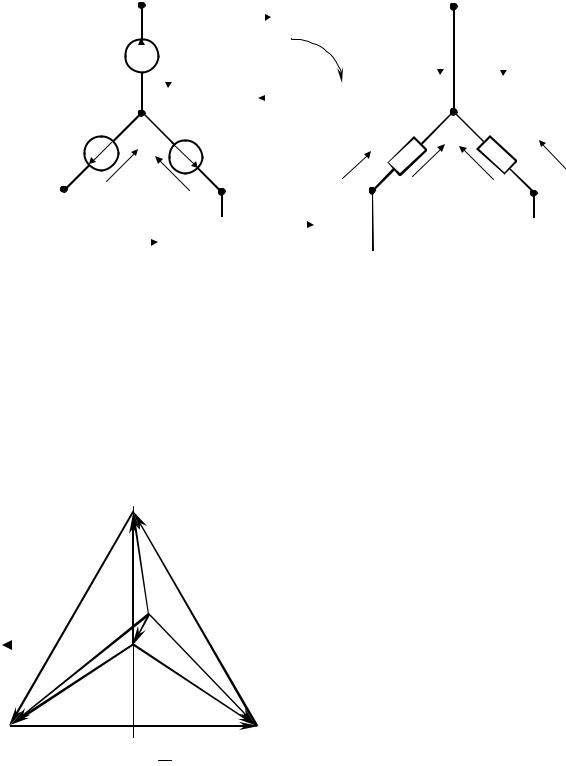
Для этого следует записать уравнение по второму закону Кирх- гофа для контуров, образованных источником ЭДС, сопротивлением нагрузки и напряжением холостого хода между узлами 0′0 (рис. 6.6)

U a +U 0′0 −U A = 0, откуда U a = U A −U 0′0 .

Определение U a в последнем выражении возможно в случае, когда известно U ′0′0 – напряжение смещения нейтрали.

Напряжение смещения нейтрали можно определить по методу

двух узлов, представляя U

0′0

= ϕ

− ϕ или U

′

= ϕ′

при условии,

0′

0

0

0 0

что потенциал узла 0 принят равным нулю, тогда

U 0′0 = ϕ0′ =

E AY a + EBY a + EC Y c .

Y

a + Y b +

Y

c

Если по условию проектирования нулевой провод обладает некото- рой проводимостью, то последнее выражение можно переписать в

виде

90

U 0′0 = ϕ0′ =

E AY a + EBY a + EC Y c

.

Y a + Y b + Y c +

Y

0

A

a

IA

Ua

Za

Ia

EA

UА

U0/0

0

0'

Z b Ub

EC

EB

Uc

Z c

Ic

Ib

C

UC

UB

B

c

b

IC

IB

Рис. 6.6

При этом расчете было предположено, что сопротивления фазных обмоток генератора и сопротивления линейных проводов равны ну- лю. Если такие условия не соблюдаются, то эти сопротивления могут

быть учтены путем их введения в сопротивления соответствующих фаз Z a , Z b и Z c . При отсутствии сопротивлений обмоток генератора

их ЭДС равны фазным

+1

	U	CA = U ca					U A U a U AB
		+j				U	0′0	0'	U	b
			U	c				0
									U B
				U C

U BC = U bc

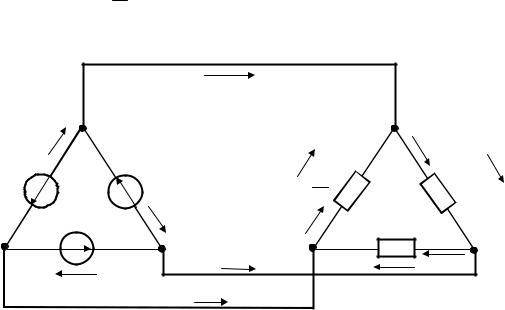
Рис. 6.7

напряжениям на

его зажимах E A =

U

A ,

EB =

U

B ,

EC = U C и

тогда полу-

ченную формулу

для

определения

смещения нейтрали можно записать

= U ab

для напряжений:

U 0′0 = U AY a +

U

B

Y

a +

U

C Y c .

Y a + Y b + Y c + Y 0

Напряжение

U0′0 называют

напряжением смещения нейтрали.

Векторная диаграмма для со- единения звезда-звезда без нулевого провода представлена на рис. 6.7.

91

= U AB , Z ab

= U BC , Z bc

= U AC . Z ac

6.5. Расчет соединения треугольник–треугольник

Пусть сопротивление фазных обмоток генератора и сопротивле- ния линейных проводов равны нулю (рис. 6.8), тогда U AB = U ab ,

U BC = U bc , U CA = U ca .
	Линейный провод
		IA		a
A
UCA			Uca	Iab	Uab
	EBA
EAC			Z аc		Z аb
ECB	UAB		Ica	Zbc
C	B	IB	c	Ibc	b
UBC		IC		Ubc

Рис. 6.8

Ток в фазах нагрузки – фазный ток:

I ab = U ab

Z ab

I bc = U bc

Zbc

I = U ac

ac Z ac

Линейные токи в общем случае, т. е. для несимметричной на- грузки, можно определить по первому закону Кирхгофа:

I A = I ab − I ca , I B = I bc − I ab , I C = I ca − I bc .

92

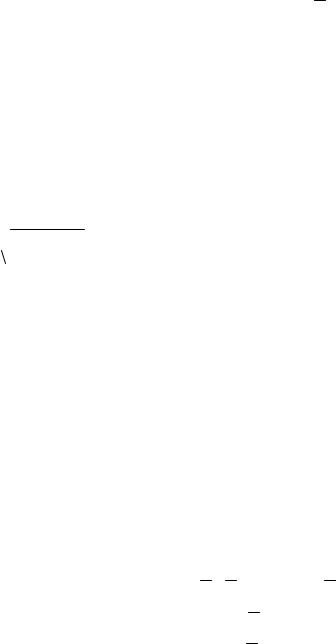
Для симметричной цепи линейные токи в 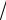3 раз больше фазных то- ков.

6.6.Активная, реактивная и полная мощности трёхфазной цепи

Под активной и реактивной мощностями трехфазной цепи по- нимают P = Pa + Pb + Pc + P0 и Q = Qa + Qb + Qc + Q0 . Полная мощ- ность S = P2 + Q2 .

Если нагрузка симметричная, то P0 = Q0 = 0,

Pa = Pb = Pc = UФIФ cosϕ, Qa = Qb = Qc = UФIФ sin ϕ,

и тогда мощность трёхфазной цепи может быть рассчитана через фазные токи и напряжения:

P = 3UФIФ cosϕ, Q = 3UФIФ sin ϕ,

S = 3UФIФ .

Активная, реактивная, полная мощности трехфазной цепи неза-

висимо от способа её соединения в звезду или треугольник могут быть найдены через линейные токи и напряжения:

S = 3UФIФ = 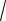3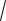3UФIФ = 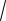3UЛIЛ ,

P = 3UФIФ cosϕ = 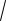3UЛ IЛсosϕ,

Q= 3UФIФ sin ϕ = 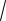3UЛIЛsinϕ .

6.7.Измерение активной мощностив трёхфазной цепи

Метод трёх ваттметров используют для измерения активной мощности трёхфазной цепи в случае несимметричной нагрузки. Ак- тивная мощность всей цепи равна сумме показаний всех ваттметров.

При симметричной нагрузке достаточно измерить мощность од- ной из фаз и результат утроить – метод одного ваттметра.

93

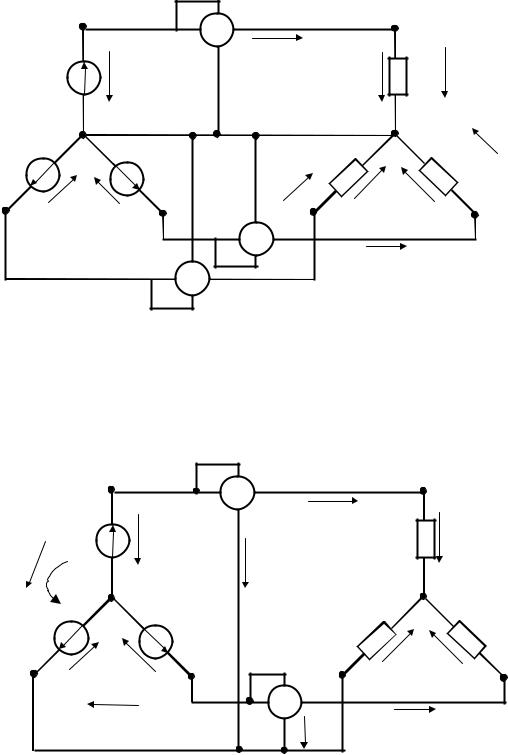
Схема измерения активной мощности трёхфазной цепи для не-
симметричной нагрузки показана на рис. 6.9.
	A	*		*			a
			Wa
	EA	UA		IA		Ua	Za		Ia
	0						0'		Ub
E		E			Z c				Z b
C		B		Uc
						Ic	Ib
C	UC	B			c				b
				* Wb
						IB
		Wc		*
		*	*
				Рис. 6.9
В случае, если узел 0′ недоступен, то измерение мощности можно
произвести двумя ваттметрами (рис. 6.10)
	A		*	*			a
				W1	IA
		UA					Z		Ia
	EA
UAC				UAC
	0							0'
	E	E				Z c			Z b
	C	B
C	UC	UB	B	*	c		Ic	Ib	b
		UBC		* W2	UBC		IB
				Рис. 6.10
94

Докажем, что сумма показаний двух ваттметров представляет

собой активную мощность трехфазной цепи

pW1 Þ Re{U AC I A} и

pW2 Þ Re{U BC I B .

Составим уравнение по второму закону Кирхгофа для контура, образованного фазными напряжениями UA и UС и линейным напря- жением UAC

	U AC +U C −U A = 0,
откуда	U AC = U A −	U	C ;
аналогично	U BC = U B −U C .

Определим полную комплексную мощность.

U AC I A + U BC I B = (U A - U C )I A + (U B - U C )I B = = U A I A -U C I A + U B I B - U C I B .

Учитывая, что	I A + I B + I C = 0
и	I C = −I A − I B ,

последнее выражение можно записать в виде

U A I A + U B I B + U C I C ,

что соответствует полной комплексной трехфазной цепи.

Сумма реальных частей каждого слагаемого соответствует ак- тивной мощности трехфазной цепи. Следовательно, активную мощ- ность трехфазной цепи можно измерить двумя ваттметрами. Такой

метод измерения активной мощности называют методом двух ваттметров.

95

Глава 7. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ НЕСИНУСОИДАЛЬНЫХПЕРИОДИЧЕСКИХ ЭДС,

НАПРЯЖЕНИЯХИ ТОКАХ

Во многих случаях при установившемся процессе кривые пе- риодических ЭДС, токов, напряжений в той или иной мере отличают- ся от синусоиды. Такие периодические несинусоидальные ЭДС, на- пряжения, токи можно представить в виде рядов Фурье, которые в общем случае содержат постоянную составляющую, основную гар- монику, имеющую период, равный периоду самой функции, и выс- шие гармоники, частота которых в целое число раз больше частоты основной гармоники.

Для линейных электрических цепей при периодических, несину- соидальных внешних воздействиях применим метод наложения. Ос- новываясь на нем, можно предложить следующий алгоритм расчета.

7.1. Алгоритм расчета

1. Заданное аналитическое выражение периодического несину- соидального напряжения (ЭДС, тока) раскладываем в ряд Фурье в

тригонометрической форме

n

u(t) = U0 + åUmk sin(kωt + ψuk ),

k =1

где k – номер гармоники.

2. Каждую гармонику напряжения (ЭДС, тока) записываем в

комплексной форме U mk = Umk e jΨuk .

3. Для каждой гармоники определяем (в зависимости от вы- бранного метода расчета) комплексное сопротивление или комплекс-

ную проводимость

	X Lk = kωL;						XCk =	1	;
								kωC
	B	Lk	=	1		;	B = kωС.
				kωL			Ck
	4. Для каждой гармоники напряжения (ЭДС, тока) находим
	комплексную амплитуду тока						I mk = Imk e jΨik .
	96

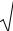
5. Записываем выражение для мгновенного значения тока для каждой гармоники в отдельности. Мгновенное значение периодиче- ского несинусоидального тока получают, суммируя мгновенные зна- чения всех гармонических составляющих токов:

i(t) = I0 + Im1 sin(ωt + Ψi1) + Im2 sin(2ωt + Ψi2 ) + Im3 sin(3ωt + Ψi3) +K,

n

i(t) = I0 + åImk sin(kωt + Ψik ).

k=1

7.2.Представление периодической несинусоидальной функцииввиде ряда Фурье

Любая периодическая несинусоидальная функция может быть представлена в виде ряда Фурье, если она удовлетворяет условиям Дирехле (функция должна иметь конечное число разрывов первого ряда и конечное число экстремумов). В реальных физических цепях таким условиям удовлетворяют все функции напряжения, ЭДС, тока:

u(t) = U0 +Um1 sin(ωt + Ψu1) +Um2 sin(2ωt + Ψu2 ) + ... + +Umk sin(kωt + Ψuk ),

где U0 – постоянная составляющая напряжения; Um1sin(ωt+ψ1k) – ос- новная (первая) гармоника; Umksin(kωt+ψuk) – высшая (k-я) гармоника; Emk – амплитуда k-й гармоники; ψk – начальная фаза k-й гармоники; kω – круговая частота k-й гармоники.

В общем случае ряд Фурье содержит бесконечное число членов,

но при расчете обычно ограничиваются некоторым конечным числом членов ряда, определяемым требуемой точностью расчета.

Для вычисления коэффициентов ряда Фурье целесообразно его члены представить через синусы и косинусы без начальных фаз:

U mksin(kωt + Ψk ) =U mkcosΨk sin kωt +U mksin Ψk coskωt = = Bk sin kωt + Ck coskωt,

∞

∞

u(t) = U0 + åBk sin kωt + åCk coskωt,

k =1

k =1

Ck

tg Ψ =

.

где B

k

=U

mk

cosΨ ;

C

k

=U

mk

sin Ψ ; U

mk

=

B2

+ C2

;

k

k

k

k

k

Bk

97

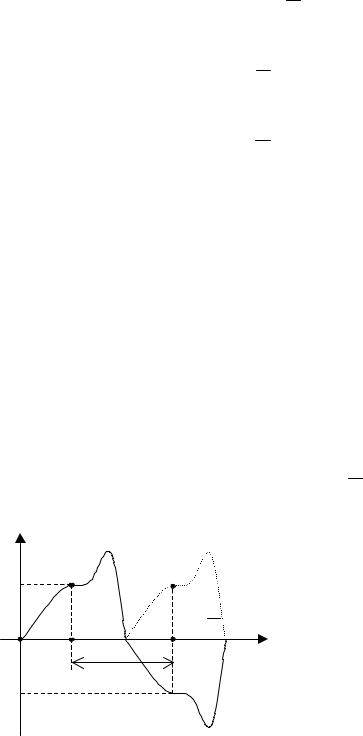
Постоянная составляющая U0 и коэффициенты Bk, Ck могут быть

определены из выражений

U0 = 1 Tòu(t)dt,

T 0

Bk = 2 Tòu(t)sin kωtdt, T 0

Ck = 2 Tòu(t)cos kωtdt. T 0

U0, Bk, Ck можно также определить из соответствующих графи- ков, используя формулы приближенного исчисления интегралов.

7.3. Гармонический состав кривой внекоторых случаях симметрии

7.3.1. Симметрия относительно оси абсцисс

График функции u(t) с симметрией относительно оси абсцисс представлен на рис. 7.1. Для такого случая симметрии справедливо

условие

			u(t) = −u(t + T ) .
			2
u			Ряд не содержит четных гар-
u			моник так как для них не удовле-
		T	творяется вышеприведенное усло-
t1	t1+		вие Bk = Ck =0 при k= 2,4,6… . Лю-
	T/2	2	t бая симметричная относительно
0			оси абсцисс кривая содержит толь-
–u			ко нечетные гармоники
			n
			u(t) = åUmk sin(kωt + Ψuk ),
	Рис. 7.1		k =1
			где U0=0, k= 1,3,5,7.
98

7.3.2. Симметрия относительно оси ординат

График функции u(t) с симметрией относительно оси ординат представлен на рис. 7.2. Для такого случая симметрии справедливо

условие

	u		u(t)=u(-t).
			B1 = B2 = B3 = … = Bk = 0.
	u		u(t)=U0+C1 cos ωt + C2 cos2ωt+
t1	t1	U0	+ Ck cos kωt,
		t	n
			u(t) = U0 + åCmk coskωt,
			k =1
	Рис. 7.2		где k= 1,2,3, ….

7.3.3. Симметрия относительно начала координат
			График функции u(t) с симметрией
	u		относительно начала координат	представ-
	u		лен на рис. 7.3. Для такого случая симмет-
			рии справедливо условие
-t1	t1	t	u(t)=–u(–t).
	-u		U0 = C1 = C2 = C3 = … = Ck = 0.
			∞
	Рис. 7.3		u(t) = åBmk sin kωt,
			k =1
			где k= 1,2,3,… .

7.4.Зависимость формы кривой тока от характера цепи при несинусоидальном напряжении

Сопротивление электрической цепи, содержащей индуктивные катушки и конденсаторы, зависит от частоты и, следовательно, ока- зывается различным для разных гармоник. Поэтому если к зажимам такой цепи приложено периодическое несинусоидальное напряжение, то кривая тока в цепи отличается по форме от кривой напряжения.

99