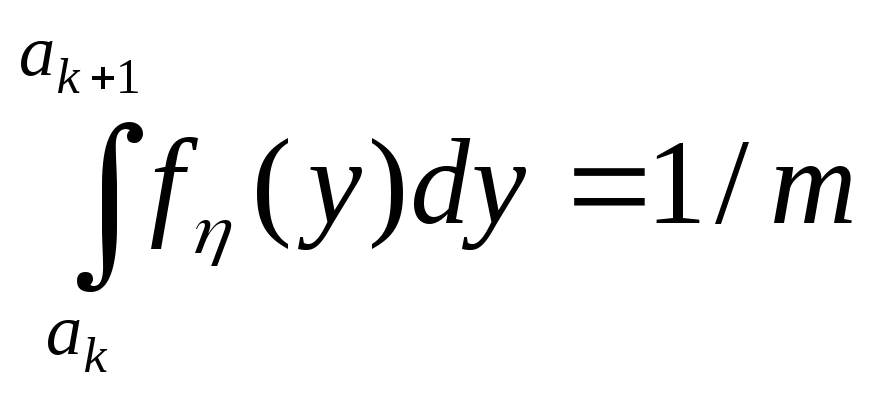15-25

17. Организация цифрового статистического моделирования; метод статистических испытаний (Монте-Карло). Метод статистических испытаний (Монте-Карло) базируется на иссл-ии случайных чисел, т.е. возможных значений нек. с.в. с заданным распределением вероятностей. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе. Статистические данные обрабатываются и классифицируются с использованием методов мат. статистики. Сущность метода: построение для процесса функционирования системы S некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды E, и реализация этого алгоритма с использованием программно-технических средств ЭВМ. Области применения: для изучения стохастических систем; для решения детерминированных задач. В результате статистического моделирования системы S получается серия частных значений искомых величин и функций, статистическая обработка которых позволяет получить сведения о реальном поведении системы в произвольные моменты времени. Если количество реализаций N достаточно велико, то полученные результаты моделирования системы приобретают статистическую устойчивость и с достаточной точностью могут быть приняты в качестве оценок искомых характеристик процесса функционирования системы S. Метод статистических испытаний (МСИ) — это специфич. инструмент для получения с.в., процессов и функций. Если этот метод включен в состав имитационной модели то она получает название имитационно-статистич. модели. В МСИ для реализации множества с.в. используются некоторые БСВ. В качестве БСВ можно взять любую, однако на практике принято использовать БСВ с равномерным распределением.	19. Способы формирования базовых случайных величин (БСВ); их возможности. Есть три способа получения с.в.: - аппаратный способ основан на использовании физических процессов, которые представлены как случайные (пр.: шумы в п/п приборах). Используется электронная приставка, на выходе которой формируется случайная функция. Недостаток метода: необходимость периодической настройки и невозможность повторного воспроизведения той же самой цепочки с.в. - табличный способ удобен когда требуется небольшое число с.в., которые предварительно д.б. получены и зафиксированы в ОЗУ. - алгоритмический способ используется чаще всего, т.к. не требует периодической настройки и специальных устройств для получения чисел, легко воспроизводится та же послед-ть, размер выборки задается разработчиком. В основе лежит специальный алгоритм, который при очередном обращении формирует только одну реализацию с.в., многократное обращение формирует заданное число реализаций. Все перечисленные способы позволяют реализовать только псевдослучайные величины (ПСВ). Такие алгоритмы строятся обычно с помощью рекуррентных процедур. xi+1=Ф(xi) – рекуррентное соотношение первого порядка. В качестве функции-генератора следует использовать функцию, плотно заполняющую квадрат (1,1). Необходимые требования для генерации БСВ: ПСВ д.б. независимы, неповторяющимися достаточно длительное время, воспроизводимыми, время генерации д.б. минимальным	20. Метод серединных квадратов для генерации БСВ. Один из первых м-дов получения последовательностей ПСВ. Пусть имеется 2n-разрядное число, меньшее 1: xi=0, a1 a2 … a2n. Возведем его в квадрат: xi^2=0, b1 b2 … b4n, а затем отберем средние 2n разрядов xi+1=0, bn+1 bn+2 … b3n, которые и будут являться очередным числом псевдослучайной последовательности. Недостаток этого метода – наличие корреляции между числами последовательности, а в некоторых случаях случайность вообще может отсутствовать (x0=0,4500, x0^2=0,20250000, x1=0,2500, x1^2=0,06250000, x2=0,2500 и т.д.) Кроме того, при некоторых i^* вообще может наблюдаться вырождение последовательности, т.е. xi=0 при i≥i^*. Это существенно ограничивает возможности использования метода серединных квадратов.
21. Свойство конгруэнтности (сравнимости) целочисленных величин и его использование в генераторах БСВ. Обычно для построения БСВ используются т.н. конгруэнтные процедуры. В основе этих методов лежит фундаментальное понятие о конгруэнтных величинах. Свойства конгруэнтности: 1) А и В целые числа; 2) интервал между числами А и В д.б. равен целому числу умноженному на m; 3) остатки от деления А и В на модуль m д.б. одинаковы. Формально: a,b,m – целые числа │a-b│ =k*m, где k – целое. ]a/m[=]b/m[ Если 1, 2, 3 выполн., то a=b(mod m) {т.е. сравнимы по модулю}. При формировании БСВ конгруэнтными процедурами, на роль очередных xi+1 и текущих xi выбираются конгруэнтные: xi+1=xi(mod m). Конгруэнтные процедуры являются чисто детерминированными, т.к. описываются виде рекуррентного соотношения, когда функция xi+1=Ф(xi) имеет вид xi+1≡αxi +β (mod m) xi= [α^ix0 + β (α^i-1) /(α-1)](mod m). Если задано начальное значение x0, множитель α и аддитивная константа β, то данная формула однозначно определяет послед-ть целых чисел {xi}.	22. Мультипликативная и мультипликативно-аддитивная процедура генерации БСВ. Конгруэнтная процедура получения послед-тей псевдослучайных чисел м.б. реализована мультипликативным либо мультипликативно-аддитивным методом. Мультипликативный метод задает послед-ть неотр. целых чисел {xi}, не превосходящих m, по формуле xi+1≡λxi(mod m). Получаются воспроизводимые последовательности. Требуемый объем памяти минимален, необходим последовательный подсчет произв-я двух целых чисел, т.е. вып-я операции, быстро реализуемой на ЭВМ. Для машинной реализации наиболее удобна версия m=p^g, где p – число цифр в системе счисления, принятой в ЭВМ, g – число бит в машинном слове. Тогда вычисление остатка от деления на m сводится к выделению g младших разрядов делимого, а преобразования целого числа xi в рациональную дробь из интервала (0,1) осуществляется подстановкой слева двоичной или десятичной запятой. Пример: для g=4, получить числа последовательности, используя алгоритм мультипликативного метода. выбираем x0=7(10)=0111(2) при t=1 получим λ=11(10) или 5(10) (λ=8t±3), пусть λ=5(10)=0101(2) рассчит. произв-е λx0, берем g мл. р-дов, вычисляем x1 и присваиваем x0=x1 λx0=(0101)(0111)=00100011, x1=0011, x1=3/16=0,1875 λx1=(0101)(0011)=00001111, x2=1111, x2=15/16=0,9375 и т.д. Мультипликативно-аддитивный м-д (смешанный) позв. вычислять послед-ть по формуле xi+1≡λxi +β (mod m), т.е. в отличие от мультиплик-ного м-да β≠0. Этот метод сложнее мультиплик-ного на одну операцию «+», но возможность выбора доп. параметра позволяет уменьшить корреляцию получаемых чисел.	24. Проверка БСВ; плотность распределения и математическое ожидание равномерного распределения. Эффективность статистического моделирования систем и достоверность получаемых результатов существенно зависит от БСВ. Проверка равномерности БСВ осуществляется следующим образом: Выдвигается гипотеза о равномерности распределения чисел в интервале (0,1). Затем интервал (0,1) разбивают на m равных частей, тогда при генерации последовательности {xi} каждое из чисел xi с вероятностью pj=1/m, j=1…m попадает в один из подинтервалов. Всего в каждый j-й интервал попадет Nj чисел. Относительная частота попадания случайных чисел в каждый подинтервал равна Nj/N. По виду полученной гистограммы и теоретической прямой можно судить о равномерности распределения БСВ. Плотность распределения – такая функция p(x)≥0, что вероятность неравенства a<x<b при любых a и b равна ∫a^b p(x)dx, при этом функция p(x) должна удовлетворять условию ∫p(x)dx=1. Математическое ожидание – среднее значение, одна из важнейших характеристик распределения вероятностей с.в. Плотность распределения равномерно распределенной с.в. на инт. (a,b) — это прямая f=1/(b-a). Мат. ожидание такой величины mx = (a+b)/2
23. Моделирование случайных событий и их описание. Пусть событие А происходит с вероятностью р(А). Соответственно противоположное событие А формируется с вероятностью 1-р(А). Появление любого из этих событий – достоверное событие, т.е. вероятность появления любого – равна 1. На оси абсцисс получаем пороговое значение с.в., а заштрихованная площадь соответственно есть ее значение. Процедура генерации: если xi<xпор, то событие А, иначе А, и формируем следующее xi+1, сравниваем с xпор. Аналогично формируем несколько случайных событий с заданными вероятностями: р(А1), р(А2) …. Для этого весь прямоугольник разбивается на несколько частей в соответствии с вероятностями. Если xi<x<xi+1 тогда Аi.	23. Моделирование непрерывных случайных величин методом обратной функции; способы их описания f(x) – дифференциальный закон распределения с.в. или плотность вероятности F(x) – интегральный закон распределения с.в. или функция распределения Непрерывная с.в. η задана интегральной функцией распределения: Fη(y)=P(η≤y)= Взаимно однозначная монотонная функция η=Fη^-1(ζ), полученная решением относительно η уравнения ζ=Fη(η), преобразует равномерно распределенную на интервале (0,1) величину ζ в η с требуемой плотностью fη(y) Если с.в. η имеет плотность распределения fη(y), то распределение с.в. ζ=. На основании этого можно сделать вывод: чтобы получить число, принадлежащее последовательности случайных чисел {yi}, имеющих функцию плотности fη(y), необходимо разрешить относительно yi уравнение	26. Моделирование дискретных случайных величин методом обратной функции; способы их описания. Дискретная с.в. η принимает значения y1≤y2≤…≤yi≤… с вероятностями р1, р2, …, составляющими дифференциальное распред-е вероятностей y y1 y2 … yi … Р(η=y) р1 р2 … рi … При этом интегральная функция распределения ym≤y≤ ym+1, m=1,2,…, Fη(y<y1)=0. Для получения дискретных с.в. можно использовать м-д обр. ф-ции. Если ζ – равномерно распределенная на интервале (0,1) с.в., то искомая с.в. η получается с помощью преобр-я η=Fη^-1(ζ), где Fη^-1 – ф-ция, обратная Fη. Алгоритм вычисления сводится к выполнению следующих действий: если x1<p1 то η=y1, иначе, если x2<p1+p2 то η=y2, иначе … , если то η=ym, иначе …
28. Универсальный способ формирования непрерывной случайной величины. Основан на кусочной аппроксимации ф-ции плотности. Пусть требуется получить послед-ть случайных чисел {yi} с ф-цией плотности fη(y) на интервале (a,b). Представим fη(y) в виде кусочно-постоянной ф-ции, т.е. разобьем интервал (a,b) на m интервалов, и будем считать fη(y) на каждом интервале постоянной, тогда с.в. можно представить в виде η=ak+ηk^*, где ak – абсцисса левой границы k-го интервала, ηk^*- с.в., возможные значения которой располагаются равномерно внутри k-го интервала, т.е. на каждом участке ak÷ak+1 величина ηk^* считается распределенной равномерно. Чтобы аппроксимировать fη(y) наиболее удобным способом, целесообразно разбить (a,b) на интервалы так, чтобы вероятность попадания с.в. η в любой интервал (ak,ak+1) была постоянной, т.е. не зависела от номера интервала. Таким образом, для вычисления аk воспользуемся следующим соотношением Достоинства: при реализации на ЭВМ требуется небольшое кол-во операций Алгоритм машинной реализации: генерируется БСВ с помощью БСВ выбирается случайный интервал (ak,ak+1) генерируется число xi+1 и масштабируется с целью приведения его к интервалу (ak,ak+1) т.е. домножается на коэффициент (ak+1-ak) xi+1 выявляется случ. число yj=ak+(ak+1-ak) xi+1 с требуемым з-ном распред-я	25. Проверка законов распределения ПСВ; критерий Пирсона. Пусть имеется теор. закон распределения с.в. Имеется некоторое мн-во статистических данных, которые подчиняются некоторому собственному закону распред-я. Фактические данные могут отличаться от теории в связи с тем, что: а) теор. кривая не соотв. фактическому распределению, т.е. гипотеза не верна; б) случайные факторы. При условии, что гипотеза выбрана правильно, мы должны убедиться, что отклонения полученной кривой от теор. связаны со случ. факторами. Для этого определяем вероятность того, что зафиксированное случайное расхождение не больше допустимого и объясняется случ. факторами. Для опред-я расхождения теор. кривой с практической разбиваем весь диапазон на интервалы, при этом чем больше выборка тем точнее. Подсчитываем число попаданий в каждый интервал Ni, и статистическую вероятность Ni/N. Сама мера или степень расхождения является с.в. и подчинена своему з-ну распред-я, зависящему от вида теор. кривой и случайных факторов. Для проверки закона распределения используют критерий Пирсона. Идея м-да сост. в контроле отклонения гистограммы эксперим. данных от теор. Распред-е χ^2 зависит не только от кол-ва интервалов, но и от числа степеней свободы r, которые определяются во-первых числом интервалов, а во-вторых числом независимых условий и связей: r=k-s, s определяется кол-вом ограничений, накладываемых на фактич. распред-е. По спец. таблицам определяем вер-ть того, что факт. расхождение будет не меньше полученного в связи с чисто случайными факторами.