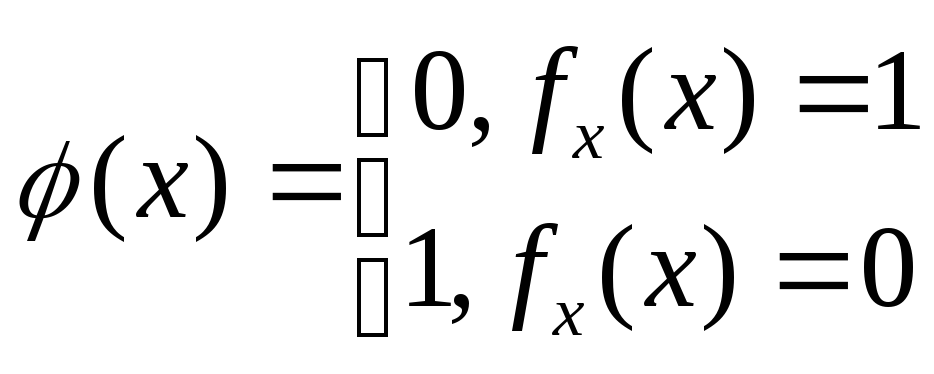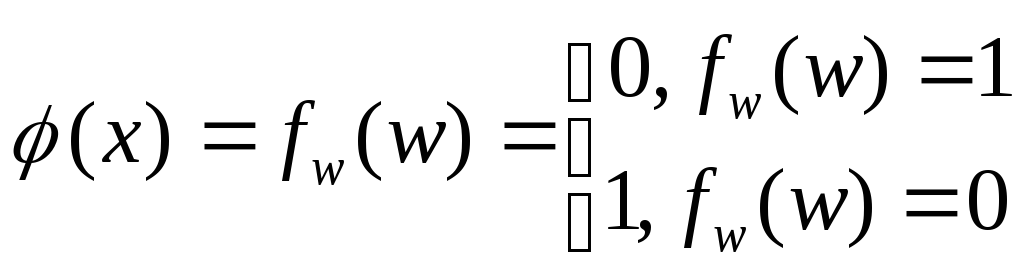Шпоры, 1ый семестр [3030 вопросов]
.doc|
1. Введение в предмет - алгоритм - 3 знаменитых задачи - квадратура круга - угол на 3 равных - задача Диофанта - идея универсального алгоритма – Лейбниц - теория множест – Кантор, Фреге, Гильберт - Гёдель доказал несуществование универсального алгоритма - Тьюринг - основные задачи теории алгоритмов - можно ли создать алгоритм для данной задачи - оценить его вычислительную сложность |
2. Понятие машины Тьюринга - состоит из - устройство управления - головка для чтения/записи - бесконечная лента, разбитая на ячейки - МТ – универсальное вычислительное устройство - входной алфавит - пример - конфигурация - содержимое ленты вместе с состоянием машины - вычисление - последовательность конфигураций - детерминированная – нет повторов в левой части - арифмитическая МТ – если на ленте цифры
|
- тезис Тьюринга – МТ можно считать вычислимой арифметической функцией и наоборот - функция – отображение одного множества чисел в другое - распознающая МТ – обладает ли входное свойством 3. Представление машины Тьюринга - таблица - диаграмма 4. Альтернативы машине Тьюринга - машина Поста - нормальный алгоритм Маркова (замена) - персептрон (нервн. клетка)
|
-
МТ равносильна М. Маркова.
5. Нумерация машин Тьюринга - каждый алгоритм, программа, вычислимая функция, МТ имеет номер (Гёделя) 6. Невычислимые функции - диагонализационный метод Кантора
|
|
7. Примеры алгоритмически неразрешимых проблем - для вычислимой ф-ции можно составить правило для вычисления обратной функции - неразрешимые проблемы: самоприменимость и вычислимость 8. Современное программирование с точки зрения машины Тьюринга - 4 основных оператора - любой язык программирования универсален 9. Рекурсивные функции и множества - примитивные рекурсивные функции: - f(x)=c константа - f(x)=x+1 сложение с единицей - f(x , x , x ,..., x )=x проекции |
- сложные из простых с помощью операторов - подстановка - рекурсия - минимизация - частично-рекурсивные: D(y)!=R - тезис Черча: всякая вычислимая функция – частично-рекурсивная -мн-во можно задать: -перечислением эл-ов - указанием свойств эл-ов, тогда это множество рекурсивное, а формула – характеристическая функция мн-ва - рекурсивно-перечислимое мн-во – если D(y)!=R - дополнение мн-ва – мн-во, не содержащее эл-ов данного |
10. Операция примитивной рекурсии - пример: операция факториала - все вычислимые функции строятся из простейших ф-ций и операторов 11. Графическое и схемное описание алгоритмов - дерево состояний (лифт) - оптимизация блок-схем: уменьшить количество вершин и логических условий - избыточное логическое условие – если его можно определить из других 12. Табличный способ представления алгоритмов - пример: нахождение НОД
|
13. Уменьшение числа состояний -состояния: - 0-различимые – M={S , S } и N={S , S ,..., S } - 1-различимые – под действием одинаковых условий переходят оба в M или N 14. Алгоритмы и исчисления - исчисление соответствует недетерминированной МТ, а алгоритм – детерминированной - всякое исчисление эквивалентно какому-то алгоритму и наоборот - пример распознающей МТ (число или нет) – дет. - пример расп. МТ (города) – недетрминирован. |
|
15. Информационная сложность (энтропия) - энтропия (оценивает информационную сложность) – для оценки ..... хаотичности движения молекул газов - информационная слож-сть – макс. кол-во однонаправл. путей, проходящих через сечение -
- алг-кий способ вычисления слож-сти – длина (кол-во символов, байт) программы - вывод: -не сущ-ет алг-ма, который для любой задачи устанавливал бы наименьшую длину программы для ее решения - маленькие программы могут содержать информации на много порядков > чем большие |
16. Вычислительная сложность -оценки сложности: - временная (опр-ся кол-ом тактов (этераций) МТ ) - затраты памяти - полимиальный алгоритмы – хороший алгоритм 17. Классы P и NP - P – класс задач, решаемых с пом. полимиальных детерминированных МТ - NP – недетрминированных полимиальных МТ 18. Понятие о полной задаче - полная задача – если к ней можно свести любую задачу из этого класса - полиномиально полная – если можно за полиномиальное время |
19. Задача ВЫПОЛНИМОСТЬ - она NP-полная задача - дизъюнкция - она логическая, проверяет имеет ли мн-во дизъюнктов хотя бы одно решение 20. Задаче о раскраске графа -три цвета 23. Теорема Кука (общий подход) -Th: ВЫПОЛНИМОСТЬ явл-ся полной в классе NP 24. Задача о покрытии -строка покрывает столбец, если содержит в нём единицу - покрытие матрицы – любое мн-во строк, что каждый столбец матрицы покрывается хотя бы одной строкой
|
29. Использование слабых методов и эвристик -слабый – простой в вычислении, но не факт, что правильный или оптимальный - после применения нужно менять траекторию - эвристика – совокупность методов поиска решений задач 30. Жадные алгоритмы на матроидах - жадный пример: расписание (свободному максимальную работу), макс. отклонение 11% - если на матроидах, то всегда оптимален - дерево – граф без контуров и петель - остовное дерево – если есть путь из любой вершины в любую - матроид – мн-во независимых множеств
|
|
1. Введение в предмет. Решение задач – основной вид человеческой деятельности. Задачи решают с помощью алгоритмов. Алгоритм – некоторое строгое предписание действий при выполнении кот. Достигается заявляемый результат. Слово алгоритм происходит от имени узбекского ученого Аль Хорезма, кот. Разработал систему правил для решения квадратных уравнений. «Три знаменитые задачи»: задача о квадратуре круга, трисекция угла, задача Диофанта. Лейбниц предложил идею универсального алгоритма. Кантор, Фреге, Гильберт заложили основу теории алгоритмов. Созданием теории множеств Гильберт выдвинул ряд проблем: разработать универсальный алгоритм для проведения доказательства. 1935 г. – Гедель доказал, что такой алгоритм создать невозможно. 1940 г. – Тьюринг сформулировал точное математически строгое определение алгоритма. Он придумал простейшую вычислительную схему. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ АЛГОРИТМОВ: 1. Выяснить, можно ли простроить алгоритм для данной задачи. 2. Оценить его вычислительную сложность. |
2. Понятие МТ.
Имеется бесконечная
лента, разбитая на ячейки. В каждой
ячейке может быть записан 1 символ.
У-У управляет движением ленты. на
каждом шаге лента может сдвигаться в
люб. Сторону на одну клетку, либо
оставаться на месте. Принцип работы:
считывается текущий символ из ячейки,
просматриваемой головкой и далее УУ
производит сдвиг ленты и переходит в
некоторое состояние из конечного
множества состояний. И так до тех пор,
пока машина не попадает в конечное
состояние. МТ позволяет выполнить
определенные преобразования содержимого
ленты. МТ - Универсальное вычислительное
устройство. Под входным алфавитом МТ
понимают конечный набор символов,
который может быть на ленте. Одним из
простейших «1,0». Т.е. получаем 2-ичные
слова. Дополнительно используется
символ
|
3. Представление МТ. Каждое правило МТ можно схематически представить следующим образом:
Если машина
находится в состоянии S(i)
и текущий символ, просматриваемый
головкой -
То, что находится на ленте в момент окончания работы называется ответом. Содержимое ленты вместе с состоянием машины называется конфигурацией. Последовательность конфигураций – вычисление. МТ называется детерминированной, если нет 2-х и более правил с одинаковой левой, на разными правыми частями. МТ называется арифметической, если на ленте записаны числа. В этом случае говорят, что МТ вычисляет некоторую арифметическую функцию. Тезис Тьюринга: МТ равносильна вычислимой арифметической функции. Функция невычислима, если для нее нет МТ, т.е. нет алгоритма вычисления. Наиболее простой способ представления МТ – представление с помощью таблицы. 2-й способ – через диаграмму состояний. |
4. Альтернативы МТ Альтернативой МТ является машина Поста и алгоритм Маркова. Правило машин Маркова моэно проиллюстрировать на примере 1) ab ->cd, 2) ba->dc. Если во входном слове встречается комбинация ab, то в результате применения правила 1 она меняется на cd. МТ равносильна М. Маркова. Докажем. Рассмотрим 1 правило.
Для представления равносильного правила Маркова введем 2 новых обозначения T,Q – произвольный комбинации символов; x – произвольный символ. Запишем следующее правило Маркова:
Применив к (*) (**) получим
В 50-х гг. изобрели схему Персептрона, которая напоминает работу нервной клетки. Персептрон работает как распознающее устройство. От выбора коэффициента зависит правильная работа машины, поэтому их выбор – основная задача. |
|
5. Нумерация МТ. Каждая МТ имеет свой уникальный номер. Преобразовать последовательность символов в номер. Каждая буква имеет определенный номер в алфавите. 19, 28, 28, 37, 19, 29, 27, 12, 38 (номер Гёделя) Воспользуемся основной теоремой арифметики: каждое число можно разложить на простые множители единственным образом.
Вывод: каждая вычислимая функция имеет номер. Каждая программа имеет номер. Каждый алгоритм имеет номер. По номеру можно восстановить программу(алгоритм, функцию). Количество алгоритмов является счетным.
|
6. Невычислимые функции. Функция является невычислимой, если для нее нет МТ (алгоритма), т.е. ее можно только описать, а алгоритм вычисления задать нельзя. Большую роль в доказательстве играет роль диагональный метод Кантора. Составим таблицу. В ячейках – значения функций. Определим новую функцию:
Данная функция принимает значения по диагонали таблицы. ТЕОРЕМА.
Функция
|
7. Примеры алгоритмически неразрешимых проблем. Имеется 2 знаменитые неразрешимые проблемы: проблема само(не)применимости, проблема остановки. Доказательство каждой основано на получении противоречий. Проблема самоприменимости.
Построим
функцию
Для
функции
Предположим,
что функция
|
Таким
образом, получив противоречие, мы
понимаем что функция
Поэтому нельзя определить, самоприменима она или нет. Проблема остановки. Требуется установить для любой вычислимой функции, сходится она или нет. |
|
|
|
|
|
|
|
|
(*),
введем 2 новых обозначения T,Q
– произвольные комбинации символов;
x
– произвольный символ. Правило Маркова:
(**)
Применив к (*) (**) получим
- оценивает сложность системы: р –
вероятность состояния S
,
обозначающий пустую ячейку.
,
то машина переходит в состоянии S(k),
записывает символ
и производит сдвиг ленты А. А=(L,R,S).
Если машина стирает символ, это можно
передать как запись пустого символа.
(*)
(**)
является невычислимой. (для нее нет
МТ и номера Гёделя)
x
- номер МТ, вычисляющий данную функцию.
Данная функция вычисляет значение на
собственном номере.
нет МТ.
вычислима. Значит существует
невычислимая…