
Учебные материалы (Практические занятия, контрольные задания, конспект лекций) / Практические занятия / Практическое занятие 5
.docПрактическое занятие №5. Примеры NP-полных задач.
Цель занятия.
Целью данного занятия является ознакомление с основными NP-полными задачами..
Краткие теоретические сведения.
Напомним, что задача является NP-полной, если к ней можно эффективно свести задачу ВЫПОЛНИМОСТЬ, NP-полноту которой доказал С.Кук.
Имеет место ряд важных практических задач, для которых установлена их NP-полнота.
ЗАДАЧА ВЕРШИННОЕ ПОКРЫТИЕ.
Графом называется множество вершин и связывающих их ребер. Пример графа дает рис.1.
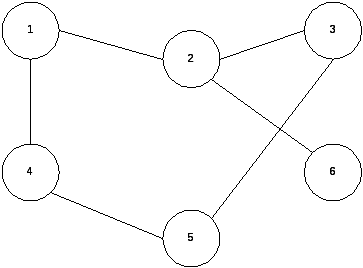
Вершины представлены с помощью кружков. Номера вершин указаны числами внутри кружков. Ребра – отрезки прямых линий, соединяющие вершины.
Будем говорить, что вершина i покрывает некоторое ребро, если данная вершина i является концевой вершиной рассматриваемого ребра.
Множество вершин называется вершинным покрытием, если для каждого ребра графа найдется хотя бы одна вершина из , которая ее покрывает. Так, одним из возможных вершинных покрытий представленного выше графа, является ={2,4,5}.
Задача ВЕРШИННОЕ ПОКРЫТИЕ требует найти покрытие с заданным числом вершин.
Задание 1. Показать, что задача – найти вершинное покрытие минимального размера также NP-полна.
Закодируем граф с помощью матрицы смежности M вершин

|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
2 |
1 |
0 |
1 |
0 |
0 |
1 |
|
3 |
0 |
1 |
0 |
0 |
1 |
0 |
|
4 |
1 |
0 |
0 |
0 |
1 |
0 |
|
5 |
0 |
0 |
1 |
1 |
0 |
0 |
|
6 |
0 |
1 |
0 |
0 |
0 |
0 |
Для экономии, часто в матрице смежности указывают только 1, а 0 – нет. Как видим, матрица смежности квадратная и симметричная.
Вопрос. Чему же соответствует вершинное покрытие размером, скажем, 3 на этой матрице?
Ответ: оно соответствует нулевой квадратной подматрице с одноименными строками и столбцами, размером 3*3.
ЗАДАЧА о КЛИКЕ размером n.
Эта задача состоит в том, чтобы для произвольного графа определить n вершин, никакие две из которых не соединены ребром. Так, примером клики размером 3 для изображенного выше графа является следующий: {1,5,6}.
Задание 2 . Найдите какую-нибудь другую клику размером 3.
Ответ: {3,4,6}.
Задание 3. Придумайте какой-нибудь собственный метод отыскания максимальной клики (т.е. клики максимального размера).
Задание 4. Доказать, что если - минимальное вершинное покрытие данного графа, то все вершины, не вошедшие в , образуют максимальную клику этого графа.
Так, клика {1,5,6} максимальная. Следовательно, множество {2,3,4} – есть минимальное вершинное покрытие.
Доказательство. Пусть В – множество вершин и Е – множество ребер графа и К –максимальная клика. Нужно показать, что разность В\К есть минимальное покрытие. Допустим, что это не так. Скажем, вершина х принадлежит действительно минимальному покрытию и не попала в В\К. Включим ее в В\К . Тогда она “выбьет” из В\К скажем вершины z,w как лишние (избыточные). Эти вершины z,w покрывают какие-то ребра. Но тогда и вершина х должна покрывать эти же ребра. Кроме того, ясно, что нет ребра (z,w). (Почему ?). Приходим к простому выводу, что вершина х должна быть концевой для всех таких ребер, другими концами которых являются z,w . Следовательно, вершины z,w могут быть включены в максимальную клику.
ЗАДАЧА о Гамильтоновом цикле.
Спрашивается, имеется ли в графе путь, проходящий через каждую вершину ровно один раз, который бы завершался в той же вершине, из которой он стартует.
