Добавил:

Kaz Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

Математические модели информационных процессов и управления

Файл:

Практическое занятие №10

.doc

Скачиваний:

Добавлен:

15.06.2014

Размер:

182.78 Кб

Скачать

☆

Практическое занятие №10

ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ НАЙКВИСТА И МИХАЙЛОВА

Критерий Найквиста предложен Найквистом в 1932-м году для усилителей с обратной связью. С конца 30–х годов является наиболее употребительным критерием устойчивости. Он позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы. Таким образом, тот факт, что система автоматического управления, как правило, является системой с обратной связью, учитывается с самого начала. Несмотря на то, что во всех формулировках фигурируют частные характеристики разомкнутых систем, условия устойчивости относятся именно к замкнутым, т.е. к результату замыкания той системы, частотные характеристики которой рассматриваются. Под замыканием понимается подсоединение выхода разомкнутой системы (через единичную обратную связь) к сравнивающему звену. Если в системе с отрицательной обратной связью «разорвать» обратную связь и считать выходным сигналом то, что до разрыва шло на звено сравнения, то получим разомкнутую систему.

На первый взгляд кажется, что в этом кроется определённое неудобство, но на самом деле возможность судить об устойчивости замкнутой системы по частотной характеристике разомкнутой является большим достоинством. Действительно, чаще всего проектировщик компонует прямую и обратную ветви замкнутой системы из сравнительно простых и известных составляющих в виде последовательного соединения звеньев, а затем соединяет их по схеме обратной связи. Передаточная функция последовательного соединения звеньев очень просто вычисляется, нередко, вплоть до значений корней характеристического уравнения. Суждение об устойчивости разомкнутой системы в этой ситуации не представляет труда, чего нельзя сказать о замкнутой системе.

Таким образом, основными достоинствами критерия Найквиста, являются:

– он основан на использовании п.ф. разомкнутой системы W(s), что облегчает построение частотных характеристик и упрощает анализ устойчивости путём применения логарифмических частотных характеристик;

– исследование устойчивости замкнутой системы сводится к анализу её свойств в разомкнутом состоянии, что облегчает процедуру процедуры синтеза, предоставляя возможность разработчику необходимым образом менять W(s);

– возможно использование для анализа устойчивости частотных характеристик системы, полученных экспериментально.

Опуская вывод критерия Найквиста, который базируется на принципе аргумента, рассмотрим формулировки критерия Найквиста для следующих частных случаев, приведя потом общую формулировку критерия:

– система в разомкнутом состоянии устойчива;

– система в разомкнутом состоянии неустойчива;

– система в разомкнутом состоянии находится на границе устойчивости.

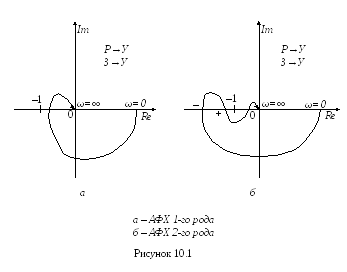
Для того, чтобы система, устойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении частоты ω от 0 до +∞ не охватывала точку (-1;j0) (рисунок 10.1).

Различают АФХ 1-го и 2-го родов. АФХ 1-го рода пересекает ось абсцисс справа от точки (–1;j0) (см. рисунок 10.1, а), а АФХ 2-го рода пересекает ось абсцисс и слева, и справа от точки (–1;j0) (см. рисунок 10.1, б).

В случае АФХ 2-го рода система в замкнутом состоянии будет устойчивой при условии, что при изменении частоты ω от 0 до +∞ разность между числом положительных (сверху вниз) и числом отрицательных (снизу вверх) переходов АФХ через ось абсцисс слева от точки (–1;j0) [т.е. через отрезок вещественной оси (–∞;–1)] равна нулю.

Для того, чтобы система, неустойчивая в разомкнутом состоянии, была устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы АФХ разомкнутой системы W(jω) при изменении ω от 0 до +∞ охватывала l/2 раз в положительном направлении точку (–1;j0), где l – число правых корней характеристического уравнения разомкнутой системы (рисунок 10.2).

Если характеристика W(jω) начинается на отрезке (–∞; –1) при ω=0 или заканчивается на нём при ω=+∞, то в этих случаях считают, что она совершает полперехода.

Критерий Найквиста распространяется также на случай астатических систем с порядком астатизма ν. Эти системы в разомкнутом состоянии находятся на границе устойчивости, так как их характеристическое уравнение имеет корень в начале координат кратности ν. В этом случае АФХ дополняют дугой –νπ/2 (в отрицательном направлении, т.е. по часовой стрелке) окружности бесконечно большого радиуса, начинающейся на положительной вещественной полуоси, после чего применяют критерий Найквиста в прежней формулировке. Приведём формулировку критерия Найквиста для случая, когда разомкнутая система находится на границе устойчивости.

Для устойчивости замкнутой САУ, которая в разомкнутом состоянии находится на границе устойчивости, имея нулевые корни характеристического уравнения, необходимо и достаточно, чтобы АФХ разомкнутой системы W(jω), дополненная дугой бесконечного радиуса, при изменении ω от 0 до +∞ не охватывала точку (–1;j0) (рисунок 10.3).

Общая формулировка критерия Найквиста охватывает все три рассмотренных выше случая.

Для устойчивости замкнутой САУ необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФХ разомкнутой системы W(jω) через отрезок вещественной оси (–∞;–1) была равна l/2, где – число правых характеристического уравнения разомкнутой системы. При этом угол поворота характеристического вектора замкнутой системы 1+W(jω) при возрастании ω от 0 до +∞ должен быть равен 2π(l/2) [или годограф охватывает точку (-1, j0) в положительном направлении l/2 раз].

Таким образом, при использовании критерия Найквиста, вообще говоря, необходимо убедиться в том, имеются ли в знаменателе передаточной функции разомкнутой системы корни, лежащие в правой полуплоскости, и сколько имеется таких корней.

Если АФХ разомкнутой системы проходит через критическую точку (-1, j0), то замкнутая система находится на границе устойчивости.

С ростом коэффициента усиления разомкнутой системы модуль АФХ также растёт, при этом фазовая характеристика не изменяется. Следовательно, при некотором значении коэффициента усиления K=K_кр, называемого критическим коэффициентом усиления, АФХ W(jω) пройдёт через точку (-1, j0), т.е. система будет на границе устойчивости. При K>K_кр система будет неустойчива.

Замкнутая система, которая остаётся устойчивой при безграничном увеличении коэффициента усиления разомкнутой системы, называется абсолютно устойчивой.

Если же с увеличением (или с уменьшением) коэффициента усиления система может потерять устойчивость, то система называется условно устойчивой. За исключением колебательного звена, все остальные системы условно устойчивы.

По соображениям повышения статической точности почти всегда стремятся сделать коэффициент усиления разомкнутой системы как можно больше. И это приводит к потере устойчивости. На рисунке 10.4, а показано, как годограф Найквиста системы [с передаточной функцией ], не охватывающий точку (-1, j0), при увеличении коэффициента усиления K в два раза [] стал охватывать её при бóльшем значении этого коэффициента K.

Однако встречаются системы (с внутренними обратными связями), в которых потеря устойчивости может произойти не только при увеличении коэффициента усиления, но также и при его уменьшении. Этим случаям могут соответствовать так называемые клювообразные АФХ (см. рисунок 10.4, б).

Для нормального функционирования система управления, кроме свойства устойчивости, должна обладать и некоторым запасом устойчивости. Дело в том, что в условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определённых пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.

Запасы устойчивости системы вводятся на основе частотного критерия Найквиста. Вполне очевидно, что чем дальше годограф находится от критической точки (-1, j0), тем, вероятно, система будет находиться дальше от границы устойчивости, будет «более устойчивой».

Числовые величины, характеризующие степень удаления АФХ разомкнутой системы от критической точки (-1, j0), носят название запасов устойчивости и могут быть введены различными способами. Различают запас устойчивости по амплитуде (модулю) ΔА и по фазе Δφ (рисунок 10.5).

Для определения запаса устойчивости по амплитуде достаточно определить значение амплитуды годографа при , под которой понимается такое значение частоты, при которой фазовая характеристика равна -, т.е. . Запас устойчивости по амплитуде ΔА – это величина

Рисунок 10.5 – Запасы устойчивости

отрезка оси абсцисс между критической точкой (-1, j0) и точкой пересечения годографа с осью абсцисс, т.е.

. (10.1)

Очевидно, что это определение имеет смысл, если ; тогда ΔА всегда меньше единицы. В противном случае годограф охватывает точку (-1, j0) и система неустойчива. Не будем пока рассматривать случай многократного пересечения годографом действительной оси. Пока только ясно, что речь идёт о ближайшем к критической точке пересечении годографом отрицательной части действительной оси справа от критической точки.

Для определения запаса устойчивости по фазе следует сначала определить значение фазы годографа при , под которой понимается такое значение частоты, при которой амплитудно-частотная характеристика равна 1, т.е. . Запас устойчивости по фазе Δφ фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется как разность

. (10.2)

Здесь также имеют смысл только положительные значения запаса устойчивости Δφ>0, так как в противном случае годограф Найквиста охватывает точку (-1, j0), поэтому замкнутая система неустойчива и говорить о запасе устойчивости не имеет смысла.

На рисунке 10.5 показаны запасы устойчивости и их связь с частотой среза _с и частотой _–_, при которой фазовая характеристика принимает значение -. На наш взгляд, геометрические представления введенных понятий более наглядны, чем приведенные формулы, если заметить, что окружность имеет единичный радиус.

C ростом коэффициента усиления разомкнутой системы модуль АФХ также растёт и при некотором значении коэффициента усиления K=K_кр, называемого критическим коэффициентом усиления, АФХ пройдёт через точку (-1, j0), т.е. система будет на границе устойчивости. При K>K_кр система будет неустойчивой.

Если характеристика имеет более сложные очертания, так называемая клювообразная, представленная на рисунке 10.6, а, то запас по амплитуде характеризуют двумя числами ΔА₁ и ΔА₂, а запас по фазе Δφ определяется обычным образом. Чтобы система обладала требуемым запасом устойчивости при заданных величинах ΔА и Δφ, около критической точки (-1, j0) вычерчивается некоторая запретная область в виде сектора, ограниченного величинами ±ΔА и ±Δφ, в которую не должна входить.

Критерий устойчивости Михайлова, сформулированный в 1938 году советским учёным А.В.Михайловым, является, по существу, геометрической интерпретацией принципа аргумента и позволяет судить об устойчивости системы на основании рассмотрения некоторой кривой, называемой кривой Михайлова.

Критерий Михайлова даёт возможность судить об устойчивости системы по годографу характеристического вектора системы D(jω)=D(s)|_s₌_jω, где

представляет собой левую часть характеристического уравнения системы. Если подставить в этот полином чисто мнимое значение s=jω, то получим комплексный полином

, (10.3)

где X(ω) и Y(ω) называют соответственно вещественной и мнимой функциями Михайлова.

При изменении частоты ω вектор D(jω), изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой (годографом) Михайлова.

Согласно критерию Михайлова для устойчивости САУ необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении ω от 0 до +∞, начинаясь при ω=0 на вещественной положительной полуоси, последовательно обходила в положительном направлении (против часовой стрелки) n квадрантов, где n – порядок характеристического уравнения, и при этом нигде не обращалась в ноль.

Кривая Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причём конец её уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического уравнения. На рисунке 10.7, а показаны типичные кривые Михайлова для устойчивых систем, описываемых уравнениями, начиная от первого (n=1) и кончая пятым (n=5) порядком; для удобства сравнения коэффициенты a₀ во всех случаях приняты одинаковыми.

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора D(jω) оказывается меньше, чем nπ/2. Если характеристическое уравнение n-го порядка имеет l правых корней, то при изменении ω от 0 до +∞ общий угол поворота характеристического вектора D(jω) будет

. (10.4)

Соотношение (10.4) справедливо только в том случае, если годограф Михайлова не проходит через начало координат.

На рисунке 10.7, б-ж показаны кривые Михайлова для неустойчивых и нейтральных систем. Рисунок 10.7, б – при ω=0 кривая Михайлова начинается на отрицательной вещественной полуоси; система неустойчива. Рисунок 10.7, в – порядок уравнения n=5, а кривая Михайлова находится вся в одном квадранте [этому соответствует характеристическое уравнение D(s)=a₅s⁵+a₄s⁴+a₀]; система неустойчива. Рисунок 10.7, г – нарушена последовательность прохождения квадрантов; система неустойчива. Рисунок 10.7, д – кривая Михайлова начинается в начале координат, т.е. в характеристическом уравнении имеется по крайней мере один нулевой корень; система находится на границе апериодической устойчивости; небольшая деформация кривой Михайлова (прерывистая линия) делает систему устойчивой. Рисунок 10.7, е – кривая Михайлова проходит при некотором значении ω_k через начало координат, т.е. в характеристическом уравнении имеются чисто мнимые корни ±jω_k; система находится на границе колебательной устойчивости; небольшая деформация кривой Михайлова делает систему устойчивой (прерывистая линия). Рисунок 10.7, ж – кривая Михайлова проходит через начало координат, но небольшой деформацией кривой Михайлова удовлетворить условиям устойчивости нельзя; система неустойчива.

Построение кривой Михайлова можно производить методом контрольных точек, который сводится к определению ряда точек кривой Михайлова, соответствующих фиксированным значениям частоты ω, включая обязательно частоты точек пересечения кривой с осями координат. Они (частоты) находятся как корни уравнений

X(ω)=0; (10.5)

Y(ω)=0. (10.6)

Анализируя годографы Михайлова, можно установить следующее следствие из критерия устойчивости Михайлова. При последовательном прохождении кривой Михайлова квадрантов координатной плоскости вещественная и мнимая оси пересекаются ею поочерёдно. В точках пересечения кривой Михайлова с вещественной осью обращается в нуль мнимая функция Михайлова Y(ω), а в точках пересечения кривой с мнимой осью обращается в нуль вещественная функция X(ω). Вещественную X(ω) и мнимую Y(ω) функции Михайлова можно представить графически в виде кривых (рисунок 10.8). Точки пересечения этих кривых с осью абсцисс дают значения корней уравнений (10.5) и (10.6).

Если обозначить корни уравнения (10.6) через ω₀, ω₂, ω₄, …, а корни уравнения (10.5) через ω₁, ω₃, ω₅, …, причём ω₀<ω₂<ω₄<…, ω₁<ω₃<ω₅<…, то для устойчивости системы необходимо и достаточно, чтобы соблюдалось следующее неравенство (условие перемежаемости корней):

ω₀< ω₁<ω₂<ω₃<ω₄<ω₅<… (10.7)

В связи с указанным следствием можно привести другую формулировку критерия устойчивости Михайлова: САУ будет устойчива тогда и только тогда, когда вещественная X(ω) и мнимая Y(ω) функции Михайлова имеют все действительные и перемежающиеся корни, причём общее число этих корней равно порядку характеристического уравнения n, и при ω=0 удовлетворяются условия

X(0)>0, Y’(0)>0.

Для уравнений до шестого порядка включительно условие перемежаемости корней даёт возможность легко провести аналитическое исследование устойчивости, не вычерчивая кривую Михайлова. При этом обычно определяют только корни уравнения Y(ω)=0. Перемежаемость корней уравнений Х(ω)=0 и Y(ω)=0 можно проверить подстановкой в Х(ω) найденных корней уравнения Y(ω)=0. Как видно из рисунка 10.8, а, знаки функции Х(ω) при подстановке возрастающих по величине корней должны чередоваться.