2-й семестр / Лекция 13

−

= ′

( , )( − ) + ′

( , )( − )

или:

′

( )( −

) + ′

( )( − ) − ( − )

= 0

Это общее уравнение плоскости. Координаты вектора нормали:

̅ = (

′

( ),

′

( ), −1),

̅

= (0; 0; 1),

̅

(̅, ̅̅̅)

1

= cos( , ̅) = ±

|̅ |∙|̅̅̅|

= ±

.

2

√1+( ′ )2+(′ )

Формула для вычисления поверхностного интеграла I типа может быть записана в виде:

( ) = ( , , ( , )) | | =

( , , ( , )) ∙ √1 + ( ′ )2 + ( ′ )2 .

Аналогично, если поверхность задана уравнением

= ( , ), Dxz – проекция на Oxz, то

( ) = ( , ( , ), ) ∙ √1 + ( ′ )2 + ( ′ )2 .

Или: если поверхность задана уравнением

= ( , ), Dyz – проекция на Oyz, то

( ) = ( ( , ), , ) ∙ √1 + ( ′ )2 + ( ′ )2 .

Пример 1. Вычислить (1 + + ) , если	- плоскость
треугольника + + = 1, > 0, > 0, > 0.

Выразим z из уравнения плоскости: = 1 − − .

Вычислим частные производные: ′ = −1, ′ = −1,

= √1 + ( ′ )2 + ( ′ )2 = √3,

(1 + + ) = √3 (1 + + 1 − − ) =

=√3 ∫01 ∫01− (2 − ) = √3 ∫01 ∫01− (2 − ) =

=√3 ∫01(2 − )(1 − ) = √3 ∫01(2 − 3 + 2) =

=√3 (2 − 32 + 13) = 5√63.

Пример 2. Вычислить ( − 3 + 2 ) , если - плоскость треугольника

4 + 3 + 2 − 4 = 0, > 0, > 0, > 0.

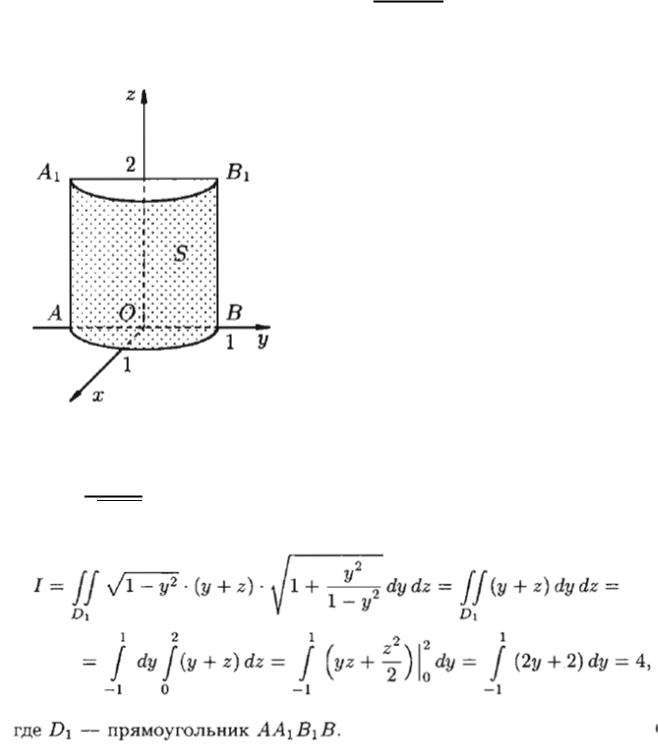
Пример 3. Вычислить ( + ) , если - часть

цилиндрической поверхности = √1 − 2, отсеченной плоскостями = 0, = 2.

Поверхность однозначно проектируется на плоскость Oyz.

′ = − √1−2, ′ = 0.

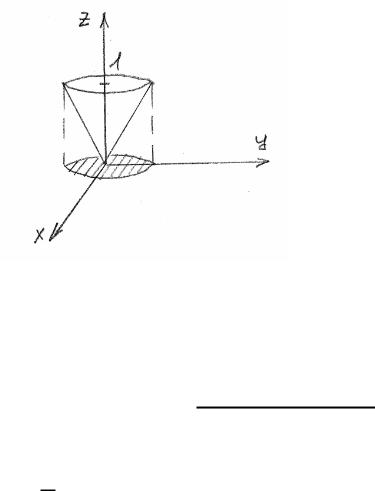
Пример 4. Вычислить ( 2 + 2) , если - часть поверхности конуса 2 = 2 + 2, заключенная между плоскостями = 0, = 1.

	= √2		+ 2, ′ =				, ′ =			.
					√ 2+ 2			√ 2+ 2

( 2 + 2) =

	=	(		2	+	2)	√1 +	2	+	2	=
								2+ 2		2+ 2

=

=√2 ( 2 + 2) = { = } =

		∫2	∫1					4 1
= √				2 = √		∙ 2 ∙					√2			.
	2				2				|	=
0			0				4		0		2

Некоторые приложения поверхностного интеграла I типа

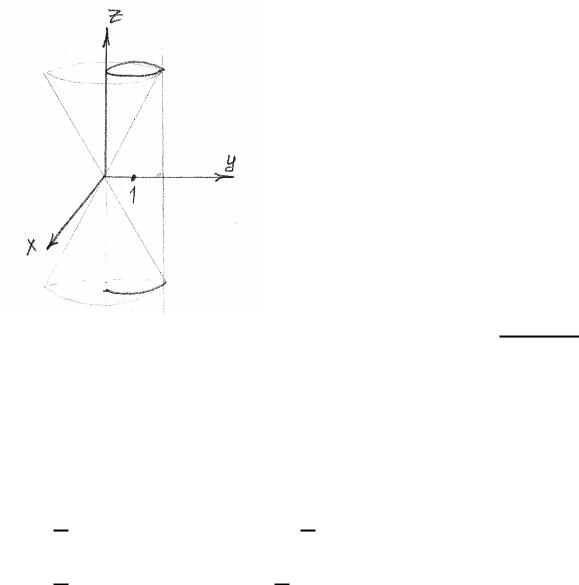
Пример 1. Найти площадь поверхности конуса

: 2 = 2 + 2,

заключенную внутри цилиндра 2 + 2 = 2 .

2 + 2 = 2 2 + ( − 1)2 = 1

Рассмотрим верхнюю часть поверхности: = √ 2 + 2

′ =

, ′

=

√2+ 2

√2+ 2

√1 +

2

2

= 2 ∫

= 2

+

=

2+ 2

2+ 2

=2√2 ∫0 ∫02 = 2√2 ∫0 2 2 =

=2√2(1 − 2 )|0 = 2√2 .

Пример 2. Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы.

Вычисление поверхностного интеграла с помощью координат на поверхности

Иногда вычисляют поверхностный интеграл путем введения координат на самой поверхности.

На цилиндрической поверхности: 2 + 2 = 2 введем

=

цилиндрические координаты: { = . Учитывая, что на

=

поверхности цилиндра = = , получаем:

=

0 ≤ ≤ 2 { = , = , {−∞ ≤ ≤ +∞.

=

Пример 1. Вычислить поверхностный интеграл

( 2 + 2) , – часть поверхности 2 + 2 = 1, вырезаемая плоскостями = 0, = 2.

=	{0 ≤ ≤ 2.
{ = , = , = ,
=	0 ≤ ≤ 2

Так как на поверхности цилиндра 2 + 2 = 1, то

( 2 + 2) = ∫02 ∫02 = 4.

Пример 2. Вычислить поверхностный интеграл

( 2 + ) , – часть поверхности 2 + 2 = 4, вырезаемая плоскостями = 0, = 3.

= 2	{0 ≤ ≤ 2
{ = 2 , = 2,
=	0 ≤ ≤ 3

( 2 + ) = ∫02 ∫03(42 + )2 =

=2 ∫02 (122 + 29) = 2 ∫02 (6 + 6 2) + 36 =

=2(6 + 3 2)|20 + 36 = 60

На сферической поверхности: 2 + 2 + 2 = 2 введем

=

сферические координаты: { = . Учитывая, что на

=

поверхности сферы = = , получаем:

= { = , = 2 , {0 ≤ ≤ 2.

=

0 ≤ ≤

Пример 1. Вычислить интеграл √2 + 2 ,

– полусфера радиуса R при ≥ 0.