Методика решения задач по оптике для студентов инженерных специальностей

***** §3.5 *****

***** §3 *****

§4. Примерырешенияиоформлениязадач

Задача 1

Определить максимальную скорость υmax фотоэлектронов, вырываемых с поверхности меди (работа выхода А = 4,39 эВ) γ – излучением с длиной волны λ = 1 пм.

1*. Дано:			Решение.
λ = 1 пм =		3*. Анализ задачи.		Максимальную
= 10−12 м,	скорость фотоэлектронов позволяет определить
	система уравнений Эйнштейна для фотоэффекта
A = 4,39 эВ ≈	(см. (4.14) – (4.16) с учетом выражения для
≈ 7,0 10−19 Дж,	энергии кванта (4.11) в §3.4):
	(1)	hν = A +Т,			где
		Т = meс2	1 -υmax2 с2	− meс2	(hν ≈ mec2 ),
	(2)
h = 6,63 10-34		Т = m υ2	2,		(hν << m	c2 ),
	(3)
		e max			e
Дж с,		W = hν = hc λ.
	(4)
с = 3 108 м/с.	Очевидно, вначале необходимо определить,
	какой следует воспользоваться формулой (2) или
	(3)? Сравним энергию падающего излучения W с
υmax – ?
	энергией покоя электрона (см. приложение 1 –
E0 = 0,51	E0 = mec2 = 0,51 МэВ = 8,16 10-14 Дж):
МэВ = 8,16	W = 6,63 10−34 3 108 1012 ≈ 1,99 10−13 Дж.
10-14 Дж.	Величины W и E0 имеют			практически один и
	тот же порядок, следовательно, необходимо
	пользоваться формулой (2).
4*. Составим	замкнутую систему уравнений.				Согласно

проведенному анализу имеем следующую систему уравнений:

- 30 -

(5)	hc λ = A + Т,
	Т = Е		1 -υ	2	с2 − Е
(6)		0				0
			max

Система	двух уравнений (5) –		(6) замкнута, так как в ней
присутствуют две неизвестные величины: Т, υmax .
5*. Решим систему уравнений			(5) – (6) относительно υmax .
Вычитая из (5) уравнение (6), имеем:
	(7) А= h c λ − Е	0	1-υ2		с2	+ Е .
			max			0
Заметим, что	в уравнении (7) A << hc λ			(см.		анализ задачи и

исходные данные), следовательно, пренебрегая величиной А, имеем:

(8)	hc	=	1		−1.
			1-υmax2
	λE0			с2

После преобразований получим

(9) υmax = c 1− hcλ+Eλ0E0 2 .

6*. Проверка размерности полученной величины υmax :

	[υ		]=	м			м Дж			м.
					1	−			=
				с
		max					Дж с м с			с
7*. Анализ решения.					Анализ формулы					(9) имеет два

аспекта:

a)максимальная скорость фотоэлектронов не зависит от работы выхода (в формуле нет величины А) электронов вещества, на поверхность которого падает γ -излучение

– вполне разумно, так как энергия γ -кванта на несколько порядков больше работы выхода электрона;

b)υmax < скорости света и абсолютное значение искомой величины зависит от соотношения величин hc и λЕ0 , причем при λ → 0 υmax → с. Это абсолютно верно, так как подкоренное выражение

λE0				1					1
				=				=			= 0 .
hc + λE					hc λE	+1			∞ +1
0			λ→0	0				λ→0

8*. Вычислим величину υmax :

- 31 -

10−12 8,16 10−13

2

8

υmax = 3 10

1

−

34

8

−12

=

−

3

10

+10

8,16 10

−13

6,63 10

=

8,16

2

(м/c).

1−

≈1,8 108

10,15

λE

2

9*. Ответ:

0

8

υmax = c

1 −

≈ 1,8 10

м/c.

hc + λE0

***************

Задача 2

На стеклянный клин с малым углом α и показателем преломления

n = 1,5 падает нормально к его грани параллельный пучок лучей

красного света с длиной волны λ = 0,7 мкм. Число возникающих

при этом интерференционных полос, приходящихся на отрезок

клина длиной L = 1 см, равно m = 11. Определить угол α клина.

1*. Дано:

2* .

λ = 0,7 мкм =

2

.C

= 7 10-7 м,

.

1

α

n = 1,5,

.

A

B

hk

hk+m

L = 1 см =

k

k+1

k+m-1

k+m

= 10-2 м,

L

m = 11.

3*.

Решение.

Анализ

задачи.

Параллельный

пучок

- 32 -

α – ? монохроматического света, падая нормально к грани клина, отражается как от верхней, так и от нижней поверхности грани (см. рис.). Эти отраженные пучки когерентны, так как берут начало от одного луча. Причем, отраженные лучи 1 и 2 света практически параллельны, так угол клина мал.

На поверхности клина будут наблюдаться в отраженном свете так называемые «полосы равной толщины» в виде темных полос, между которыми расположены светлые полосы, так как падающий свет монохроматичен! Темные полосы видны на тех участках клина, для которых разность хода лучей кратна нечетному числу полуволн света (см. формулы (2.2) и (2.3) в §3.2), при этом угол падения следует взять равным нулю (нормальное падение лучей!):

(1) = 2hk n ± λ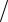2 = (2k +1)λ2 ,

где k – номер темной полосы в том месте клина, где его толщина равна hk (см. рис.).

Из приведенного рисунка, прямоугольного треугольника АВС, нетрудно получить ввиду малости угла клина, что

(2) tgα = (hk +m − hk )≈α .

L

4*. Составим полную систему уравнений для нахождения искомой величины α . К уравнению (1), описывающему разность хода для полосы с k-ым номером, необходимо добавить аналогичное уравнение для полосы с (k+m)-ым номером. Тогда с

учетом (2) имеем следующую систему уравнений:
(1)	2hk n ± λ 2 = (2k + 1)λ 2 ,
	(h	− h	)
				≈	α,
(2)	k +m	k
	L				= (2(k + m)+ 1)λ 2 .
(3)	2h	n ± λ 2
	k +m
Система трех уравнений (1)					– (3) не замкнута, так как

содержит четыре неизвестные величины: hk , hk +m , k, α . Однако уравнения (1) – (3) линейно зависимы относительно переменных

- 33 -

hk , hk +m , k , то есть полученную систему нам не удастся

разрешить относительно любой из этих переменных. Между тем решить систему (1) – (3) нам необходимо относительно α , и это сделать можно.

5*. Решим систему уравнений (1) – (3) относительно α .

Обозначив hk +m − hk = Σ и вычитая из (3) уравнение (1), получим:

		(4)	Σn = m λ 2,
			Σ
				≈ α.
		(5)	L
Разделив почленно (4) на (5), находим:
		(6)	α =		mλ	.
					2nL
6*. Проверка размерности полученной величины α :
[α	]= м	=1, единица измерения – рад (см. приложение 2).
7*.	м
	Анализ решения. Показатель преломления n в формуле

(6) находится в знаменателе, следовательно, угол клина растет при уменьшении величины n (nmin=1 – воздух) – вполне разумно, так как наилучшие результаты по наблюдению интерференционных картин мы имеем на установке «кольца Ньютона», где в качестве клина используется воздушная прослойка.

8*. Вычислим величинуα :

α =	11 7 10-7		≈ 2,6 10-4 (рад)≈ 2,6 10-4 (рад) 2,1 105		''
	2	1,5 10-2
					рад

≈5,5 10′′.

9*. Ответ: α = 2mnLλ ≈ 2,6 10−4 рад ≈ 5,5 10′′ .

***************

Задача 3

Два николя N1 и N2 расположены так, что угол между их

оптическими осями равен ϕ = 60o. Определить, во сколько раз θ

уменьшится интенсивность естественного света при прохождении через оба николя, если коэффициент поглощения в николе N1

- 34 -

k1 = 0,05, в николе

N2

–

k2 = 0,07.

Потерями на отражение

пренебречь.

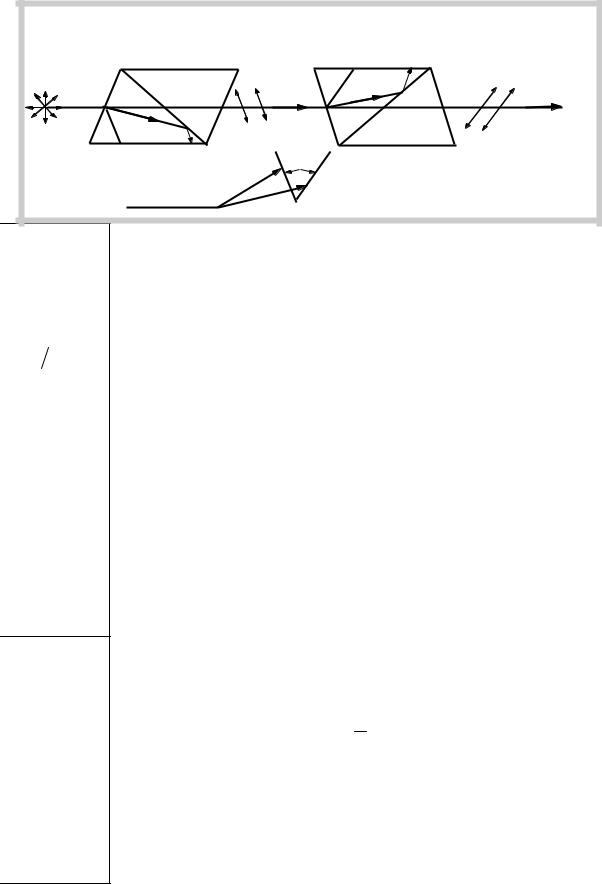
2* .

I1e=1/2I0

(1-k1 )

A1

I2e=1/2I0 (1-k1 )(1-k2 )cos 2ϕ

I0 B

o

e

e

B1

o

A

B

ϕ

B1

оптические

оси

A A1

1*.

Решение.

Дано:

3*. Анализ задачи.

Естественный свет, падая

на николь, дает начало двум электромагнитным

ϕ = 60o =

волнам: необыкновенной (е) и обыкновенной (о)

= π 3рад,

(для простоты рассуждений рассматриваем только

две волны). Обе волны (допускается использовать

термин «лучи») одинаковы по интенсивности (см.

k = 0,05,

формулы (2.26) и (2.27) в §3.2) и полностью

1

поляризованы

во

взаимно

перпендикулярных

k2 = 0,07.

плоскостях.

Плоскость

колебаний

необыкновенного луча лежит в плоскости главного

сечения (см. рис.). Обыкновенный же луч нас вовсе

не интересует, так как поглощается специальной

призмой, закрепленной на боковой грани николя

(см. рис. ниже).

Итак, если обозначить интенсивность

θ – ?

естественного света через I0 , то интенсивность

необыкновенного луча на выходе из первого

кристалла с учетом поглощения равна

(1) I

1e

=

1

I

0

(1− k ).

2

1

Линейно поляризованный свет интенсивности

I1e , падая на второй николь, также расщепляется на

два луча различной интенсивности: обыкновенный

(он нас по той же причине не интересует) и

необыкновенный,

интенсивность

которого

- 35 -

определяется законом Малюса (см. (2.23) в §3.2). Учитывая потери интенсивности на поглощение во втором николе, имеем на выходе из N2 :

(2) I2e = I1e (1− k2 )cos2 ϕ , где

ϕ − угол между оптическими осями николей,

являющимися плоскостями пропускания поляризованного света.

Искомое уменьшение интенсивности найдем делением интенсивности исходной I0 на

интенсивность на выходе из второго николя I2e :

(3) θ = I0 I2e .

4*. Составим полную систему уравнений для нахождения искомой величины θ :

(1) I1e = 12 I0 (1 − k1 ),

(2) I2e = I1e (1 − k2 )cos2 ϕ,(3) θ = I0 I2e .

Система трех уравнений (1) – (3) не замкнута, так как содержит четыре неизвестные величины: I0 , I1e , I2e , θ . Однако

уравнения (1) – (3) линейно зависимы относительно переменных I0 , I1e , I2e , то есть полученную систему нам не удастся

разрешить относительно любой из этих переменных. Между тем решить систему (1) – (3) нам необходимо относительно θ , и это нетрудно сделать.

5*. Решим систему уравнений		(1)		– (3)	относительно θ .
Подставляя (1) и (2), с учетом (3) получим:
(4) θ =		2				.
	(1− k )(1− k		2	)cos2	ϕ
1

6*. Проверка размерности полученной величины θ :

[θ]= 11 =1, единица измерения отсутствует.

7*. Анализ решения. Полученную формулу (4) интересно проанализировать в двух случаях:

- 36 -

a) k1 и k2 стремятся к нулю (нет потерь), следовательно,

искомая величина θ растет – вполне разумно (никаких уменьшений интенсивности нет); k1 и k2 стремятся к

единице (потери огромные), следовательно, искомая

величина θ стремится к	бесконечности – вполне
разумно (на выходе из кристалла света нет).
b) угол ϕ → 0, cosϕ =1,	искомая величина θ

максимальна для данных николей – вполне разумно, так как плоскости пропускания кристаллов параллельны; ϕ =π / 2, cosϕ = 0, искомая величина θ стремится к

бесконечности – логично, так как плоскости пропускания николей скрещены, и на выходе из второго кристалла «ничего нет».

8*. Вычислим величину θ :

θ =			2		=		2	≈ 9,1.
	(1− 0,05)(1−0,07)cos2 (π 3)					0,95 0,93* 0,25
9*. Ответ:		θ =	2				≈ 9,1.
				(1 − k1 )(1 − k2 )cos2 ϕ

***************

Задача 4

Линейно поляризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластину толщиной L, интенсивность пучка света после поляроида стала равна θ = 14 интенсивности пучка,

падающего на поляроид. Определить	минимальную	толщину
Lmin , если постоянная вращения	кварцевой	пластины
α0 = 50 град/мм; поглощением и	отражением	света в

поляроиде и пластинке можно пренебречь.

- 37 -

1*. Дано:

α0		= 50	град		=
			мм
=		50π рад				,
180 *10-3 м
θ = 1 4.

Lmin – ?

Решение.

3*. Анализ задачи. Полное гашение света поляроидом означает, что оптическая ось поляроида и плоскость поляризации падающего света скрещены (взаимно перпендикулярны) (см. рис., а)). Введение кварцевой пластины приводит к повороту плоскости поляризации света (см. рис., б)) на угол ϕ (неважно, по или против часовой

стрелке) согласно закону для оптически активных кристаллов (см. формулу 2.24 в §3.2):

(1)ϕ = α0 Lmin ,

где Lmin −геометрическая длина пути света в

кристалле.

Закон Малюса (см. формулу 2.23 в §3.2) позволяет найти интенсивность I1

поляризованного света, прошедшего через кварцевую пластину и поляроид:

(2)I1 = I0 cos2 β,

где I0 – интенсивность света на входе в

пластину, β − угол между плоскостью поляризации

света и оптической осью поляроида (см. рис.,

б).

Связь углов β и ϕ нетрудно установить

из рисунка:

(3) β = π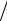2 −ϕ .

- 38 -

2*.	а)		б)	θ	I0
	плоскость поляризации			I1 =
	падающего света
		I1 =0
		v	пластина	v
		E		E
				β
	I 0		E
		поляроид		ϕ
оптическая ось
поляроида
		I0		L

4*. Составим полную систему уравнений для нахождения искомой величины Lmin , если учтем, что отношение интенсивностей I1 и I0 равно θ :

(1)	ϕ = α0 Lmin ,
	I1 = I0 cos2 β ,
(2)
	β = π 2 −ϕ,
(3)
	θ = I1 I0 .
(4)

Система четырех уравнений (1) – (4) не замкнута, так как содержит пять неизвестных величин: I0 , I1, ϕ, β, Lmin . Однако

следует заметить, что уравнения (2) и (4) линейно зависимы относительно переменных I0 , I1 . Между тем решить систему (1) –

(4) относительно Lmin не представляет большого труда.

5*. Решим систему уравнений (1) – (4) относительно Lmin .

Подставляя (2) в (4), после простых преобразований получим систему трех уравнений с тремя неизвестными:

(1) ϕ = α0 Lmin ,(3) β = π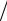2 −ϕ,

(5) θ = cos2 β .

После подстановки уравнения (1) в (3), а затем в (5) имеем:

(6) cos2 (π 2 −α	0	L	)=θ или
		min
- 39 -