7.11. Метод кубической аппроксимации

По своей эффективности метод кубической аппроксимации является одним из самых лучших среди всех методов одномерной оптимизации. Недостатком является необходимость вычисления первой производной.

Предположим, что функция f (x) выпукла и непрерывно дифференцируема на отрезке [a,b], f '(a)<0, f '(b)>0. Аппроксимируем функцию многочлена 3-й степени:

ϕ(x) = c0 (x − a)3 + c1(x − a)2 + c2 (x − a) + c3,

где коэффициенты c0, c1, c2, c3 определяются из условий:

ϕ(a) = f (a) => c3 = f (a),
ϕ'(a) = f '(a)	=> c2 = f '(a),
ϕ(b) = f (b) => c (b − a)3 + c (b − a)2		+ c (b − a) + c = f (b),
0	1	2	3
ϕ'(b) = f '(b) => 3c (b − a)2 + 2c (b − a) + c = f '(b).
0	1		2

Найдем точку

x = argminϕ(x)

[a,b]

Легко проверить, что

				= a +γ (b − a), где
			x
	γ =					z +ω − f '(a)		;
						f '(b) − f '(a) + 2ω
z = 3		f (a) − f (b)					+ f '(a) + f '(b),
					b − a

ω = z 2 − f '(a) f '(b)

Точка x используется для сжатия отрезка локализации так же, как и в методе деления отрезка пополам с вычислением производной: если

f '(		) < 0,	то новым отрезком локализации является отрезок [				,b], если
	x					x
f '(		) > 0,	то отрезок[a,		].
	x			x
			81

Алгоритм метода кубической аппроксимации:

1.Задается начальное приближение x0 , шаг h, погрешность ε.

2.Вычисляется f '(x0 ).

3.Проверка условия f '(x0 ) < 0 :

–если "да", то x1 = x0 + 2k h ;

–иначе, x1 = x0 − 2k h .

4.Проверяется условие: f '(x1 ) f '(x0 ) < 0 :

–если "да", то точка min-ма функции пройдена и следует переходить к пункту 5;

–иначе, x0=x1 и возврат на п.2.

5.

Если

f '(x0 ) < 0,

a = x0

a = x1

то b = x

, иначе b = x .

1

0

6.

Расчет точки min-ма кубического полинома

.

x

7.

Если

f '(

) < 0,

то a =

, т.к.

x* [

,b] , если нет, то b =

, т.к.

x

x

x

x

x* [a,

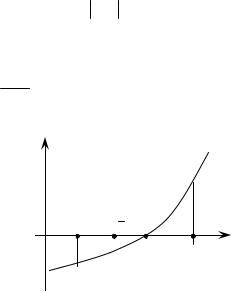
] (см. рис.13).

x

8.Проверка условия b −a < ε :

–если "да", то переход на п.9;

–иначе, переход на п.6.

9. x* = b +2 a , min f = f (x* ), f 1 = f '(x* ).

Печать x*, min f, f1. Конец. f '(x)

f '(b)

a x

x* b

f '(a)

Рис.13.

82

7.12. Метод Фибоначчи

Этот метод связан со знаменитыми числами Фибоначчи, которые представляют собой последовательность, где каждый элемент получается, как сумма двух предыдущих. Числа Фибоначчи определяются соотношениями

Pn+2 = Pn+1 + Pn , n =1,2,3,...; P1 = P2 =1

Метод Фибоначчи относится к классу симметричных методов нулевого порядка и применяется для унимодальных функций. Причем абсолютная погрешность, возникающая при поиске минимума этим методом, не превышает величины

eps = (b −a) / Ps ,

где Ps – s-тое число в ряде Фибоначчи.

Алгоритмы метода "золотого" сечения и метода Фибоначчи очень похожи, отличия заключаются в том, что в методе "золотого" сечения отрезок всегда делится в постоянном соотношении, в то время как в методе Фибоначчи деление отрезка на каждой итерации осуществляется в зависимости от чисел Фибоначчи. Кроме того, метод Фибоначчи в среднем на 17% быстрее метода золотого сечения. Между числами Фибоначчи и методом золотого сечения существует связь:

lim	Pn	=	−1	+ 5
				2
n→∞ P
	n+1

Алгоритм метода Фибоначчи:

1.Задаем интервал поиска [a,b] и погрешность ε.

2.P[1] = 1; P[2] = 1; n = 2.

3.Вычисляем очередное число Фибоначчи:

P[n+1] = P[n] + P[n-1]

4.Находим координаты точки x1 [a,b], которая делит отрезок в отношении двух чисел Фибоначчи:

83

			x = b −		P[n]	(b − a)
			1		P[n +1]
(Первое	x = b − 2	3	(b − a)	, второе		x = b − 3	5	(b − a)	и т.д.)
	1					1

5.Определяем координаты точки x2, которая является зеркальным отражением точки x1 относительно центра отрезка:

	x2 = a +	P[n]	(b − a)
		P[n +1]

6.Если условие f(x1) > f(x2) выполняется, то a = x1, иначе b = x2.

7.n = n + 1

8.Если условие окончания поиска |b − a| ≤ ε не выполняется, то переходим к следующему числу Фибоначчи (на п.3).

9.В качестве минимального значения принимаем ту из точек a или b, в которой целевая функция имеет наименьшее значение.

7.13.Метод Ньютона 2-го порядка

Метод Ньютона используется для гладких f0(x) функций. Минимизируемая функция f0(x) в малой окрестности произвольной точки х0, расположенной вблизи точки минимума х*, может быть аппроксимирована усеченным рядом Тейлора:

f0 (x) ≈ f0 (x0 ) + f0 '(x0 ) (x − x0 ) + 0,5	(7.19)
f0"(x0 ) (x − x0 )2 +... .

Продифференцируем (7.19) по х, учитывая, что f0(x0) и f0'(x0) являются постоянными величинами. Применяя необходимое условие оптимальности получим:

f0 '(x) = 0 ≈ f0 '(x0 ) + f0"(x0 ) (x − x0 ) .

Следовательно, выражение для вычисления приближенного значения точки экстремума будет иметь вид:

84

1

0

f

0

'(x0 )

x

= x

−

f0"(x0 )

,

Если

f

0

'(x0 )

> ε

, то ищем x2

= x1 −

f

0

'(x1)

и т.д.

f0"(x

0

)

1

f0"(x )

Для произвольной k-ой итерации имеем

x

k +1

= x

k

−

f0 '(xk )

, при k=0,1,2,...,

(7.20)

f0"(xk )

Итерационный процесс прекращается, когда

f0 '(xk )

≤ ε ,

(7.21)

f0"(x

k

)

т.е. xk +1 = xk −

x , где

x = f0 '(xk ) f0"(xk ).

Метод является прямым обобщением известного метода Ньютона отыскания корня функции ϕ(x) = 0.

Уравнение касательной к кривой в точке х0:

y= y(x0 ) − y '(x0 ) (x0 − x).

Вточке х пересечение касательной с осью абсцисс:

y = y(x) = 0 => x = x0 − y(x0 ) . y '(x0 )

Необходимое условие экстремума функции f0(х):

f0'(x)=0

Тогда обозначим, ϕ(x) = f0 '(x) получим то же уравнение (7.20). Начальное приближение выбирается из условия

ϕ(x0 ) ϕ"(x0 ) > 0

или

f0 '(x0 ) f0 '''(x0 ) > 0.	(7.22)
	85