Лабораторные работы / Лабораторная работа 3 / Решение системы линейных уравнений методом Гаусса (Машеров)

Национальный исследовательский институт

Московский Энергетический Институт (Технический Университет)

Институт автоматики и вычислительной техники

Кафедра Прикладной математики

Лабораторная работа №3

по дисциплине «Параллельные системы и параллельное программирование»

тема: «Решение системы линейных уравнений методом Гаусса с использованием нитевого распараллеливания.»

Выполнил:

Машеров Д.Е.

А-13-08

Москва

2012 г.

Постановка задачи

Дана линейная система уравнений,представленная в матричном виде, требуется найти решение этой системы с помощью метода Гаусса, используя принципы нитевого (threads) распараллеливания.

Последовательный алгоритм.

Метод Гаусса – широко известный прямой алгоритм решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными. Если система линейных уравнений невырожденна, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы (8.2)) к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.

Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду

,

где матрица коэффициентов получаемой системы имеет вид

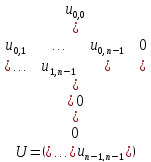
На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной , после этого из предпоследнего уравнения становится возможным определение переменной и т.д.

Прямой ход алгоритма Гаусса

Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0i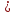n-1, метода производится исключение неизвестной i для всех уравнений с номерами k, большими i (т.е. i<kn-1 ). Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу (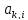/ 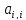), с тем чтобы результирующий коэффициент при неизвестной 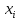в строках оказался нулевым.

Обратный ход алгоритма Гаусса

После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной 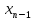, после этого из предпоследнего уравнения становится возможным определение переменной и т.д.

Параллельный алгоритм.

В основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b.

Выделение информационных зависимостей

Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами.

Для выполнения прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду.

Выполнение итерации i, 0<=i<n-1, прямого хода метода Гаусса включает ряд последовательных действий. Получив строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной .

При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Далее подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.

Результаты вычислительного эксперимента

Эксперементы осуществлялись на компьютере с процессором Intel i7 Сore 950(4 ядра)

1. Размерность матрицы 5 000 * 5 000

Число исполнителей	Время решения, секунд	Ускорение
1	272,667
2	144,183	1,89
3	102,892	2,65
4	94,723	2,88
5	93,211	2,93
6	82,778	3,29
7	74,29	3,67
8	69,009	3,95

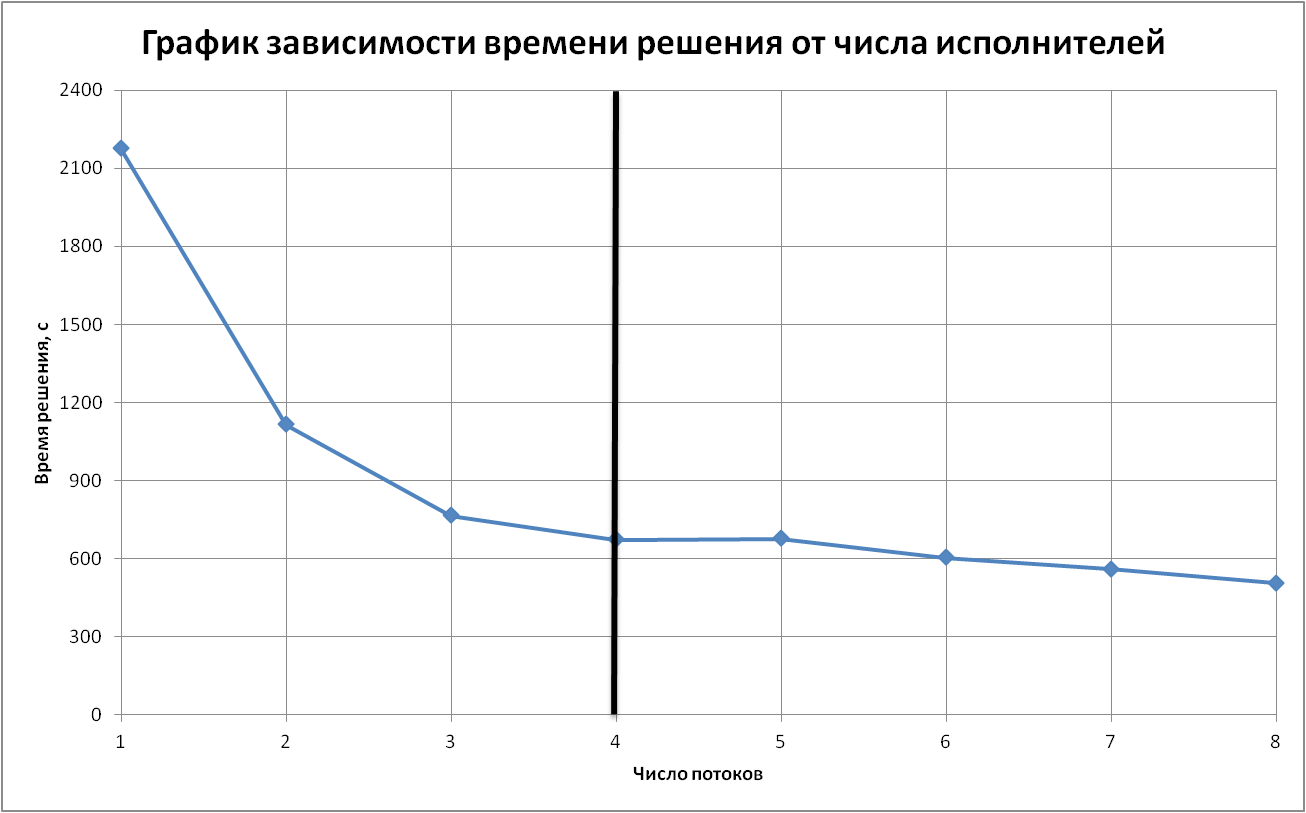
2. Размерность матрицы 10 000 * 10 000

Число исполнителей	Время решения, секунд	Ускорение
1	2174,58
2	1115,066	1,95
3	765,773	2,84
4	673,226	3,23
5	676,32	3,22
6	603,849	3,60
7	559,695	3,89
8	504,776	4,31