Лабораторные работы / Лабораторная работа 2 / Поиск минимального оставного дерева (Машеров)
.docxНациональный исследовательский институт
Московский Энергетический Институт (Технический Университет)
Институт автоматики и вычислительной техники
Кафедра Прикладной математики
Лабораторная работа №2
по дисциплине «Параллельные системы и параллельное программирование»
тема: «Поиск минимального оставного дерева.»
Выполнил:
Машеров Д.Е.
Проверил:
Панков Н.А.
Москва
2012 г.
Постановка задачи
Дана граф, требуется найти минимальное оставное дерева этого графа.
Охватывающим деревом (или остовом ) неориентированного графа G называется подграф T графа G, который является деревом и содержит все вершины из G. Определив вес подграфа для взвешенного графа как сумму весов входящих в подграф дуг, под минимально охватывающим деревом (МОД) T понимается охватывающее дерево минимального веса.
Последовательный алгоритм.
Используется алгоритм Прима.
Алгоритм
начинает работу с произвольной вершины
графа, выбираемой в качестве корня
дерева, и в ходе последовательно
выполняемых итераций расширяет
конструируемое дерево до МОД. Пусть
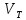есть множество вершин, уже включенных
алгоритмом в МОД, а величины
,
1<=
<=n, характеризуют дуги минимальной
длины от вершин, еще не включенных в
дерево, до множества
,
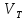т.е.
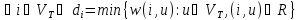
(если для
какой-либо вершины не существует ни
одной дуги в
,
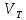значение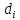
устанавливается равным ). В начале
работы алгоритма выбирается корневая
вершина МОД s и полагается
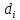={s},
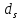=0.
Действия, выполняемые на каждой итерации алгоритма Прима, состоят в следующем:
-
определяются значения величин di для всех вершин, еще не включенных в состав МОД;
-
выбирается вершина t графа G, имеющая дугу минимального веса до множества ;
-
вершина t включается в VT.
После выполнения n-1 итерации метода МОД будет сформировано. Вес этого дерева может быть получен при помощи выражения
Параллельный алгоритм.
Итерации метода должны выполняться последовательно и, тем самым, не могут быть распараллелены. С другой стороны, выполняемые на каждой итерации алгоритма действия являются независимыми и могут реализовываться одновременно.
Распределение данных между процессорами вычислительной системы должно обеспечивать независимость перечисленных операций алгоритма Прима. Это может быть реализовано, если каждая вершина графа располагается на процессоре вместе со всей связанной с вершиной информацией.
-
набор вершин
-
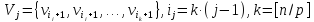
соответствующий этому набору блок из k величин
-
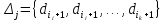
вертикальную полосу матрицы смежности графа G из k соседних столбцов
,
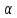есть
s-ый стольбец матрицы А
-
общую часть набора Vj и формируемого в процессе вычислений множества вершин
.
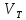Результаты вычислительного эксперимента
-
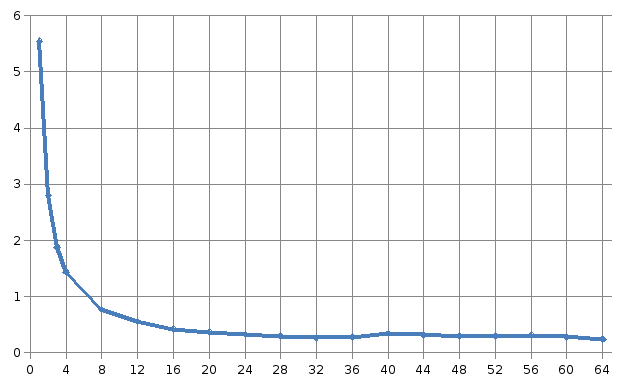
Количество вершин графа: 1 000
|
Число исполнителей |
Время решения |
Ускорение |
|
1 |
5,547534 |
|
|
2 |
2,791276 |
1,91 |
|
3 |
1,88332 |
2,98 |
|
4 |
1,433112 |
4,02 |
|
8 |
0,774494 |
8,03 |
|
12 |
0,556577 |
11,28 |
|
16 |
0,418985 |
13,79 |
|
20 |
0,367053 |
15,22 |
|
24 |
0,326834 |
16,40 |
|
28 |
0,299249 |
17,41 |
|
32 |
0,266754 |
18,56 |
|
36 |
0,277727 |
11,41 |
|
40 |
0,346345 |
14,27 |
|
44 |
0,323366 |
12,07 |
|
48 |
0,296411 |
13,43 |
|
52 |
0,295205 |
11,27 |
|
56 |
0,31282 |
8,62 |
|
60 |
0,285301 |
7,52 |
|
64 |
0,242074 |
17,69 |
-
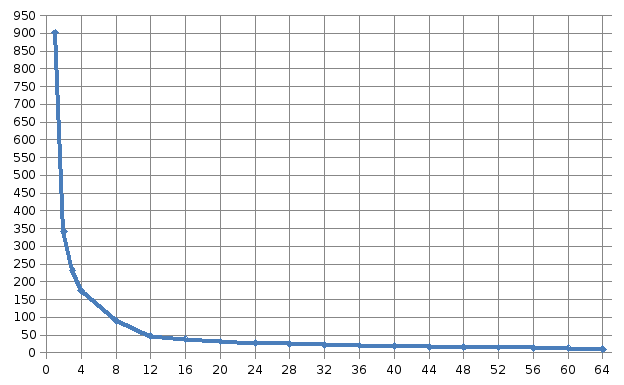
Количество вершин графа: 5 000
|
Число исполнителей |
Время решения |
Ускорение |
|
1 |
902,03109 |
|
|
2 |
342,68127 |
2,63 |
|
3 |
232,899105 |
3,93 |
|
4 |
175,10955 |
5,14 |
|
8 |
90,308224 |
10,24 |
|
12 |
47,578303 |
15,07 |
|
16 |
39,038579 |
19,43 |
|
20 |
32,30373 |
23,46 |
|
24 |
27,843325 |
27,85 |
|
28 |
25,298673 |
31,91 |
|
32 |
22,473695 |
36,01 |
|
36 |
20,695048 |
39,49 |
|
40 |
18,728376 |
43,14 |
|
44 |
17,164971 |
46,54 |
|
48 |
16,130638 |
49,27 |
|
52 |
15,016155 |
51,99 |
|
56 |
13,954162 |
55,59 |
|
60 |
13,285935 |
57,88 |
|
64 |
10,253616 |
61,45 |
-
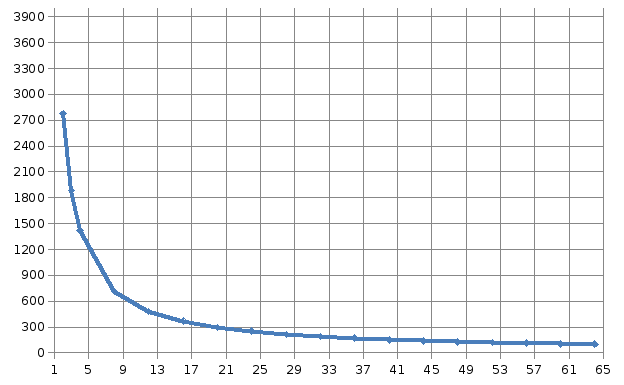
Количество вершин графа: 10 000
|
Число исполнителей |
Время решения |
|
2 |
2774,1043 |
|
3 |
1882,915374 |
|
4 |
1416,6679 |
|
8 |
713,6579 |
|
12 |
482,27567 |
|
16 |
368,15783 |
|
20 |
294,24421 |
|
24 |
250,46335 |
|
28 |
214,14437 |
|
32 |
188,42947 |
|
36 |
171,45674 |
|
40 |
152,31577 |
|
44 |
140,24903 |
|
48 |
129,80971 |
|
52 |
120,93132 |
|
56 |
112,64522 |
|
60 |
105,99757 |
|
64 |
100,04801 |
-
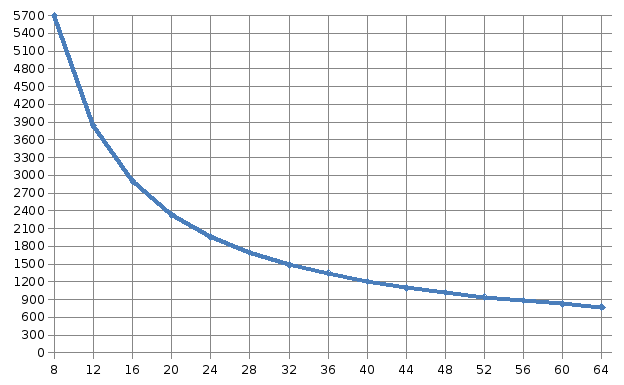
Количество вершин графа: 20 000
|
Число исполнителей |
Время решения |
|
8 |
5698,3759 |
|
12 |
3838,5841 |
|
16 |
2909,7297 |
|
20 |
2333,4545 |
|
24 |
1962,7721 |
|
28 |
1698,1574 |
|
32 |
1486,6888 |
|
36 |
1347,5227 |
|
40 |
1206,1265 |
|
44 |
1101,3858 |
|
48 |
1021,4873 |
|
52 |
942,69882 |
|
56 |
888,52427 |
|
60 |
829,63986 |
|
64 |
771,18603 |
-
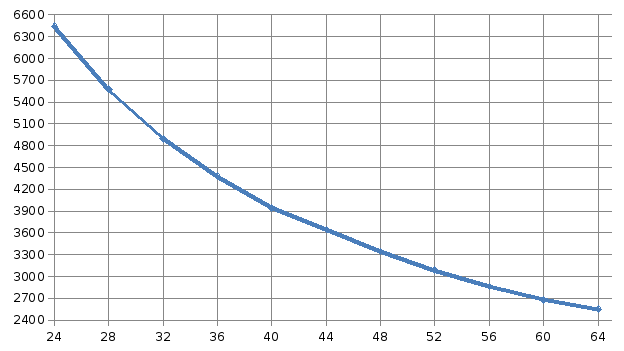
Количество вершин графа: 30 000
|
Число исполнителей |
Время решения |
|
24 |
6444,4012 |
|
28 |
5578,5286 |
|
32 |
4897,1726 |
|
36 |
4381,5045 |
|
40 |
3946,59 |
|
44 |
3647,9182 |
|
48 |
3344,2485 |
|
52 |
3089,6803 |
|
56 |
2862,2789 |
|
60 |
2680,8999 |
|
64 |
2549,2176 |
