Лабораторные работы / Лабораторная работа 1 / Решение системы линейных уравнений методом Гаусса (Машеров)
.docxНациональный исследовательский институт
Московский Энергетический Институт (Технический Университет)
Институт автоматики и вычислительной техники
Кафедра Прикладной математики
Лабораторная работа №1
по дисциплине «Параллельные системы и параллельное программирование»
тема: «Решение системы линейных уравнений методом Гаусса.»
Выполнил:
Машеров Д.Е.
Проверил:
Панков Н.А.
Москва
2012 г.
Постановка задачи
Дана линейная система уравнений,представленная в матричном виде, требуется найти решение этой системы с помощью метода Гаусса.
Последовательный алгоритм.
Метод Гаусса – широко известный прямой алгоритм решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными. Если система линейных уравнений невырожденна, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы (8.2)) к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.
Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду
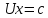 ,
,
где матрица коэффициентов получаемой системы имеет вид
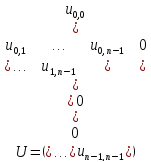
На обратном
ходе метода Гаусса (второй этап алгоритма)
осуществляется определение значений
неизвестных. Из последнего уравнения
преобразованной системы может быть
вычислено значение переменной
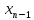 ,
после этого из предпоследнего уравнения
становится возможным определение
переменной
,
после этого из предпоследнего уравнения
становится возможным определение
переменной
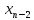 и
т.д.
и
т.д.
Прямой ход алгоритма Гаусса
Прямой
ход метода Гаусса состоит в последовательном
исключении неизвестных в уравнениях
решаемой системы линейных уравнений.
На итерации i, 0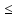 i
i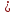 n-1,
метода производится исключение
неизвестной i для всех уравнений с
номерами k, большими i (т.е. i<k
n-1,
метода производится исключение
неизвестной i для всех уравнений с
номерами k, большими i (т.е. i<k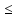 n-1
). Для этого из этих уравнений осуществляется
вычитание строки i, умноженной на
константу (
n-1
). Для этого из этих уравнений осуществляется
вычитание строки i, умноженной на
константу (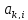 /
/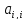 ), с тем чтобы результирующий коэффициент
при неизвестной
), с тем чтобы результирующий коэффициент
при неизвестной
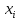 в строках оказался нулевым.
в строках оказался нулевым.
Обратный ход алгоритма Гаусса
После
приведения матрицы коэффициентов к
верхнему треугольному виду становится
возможным определение значений
неизвестных. Из последнего уравнения
преобразованной системы может быть
вычислено значение переменной
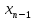 ,
после этого из предпоследнего уравнения
становится возможным определение
переменной
,
после этого из предпоследнего уравнения
становится возможным определение
переменной
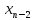 и т.д.
и т.д.
Параллельный алгоритм.
В основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b.
Выделение информационных зависимостей
Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами.
Для выполнения прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду.
Выполнение итерации i, 0<=i<n-1, прямого хода метода Гаусса включает ряд последовательных действий.
Подзадача
на текущей итерации должна разослать
свою строку матрицы A и соответствующий
элемент вектора b всем остальным
подзадачам с номерами k, k<i. Получив
строку, подзадачи выполняют вычитание
строк, обеспечивая тем самым исключение
соответствующей неизвестной
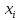 .
.
При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i, 0<=i<n-1, определяет значение своей переменной xi, это значение должно быть разослано всем подзадачам с номерами k, k<i. Далее подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.
Результаты вычислительного эксперимента
-
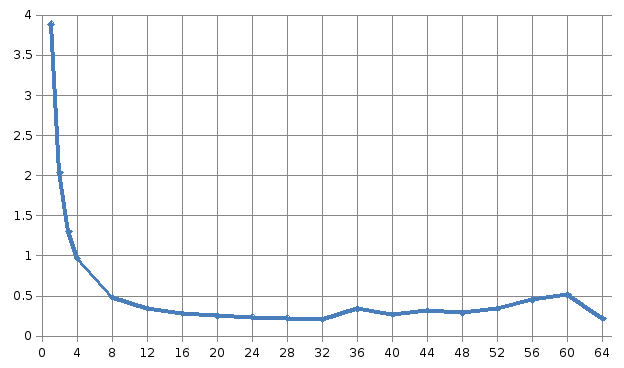
Размерность матрицы 1 000 * 1 000
|
Число исполнителей |
Время решения |
Ускорение |
|
1 |
3,889885 |
|
|
2 |
2,03947 |
1,91 |
|
3 |
1,303311 |
2,98 |
|
4 |
0,968705 |
4,02 |
|
8 |
0,484176 |
8,03 |
|
12 |
0,344847 |
11,28 |
|
16 |
0,282161 |
13,79 |
|
20 |
0,255538 |
15,22 |
|
24 |
0,237215 |
16,40 |
|
28 |
0,223481 |
17,41 |
|
32 |
0,20956 |
18,56 |
|
36 |
0,340974 |
11,41 |
|
40 |
0,272545 |
14,27 |
|
44 |
0,322168 |
12,07 |
|
48 |
0,289613 |
13,43 |
|
52 |
0,345245 |
11,27 |
|
56 |
0,451369 |
8,62 |
|
60 |
0,516958 |
7,52 |
|
64 |
0,219884 |
17,69 |
-
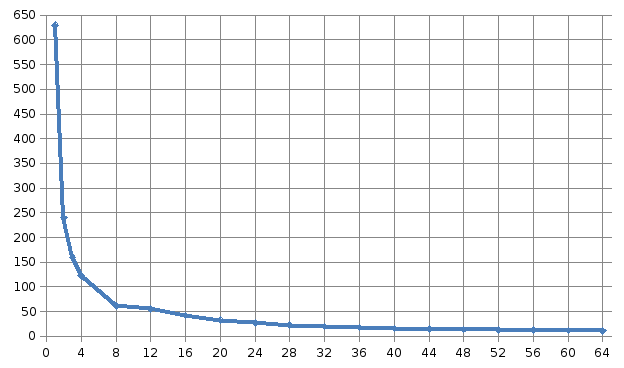
Размерность матрицы 5 000 * 5 000
|
Число исполнителей |
Время решения |
Ускорение |
|
1 |
630,05706 |
|
|
2 |
239,864168 |
2,63 |
|
3 |
160,254289 |
3,93 |
|
4 |
122,548024 |
5,14 |
|
8 |
61,526579 |
10,24 |
|
9 |
55,125141 |
11,43 |
|
12 |
41,80622 |
15,07 |
|
16 |
32,426099 |
19,43 |
|
20 |
26,851851 |
23,46 |
|
24 |
22,620907 |
27,85 |
|
28 |
19,744682 |
31,91 |
|
32 |
17,498558 |
36,01 |
|
36 |
15,955906 |
39,49 |
|
40 |
14,606562 |
43,14 |
|
44 |
13,538249 |
46,54 |
|
48 |
12,78833 |
49,27 |
|
52 |
12,119593 |
51,99 |
|
56 |
11,333663 |
55,59 |
|
60 |
10,886192 |
57,88 |
|
64 |
10,253616 |
61,45 |
-
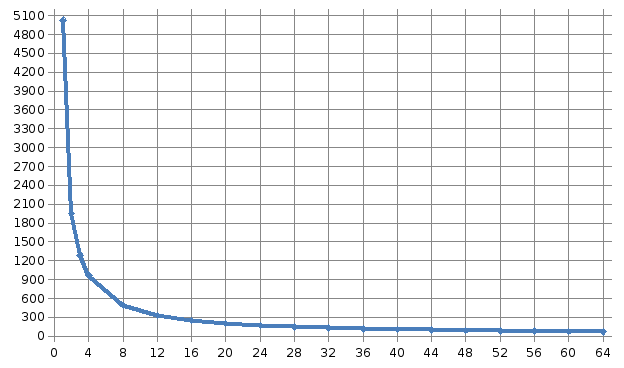
Размерность матрицы 10 000 * 10 000
|
Число исполнителей |
Время решения |
Ускорение |
|
1 |
5028,199327 |
|
|
2 |
1945,037546 |
2,59 |
|
3 |
1291,534027 |
3,89 |
|
4 |
970,241249 |
5,18 |
|
8 |
488,238341 |
10,30 |
|
12 |
330,517302 |
15,21 |
|
16 |
251,358222 |
20,00 |
|
20 |
202,685559 |
24,81 |
|
24 |
171,665325 |
29,29 |
|
28 |
148,61511 |
33,83 |
|
32 |
132,072106 |
38,07 |
|
36 |
117,686683 |
42,73 |
|
40 |
107,498263 |
46,77 |
|
44 |
98,736844 |
50,93 |
|
48 |
90,612731 |
55,49 |
|
52 |
84,959972 |
59,18 |
|
56 |
79,143356 |
63,53 |
|
60 |
74,60013 |
67,40 |
|
64 |
70,671518 |
71,15 |
-
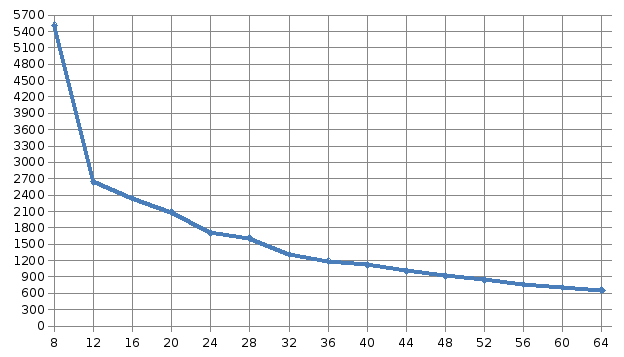
Размерность матрицы 20 000 * 20 000
|
Число исполнителей |
Время решения |
|
8 |
5513,812622 |
|
12 |
2643,405368 |
|
16 |
2335,40993 |
|
20 |
2085,484199 |
|
24 |
1708,068046 |
|
28 |
1608,645288 |
|
32 |
1313,068484 |
|
36 |
1186,850485 |
|
40 |
1124,312945 |
|
44 |
1010,315608 |
|
48 |
918,527887 |
|
52 |
849,721883 |
|
56 |
760,312795 |
|
60 |
704,409915 |
|
64 |
660,028108 |
-
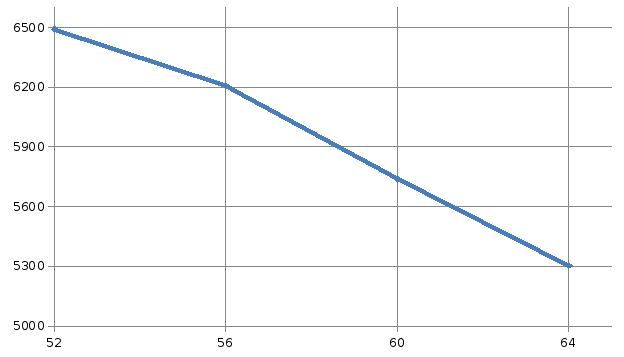
Размерность матрицы 40 000 * 40 000
|
Число исполнителей |
Время решения |
|
52 |
6491,153326 |
|
56 |
6208,691701 |
|
60 |
5739,720201 |
|
64 |
5304,103673 |