Векторы

Вектор – сонаправленный отрезок. Обозначается или .

Вектор называется нулевым, если начало и конец вектора совпадают.

Длина или модуль вектора обозначается .

Два вектора называются равными, если:

1. Они лежат на одной прямой или на параллельных прямых

2. Имеют одинаковое направление

3. Имеют одинаковую длину.

Два вектора называются коллинеарными, если они лежат на одной или параллельных прямых.

Три вектора называются компланарными, если они лежат в одной плоскости.

Операции над векторами

1. Сложение векторов

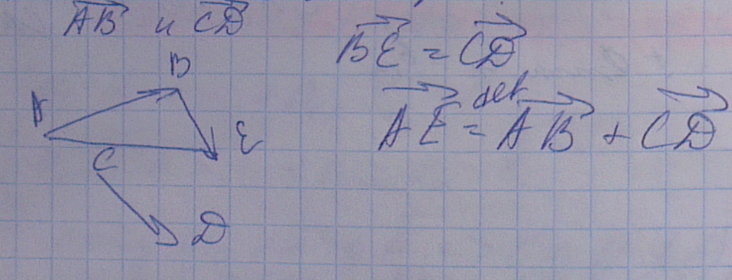
2. Умножение вектора на число

1. 

2. 

Т. Пусть коллинеарные векторы, значит существует число, такое, что .

Доказательство.

Единственность. (от противного) , выводим, получаем б1=б2. Такие дела.

Свойства сложения векторов и умножения на число (аксиомы векторного пространства)

1. A+b=b+a.

2. A+b+c – диагональ куба.

3. Существует такой ноль вектор, что для любого а: а+0=а

4. Для любого а существует –а, такое что а+(-а)=0

5. – дистрибутивность

6. – дистрибутивность

7. 

8. 1*а=а

Векторное пространство

Действительным или вещественным векторным пространством назовем множество элементов, которое будем называть векторами, на котором заданы две операции сложения и умножения вектора на действ. Число, при выполнении свойств 1-8, которые называются аксиомами векторного пространства.

Проекция вектора на ось

Определение. Ось – это прямая, на которой выбрано направление, заданное ненулевым вектором.

Алгебраическое значение проекции

Определение. Алгебраическим значением проекции вектора АБ на ось а параллельно прямой l назовем число, равное

Свойства алгебраического значения проекции

Ортогональная проекция

Теорема. Пусть - ортогональная проекция АБ на а. Тогда .

Доказательство.

Линейная зависимость и независимость системы векторов

, k – какое то число.

Х – линейная комбинация векторов.

Если х=0, все равны 0, то назовем систему векторов линейно независимой.

Если существует , при котором х=0, то система линейно зависимая.

Базис векторного пространства (базис системы векторов)

Базисом векторного пространства назовем множество векторов, которое:

1. Базис линейно-независимый.

2. Любой вектор можно представить в виде линейной комбинации векторов из базиса

Базис обозначается как е_{циферка} , где циферка – размерность базиса.

Теорема

Рассмотрим векторное пространство и – его базис. Тогда можно выразить любой вектор через этот базис. Так и только так.

Доказательство

Пусть не только так. (то же самое через у). Все равно потом получим что x=y. Такие дела.

Разложение вектора по базису

Х=х1е1+х2е2+хкек – разложение вектора по базису.

Координаты вектора

X1,x2,xn – координаты вектора x в базисе e1,e2,en

– координатный столбец вектора х

Теорема

При сложении двух векторов соответственные координаты складываются, при умножении на число каждая координата умножается на число

Доказательство

Х=х1е1+х2е2+хкек

Y=y1e1+y2e2+ykek

X+y= (х1е1+х2е2+хкек)+( y1e1+y2e2+ykek), выносим каждое е и профит.

Х*число=число*( х1е1+х2е2+хкек), раскрываем.

Базис множества всех векторов на прямой(GV1)

Любой ненулевой вектор в GV1 образует базис.

Доказательство

Все векторы на прямой коллинеарны друг другу, значит их можно выразить.

Базис множества всех векторов на плоскости (GV2)

Теорема

Пара неколлинеарных векторов образует базис в GV2

Док-во

Пусть есть базис e1,e2; e1,e2 не ноль,

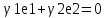
От противного: пусть какое-то альфа не ноль, тогда наш базис линейно независимый.

Базис множества всех векторов в пространстве (GV3)

Теорема

Упорядоченная тройка векторов некомпланарных векторов образует базис в GV3.

Доказательство

Пусть e1,e2,e3 – некомпланарные, каждый не равен 0, тогда:

1. – линейно независимая система

(от противного) Пусть существует какое то гамма не ноль,

2. блаблабла

Скалярное произведение векторов и его свойства

Скалярным произведением векторов а и б назовем число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается а*b=(a;b)

Свойства:

1. 

2. 

3. если , для всех а,б не ноль

4. 

5. 

Доказательство

6. 

Доказательство

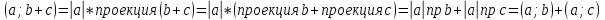
Скалярное произведение в произвольном базисе

Пусть e1,e2,e3 – базис GV3

A=a1,a2,a3

B=b1,b2,b3

Скалярное произведение в ортонормированном базисе

т.к.

Вычисление длины вектора

Угол между векторами

Ортогональный базис

Скалярное произведение любой комбинации векторов оснований базиса равно нулю.

Ортонормированный базис

Базис назовем ортонормированным если он ортогональный и все его векторы равны единице.

Задание ориентации на прямой, на плоскости и в пространстве

1. На прямой (GV1)

Любой не нулевой вектор

2. На плоскости (GV2)

Любые 2 некомпланарных вектора.

Если кратчайший путь от 1 вектора ко второму осуществляется против часовой, то такая ориентация называется положительной, в противном случае – отрицательной.

3. В пространстве (GV3)

Тройку назовем правой, если кратчайший поворот от первого вектора ко второму происходит против часовой.

Векторное произведение векторов

Векторным произведением векторов (a;b) назовем вектор с, который делается следующим образом

1. 

2. – правая тройка

3. 

Обозначается как [a,b].

Если один из векторов равен 0, то все произведение равно 0.

Свойства векторного произведения

1. 

2. 

Доказательство

Ну а синусу на все похер.

3. 

4. [a,b]=0, если a||b, или один из них 0

5. Модуль векторного произведения равна площади параллелограмма, построенного на данных векторах

Смешанное произведение векторов

Смешанным произведением назовем скалярное произведение

Ориентированным объемом параллелепипеда, построенного на а,б,с назовем объем данного параллелепипеда, взятого с плюсом, если тройка правая и с минусом если левая.

Свойства смешанного произведения

1. Смешанное произведение 3х векторов равно ориентированному объему параллелепипеда, построенного на данных векторах

Док-во

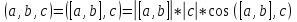, где – площадь основания, а – его высота.

2. 

3. Логический сдвиг налево

4. При перестановке двух векторов меняется знак

Критерий компланарности трех векторов

3 векторы компланарны, когда их смешанное произведение равно 0.

Векторное произведение в координатах

все одинаковые равны 0, все остальные дают третью букву

Смешанное произведение в координатах

в базисе

Смешанное произведение в произвольном базисе е1, е2, е3