
LEKTsIYa_5
.docЛЕКЦИЯ 5
НЕПРЕРЫВНОСТЬ ФУНКЦИ

Пусть функция
![]() определена в некоторой
области X,
т.х0
принадлежит
определена в некоторой
области X,
т.х0
принадлежит
этой области.
Определение:
Функция
![]() называется непрерывной в т. х0,
если она определена в окрестности этой
точки, включая и х0
и если
называется непрерывной в т. х0,
если она определена в окрестности этой
точки, включая и х0
и если
![]() (1)
(1)
Или, в других
терминах: переход от значения х0
к другому значению х можно представить
так, что значению х0
придано приращение![]() .
Новое значение функции отличается от
старого на приращение
.
Новое значение функции отличается от
старого на приращение
![]() (2)
(2)
Для того, чтобы
![]() была непрерывна в т. х0,
необходимо и достаточно чтобы ее
приращение
была непрерывна в т. х0,
необходимо и достаточно чтобы ее
приращение
![]() в этой точке стремилось к нулю вместе
с приращением
в этой точке стремилось к нулю вместе
с приращением
![]() .
.
![]() (3)
(3)
Или, другими словами:
Определение 2. Бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Еще одна формулировка непрерывности функции.
Определение 3.
Функция
![]() ,
определенная в некоторой окрестности
т.
,
определенная в некоторой окрестности
т.![]() называется
непрерывной в точке
называется
непрерывной в точке
![]() ,
в которой она принимает значение
,
в которой она принимает значение
![]() ,
если, каково бы ни было малое положительное
,
если, каково бы ни было малое положительное
![]() ,
можно указать другое положительное
число
,
можно указать другое положительное
число
![]() ,
выбор которого зависит от выбора
,
выбор которого зависит от выбора
![]() ,
такое, что каждому значению аргумента
х,
взятому из
,
такое, что каждому значению аргумента
х,
взятому из
![]() -окрестности
т.а,
соответствует значение функции в
-окрестности
т.а,
соответствует значение функции в
![]() -
окрестности
-
окрестности
![]() .
.
В некоторых случаях необходимо рассматривать такое изменение аргумента х при котором х стремится к некоторому значению а только с одной стороны, либо монотонно возрастая, т.е. оставаясь все время меньше а (слева от а), либо монотонно убывая, т.е. оставаясь все время больше а (справа от а). Такой характер изменения аргумента условно обозначается с помощью следующих символов:
![]() (4)
(4)
Определение: Если при одностороннем изменении аргумента, функция стремится к определенному пределу, то их называют односторонними пределами функции в т.а (левым пределом и правым пределом в т.а).
![]() (5)
(5)
![]()
Тогда,
а) Если существует
предел функции при
![]()
![]() ,
,
то предел слева будет равен пределу справа:
![]() ,
,
б) Если предел слева равен пределу справа
![]()
То
![]() ,
что означает, что функция
,
что означает, что функция
![]() непрерывна.
непрерывна.
ТЕОРЕМЫ.
-
Если две функции
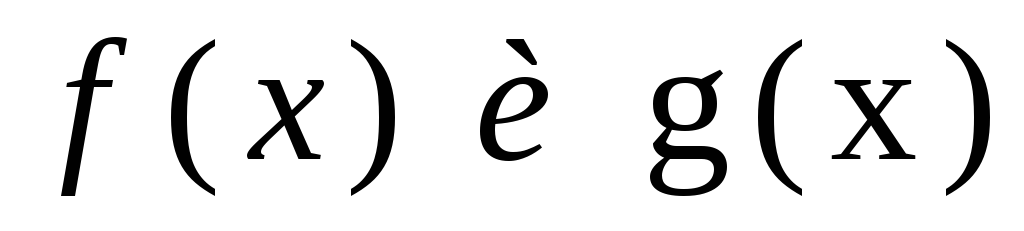 определены в одном и том же промежутке
X
и обе непрерывны в т. х0,
то в этой точке будут непрерывны и
функции:
определены в одном и том же промежутке
X
и обе непрерывны в т. х0,
то в этой точке будут непрерывны и
функции:
![]()
-
Всякая элементарная функция непрерывна в каждой точке, где она определена.
РАЗРЫВ ФУНКЦИЙ
Если в какой-либо
точке
![]() для функции
для функции
![]() не выполняются условия непрерывности
(т.е. или функция в точке не определена,
или пределы слева и справа разные, т.е.
не выполняются условия непрерывности
(т.е. или функция в точке не определена,
или пределы слева и справа разные, т.е.
![]() не
существует), то
не
существует), то
![]() разрывна в точке
разрывна в точке
![]() и т.
и т.
![]() называется точкой разрыва функции.
называется точкой разрыва функции.
Пример 1.
![]()
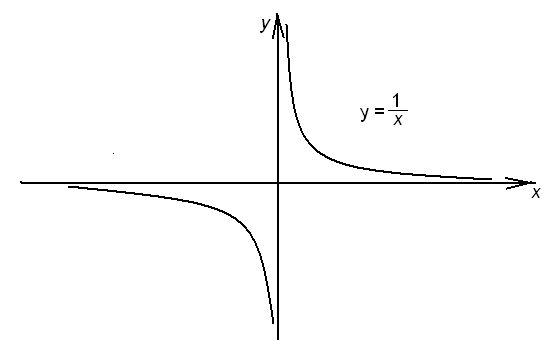 При х=0,
функция у(х)
не
При х=0,
функция у(х)
не
определена.
Пример 2.
![]()

При х=0 функция у(х) не определена
Пример 3.
![]() при х=0
предел функции не существует.
при х=0
предел функции не существует.
ТОЧКИ РАЗРЫВА ФУНКЦИИ
Разрыв первого рода
Точка
![]() разрыва функции называется точкой
разрыва 1 рода если существуют конечные
односторонние пределы функции:
разрыва функции называется точкой
разрыва 1 рода если существуют конечные
односторонние пределы функции:
![]() и (6)
и (6)
![]()
При этом, функция
не обязательно должна быть определена
в т
![]() ,
т.е.
,
т.е.
![]() может и не существовать.
может и не существовать.
Величина
![]() называется скачком функции в т.
называется скачком функции в т.
![]() .
.
Все прочие точки разрыва называются точками разрыва 2 рода.
Если
![]() ,
то точка разрыва функции называется
устранимой.
,
то точка разрыва функции называется
устранимой.
Примеры на разрывы 1 рода
1) 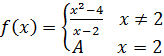
Т ак
как при
ак
как при ![]() функция не существует, то в этой точке
она терпит разрыв. Найдем левый и правый
предел
функция не существует, то в этой точке
она терпит разрыв. Найдем левый и правый
предел
![]()
![]()
то есть разрыв
можно устранить, если взять ![]()
Функция в этом случаи будет непрерывна.
В т. х=2 устранимый разрыв.
2) ![]() , а
= const
, а
= const
![]()
![]()
В т. х=1 разрыв первого рода
3) Исследовать на
непрерывность 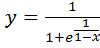
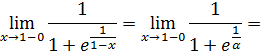
 0
0
![]()
![]()
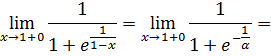 1
1
![]()
В т. х=1 разрыв
первого рода.
Скачок
![]()
4) 
функция неопределенна
и непрерывна на числовой оси, кроме ![]() .
Исследуем точку разрыва функции:
.
Исследуем точку разрыва функции:
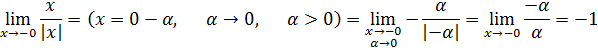

![]() скачок
скачок
![]()
![]()
В т. х=0 разрыв первого рода.
5 )
)
![]()
![]()
![]()
![]()
В точке ![]() разрыв 1 рода, скачок
разрыв 1 рода, скачок
![]() =
=
Разрыв второго рода
6) ![]()
Область определения
функции
![]() ,
,
![]() ,
,
![]()
В
интервале ![]() функция не
функция не
определена, однако, точками ее разрыва
является
только граничные точки ![]() и
и
![]() .
В этих точках функция не определена, но
.
В этих точках функция не определена, но
она определяется в сколь угодно близких точках
слева
от ![]() и справа от
и справа от ![]()
![]()
![]()
в точках х = -3 и х =0, разрыв второго рода, справа и слева от точек разрыва функция непрерывна
7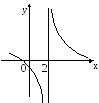 )
)
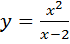
![]()
![]()
![]()
![]()
![]()
в точке х = 2, разрыв второго рода, справа и слева от точек разрыва функция непрерывна.
8) ![]()
![]()

![]()
![]()
в точке ![]() ,
-разрыв
второго рода,
справа и слева от точек разрыва функция
непрерывна.
,
-разрыв
второго рода,
справа и слева от точек разрыва функция
непрерывна.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Производная. Механический и геометрический смысл
Пусть функция![]() определена в промежутке Х.
Дадим ей некоторое приращение
определена в промежутке Х.
Дадим ей некоторое приращение
![]() ,
такое, что
,
такое, что
![]() не выходит из области Х.
не выходит из области Х.
Определение:
Производной
![]() или
или
![]() от данной функции
от данной функции
![]() называется предел отношения приращения
функции к приращению аргумента, при
условии, что приращение аргумента
стремится к нулю.
называется предел отношения приращения
функции к приращению аргумента, при
условии, что приращение аргумента
стремится к нулю.
![]() или
или
![]() ;
;
![]()
Найти производную функции
![]()
![]()
![]()
![]()
![]()
Механический смысл
Пусть задан закон
движения материальной точки
![]() .
Требуется определить скорость движения
в момент времени
.
Требуется определить скорость движения
в момент времени
![]() .
.
По закону движения
![]() в момент времени
в момент времени
![]() мы имеем
мы имеем
![]() .
Через промежуток времени
.
Через промежуток времени
![]() имеем время
имеем время
![]() ,
а путь
,
а путь
![]()
Т.е. за промежуток
времени
![]() точка прошла путь
точка прошла путь
![]() .
.
Тогда, средняя скорость движения будет
![]()
Для нахождения
скорости в момент времени
![]() находят
предел средней скорости за бесконечно
малый промежуток времени
находят
предел средней скорости за бесконечно
малый промежуток времени
![]() .
.
![]() и ли
и ли
![]()
Т.о. скорость неравномерного движения в каждый данный момент времени равна производной от пути по времени – это механический смысл производной.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
 Дана функция
Дана функция
![]() .
Найдем
.
Найдем
уравнение касательной к графику
функции в произвольной точке
![]() .
Построим касательную в
.
Построим касательную в
этой точке. Возьмем соседнюю к
точке М точку
![]() .
Проведем
.
Проведем
через точки М0 и М1 секущую до пересечения с осью ох. Обозначим
угол между секущей
и осью ох за
![]() .
Обозначим за
.
Обозначим за
![]()
![]() .
Устремим т. М1
к т. М0,
двигаясь по кривой
.
Устремим т. М1
к т. М0,
двигаясь по кривой
![]() .
Тогда
.
Тогда
![]() ,
а угол
,
а угол
![]() .
Секущая М0М1
стремится занять положение касательной,
проходящей через т.М0.
.
Секущая М0М1
стремится занять положение касательной,
проходящей через т.М0.
Т.е. касательной
к кривой в т.М0
называется предельное положение секущей
М0М1
при стремлении т.М1
к т. М0.
Угловой коэффициент секущей:
![]() .
Угловой коэффициент касательной получим
как:
.
Угловой коэффициент касательной получим
как:
![]() ,
т.е.
,
т.е.
![]() равен производной функции
равен производной функции
![]() в т.х0.
в т.х0.
Уравнение касательной:
![]()
Т.о., геометрический смысл производной - производная это тангенс угла наклона касательной к данной кривой в данной точке.
Пример. Найти тангенс угла наклона касательной к кривой у = х2 в
т.М (1/2, ¼).
![]()
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ
По определению
![]()
Определение: функция, имеющая в данной точке х =х0 производную, называется дифференцируемой в этой точке; функция, имеющая производную во всех точках некоторого промежутка (а,в) называется дифференцируемой в этом промежутке.
Пусть
![]() дифференцируема в т.х0
и ее производная
дифференцируема в т.х0
и ее производная
![]() ,
тогда
,
тогда
![]()
Т.к. переменная величина, имеющая предел может быть представлена в виде суммы предела и б.м. величины, то
![]() ,
,
Умножим на
![]() ,
,
![]() при
при
![]() ,
что и означает, что функция
,
что и означает, что функция
![]() непрерывна.
непрерывна.
Однако, непрерывность не является достаточным условием дифференцирования.
Из отношения двух
б.м. мы знаем, что![]() может
не существовать. Это будет в случае,
если в определенной точке функция не
будет иметь определенной касательной,
либо, угол наклона касательной равен
может
не существовать. Это будет в случае,
если в определенной точке функция не
будет иметь определенной касательной,
либо, угол наклона касательной равен
![]() .
.
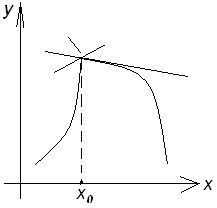

Т.о. не всякая непрерывная функция дифференцируема, но всякая дифференцируемая непрерывна.
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Правила отыскания производной в точке называется дифференцированием.
-
Производная от аргумента
Полагая
у
= х,
находим
![]()
Поэтому
![]()
![]()
т.е.
![]()
-
Производная от постоянной
Пусть у
= с,
тогда,
![]() ,
поэтому, при всяком
,
поэтому, при всяком
![]()
Имеем
![]() ,
тогда
,
тогда
![]() ,
т.е.
,
т.е.
![]()
-
Производная суммы
Докажем, что производная суммы функций равна сумме их производных
Пусть у
= u
+ v,
![]() ,
,
![]()
Отсюда, переходя
к пределу, при
![]() имеем
имеем
![]()
![]()
-
Производная произведения
Найдем производную произведения двух функций
у = u v
![]()
![]()
Делим на
![]()
![]()
u
и v
здесь const,
а
![]() -
переменные.
-
переменные.
Перейдем к пределу
при
![]()
![]()
Таким образом
![]()
Примечание:
![]() ,
т.к. v
являясь
дифференцируемой функцией аргумента
х, является функцией непрерывной, а для
непрерывной функции
,
т.к. v
являясь
дифференцируемой функцией аргумента
х, является функцией непрерывной, а для
непрерывной функции
![]()
-
Постоянный множитель можно выносить за знак производной.
y = cu
![]() ,
c = const
,
c = const
![]()
-
Производная частного
Пусть
![]() ,
где u
и v
– дифференцируемые функции.
,
где u
и v
– дифференцируемые функции.
![]()
![]()
Делим на
![]() (
при
(
при
![]() )
)
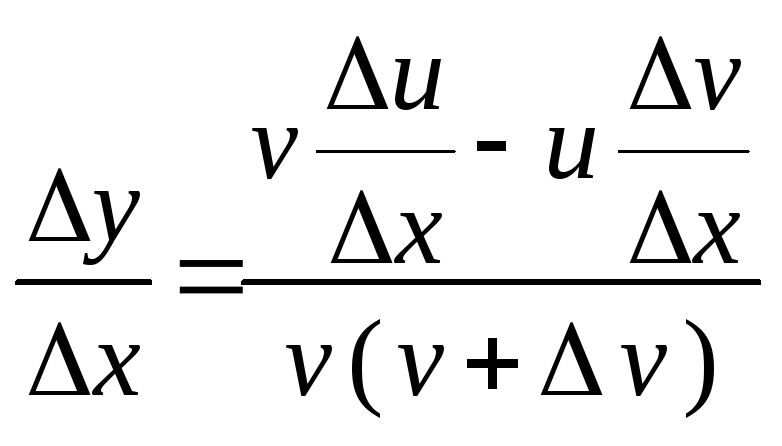 перейдем к пределу
при
перейдем к пределу
при
![]()
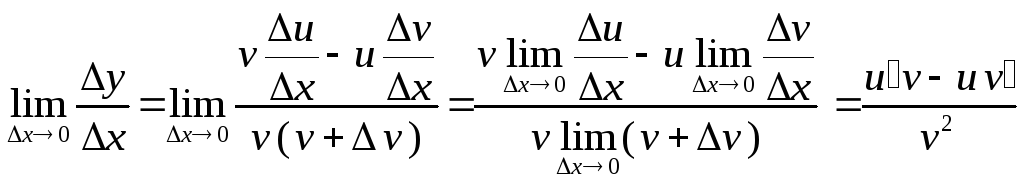
Пояснение:
![]()
Получили:
![]()
Если u
= C, то
![]() ,
тогда имеем
,
тогда имеем
![]() ,
,
При с = 1, имеем
![]()
