Лекции 6

Типичные задачи линейного программирования

Задача №1 (об использовании ресурсов).

Для осуществления n различных процессов Т_j, j=1..n, требуется m видов ресурсов S_i, i=1..m, запасы которых ограничены и равны b_i, i=1..m. Известен расход ресурсов S_i на каждую единицу процесса Т_j в виде матрицы значений а_ij и доход от реализации единицы продукции Т_j в виде вектора с_j. Требуется найти распределение процессов Т_j, при котором доход будет максимальным.

Решение. Пусть х_j, j=1…n, распределение процессов (количество единиц продукции), W – доход. Тогда W = c_j x_j - целевая функция.

Система ограничений – неравенств:

a_ij x_j ≤ b_j i =1…m, которая переводится в систему равенств введением переменных x_n+i, i=1…m, означающих не использованные ресурсы S_i.

Получаем: a_ijx_j + x_n+i = b_i , i=1…m.

Начальное решение x_j = 0, j = 1…n, базисные переменные x_n+j = b_i , i = 1…m. Решается задача максимума целевой функции W.

Замечание. Если есть ограничения в виде неравенства «больше или равно», то используем двух этапный симплекс - метод.

Пусть имеется дополнительно k неравенств

a_ij x_j ≥ b_i , i = (m +1)…(m + k).

Вводятся по 2 дополнительные переменные

x_m+n+i и x_m+n+k+i , i = 1…k,

а неравенства представляются в виде следующих уравнений:

a_{i +m,j} x_j – x_m+n+i +x_m+n+k+i = b_m+i , i = 1…k.

Начальное решение x_j = 0, j =1…n, x_m+n+i = 0, i = 1…k, базисные переменные x_i+n , i =1…m, x_m+n+k+i , i = 1…k.

Целевая функция первого этапа x_n+m+k+i, необходимо найти минимум .

После первого этапа решения обращается в ноль и находится начальное решение для второго этапа, при этом x_n+m+k+i = 0 для всех i = 1…k. Если этого не получится, то требования противоречивы.

При решении второго этапа искусственные переменные x_n+m+k+i не рассматриваются.

Задача №2 (о распределении выпуска изделий).

За время Т необходимо изготовить m видов продукции А_i, i=1..m, в количестве N_i каждое.

Эти виды продукции выпускаются на n предприятиях (цехах, станках и т.д.) П_j, j=1..n. Известно а_ij количество продукции А_i, выпускаемое на предприятии П_j за единицу времени, b_ij – стоимость единицы продукции А_i, выпущенное на предприятии П_j. Требуется найти x_ij – время работы предприятия П_j над продукцией А_i (одновременно на предприятии может выпускаться только один вид продукции), при котором стоимость выпускаемой продукции будет минимальной.

Решение.

Ограничения:

1. Время работы каждого предприятия не может превышать Т.

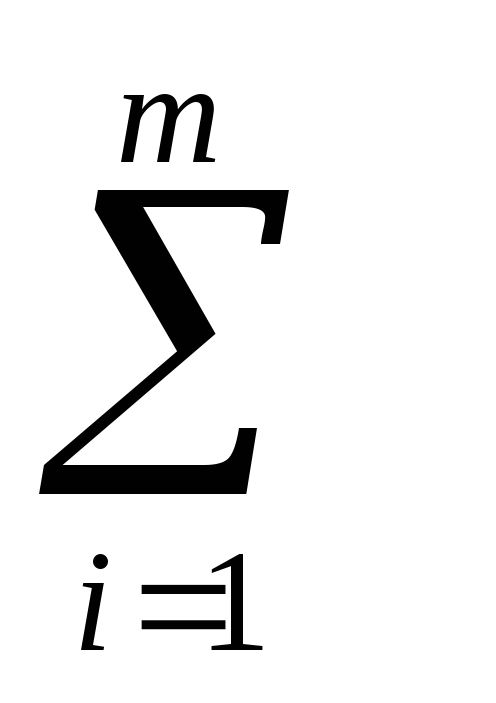x_ij ≤Т , j =1…n.

2. Количество выпускаемой продукции должно соответствовать номенклатуре

a_ij x_ij =N_i , i = 1…m.

Целевая функция – общая стоимость выпускаемой продукции

W = a_ij b_ij x_ij - должна быть минимальной.

Вводим дополнительные переменные и записываем неравенства в виде равенств:

x_{i j} + y_j = Т, j=1…n. Дополнительные переменные y_j означают время простоя предприятия П_j.

Во второе ограничение вводим искусственные переменные y_j .

a_ij x_ij + y_n+i = N_i , i = 1…m (y_n+i – искусственные переменные).

Необходимо использовать двухэтапный симплекс-метод.

Этап1. Ищется минимум y_n+i , и добиваются, чтобы y_n+i = 0 при всех i = 1…m.

Этап2. Потом решается основная задача: ищется минимум целевой функции

W= a_ijb_ijx_ij.

Задача №3 (транспортная задача).

В пунктах Р_i имеется однородный груз в количестве а_i, i=1..m. Его необходимо перевести в пункты Q_i в количестве b_j, j=1..n, так чтобы стоимость перевозок была минимальна. При этом количество требуемого груза равно имеющимся запасам . Известна c_ij – стоимость перевозки единицы груза из Р_i в Q_i.

Решение. Пусть х_ij – количество груза, перевозимого из Р_i в Q_j.

Ограничения:

1. Количество груза из P_i на все пункты должно быть равно имеющимся запасам

x_ij = a_i , i =1…m

2. Количество груза, пребываемого в Q_j со всех пунктов, равно потребностям

x_ij = b_j , j = 1…n.

Целевая функция W =c_ij x_ij, требуется найти её минимум.

P.S. Если груз превышает потребности, вводится фиктивный пункт Q_n+1 , на которую переводится остаток груза b_n+1 со стоимостью перевозок c_i,n+1 = 0.

Для решения можно ввести искусственные переменные y_i и z_j, тогда

x_ij + y_i = a_i , i = 1…m,

x_ij + z_j = b_j , j = 1…n.

На первом этапе минимизируем y _i + z_j. После того, как все y_i и z_j будут равны нулю, находим допустимое базисное решение. Далее (на втором этапе) находим минимум основной целевой функции W.

А можно системы уравнений

x_ij = a_i и x_ij = b_j , i =1…m , j =1…n,

преобразовать так, что бы х_ij – входили в уравнения по одному разу с коэффициентом +1. Это избавит нас от введения искусственных переменных y_i и z_i и позволит использовать одноэтапный симплекс-метод.

Задача №4 (о выборе оптимального варианта аппаратуры).

Требуется спроектировать устройство, состоящее из m последовательных блоков (i = 1…m). Имеется n различных вариантов выполнения каждого модуля

(j = 1…n). Заданы ограничения в виде максимальной стоимости (X), габаритов (Y) и максимального времени производства операций (z).

Требуется выбрать оптимальный вариант.

Пусть x_{i ,} y_i, z_i – стоимость, габариты и время операций для каждого блока.

x_i ≤X, y_i ≤Y, z_i ≤Z,причем x_i{ x_i1…x_in}, y_i {y_i1…y_in}, z_i{z_i1…z_in}, где x_ij , y_ij , z_ij – стоимость, габариты, время операций i - блока при j –ом варианте его исполнения.

Пусть c₁, c₂, c₃ – коэффициенты, характеризующую относительную ценность уменьшение стоимости, габаритов и времени.

Целевую функцию W = с₁ x_i + c₂ y_i + c₃z_i необходимо сделать минимальной.

Т.к. x_i, y_i, z_i могут принимать только дискретные значения из {x_i1…x_in}, {y_i1…y_in}, {z_i1… z_in}, то задача решается методами дискретного программирования.

28