ПлИзмЭкс_Курсовик_1

I. Проведен эксперимент по определению зависимости Y=f(x), результаты которого сведены в таблицу 1.

Таблица 1.

		m=7
	x	0,2	0,6	1	1,4	1,8	2,2	2,6
n=6	Y1	7,21	7,2	9,19	11,15	16,94	26,01	39,03
	Y2	7,36	7,76	8,32	12,49	18,64	25,17	38,18
	Y3	8,5	8,08	8,27	12,41	18,36	25,51	36,75
	Y4	7,06	6,33	8,67	11,48	17,59	25,61	36,77
	Y5	8,04	9,19	9,13	13,32	18,47	25,71	38,31
	Y6	8,24	7,57	8,03	12,07	17,88	26,37	38,03
	Yi	7,735	7,688	8,602	12,153	17,98	25,063	37,845
		0,361	0,902	0,229	0,601	0,413	3,1916	0,824

Найти уравнение регрессии по экспериментальным данным и провести анализ полученной модели. Доверительную вероятность принять равной P=0.95.

Графическое представление экспериментальных данных по определению зависимости Y=f(x)

Рис.1(точки – значения Y; звездочки – Yi)

Рассчитаем Yi –среднее значение Y для каждого значения x, по формуле и полученные данные занесем в таблицу 1:

Рассчитаем оценку дисперсий случайной составляющей для области значений при каждом Xi , по формуле и полученные значения занесем в таблицу:

Проверим полученные оценки дисперсий на однородность. т.к. ni=n проверку будем проводить по критериям Кохрена.

G=0,2575 < Gp(5,7)=0,3974

из полученного неравенства следует что оценки дисперсий однородны. И за оценку дисперсии случайной составляющей можно взять среднее значение дисперсий по формуле :

Тогда оценка дисперсии случайной составляющей средних Yi равна:

X=Xi+1-Xi то можно перевести зависимость Y(X) к зависимости Y(z) тогда уравнение регрессии: 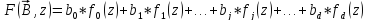будет ортогональным полиномом.

Формула перехода x к z:

Таблица 2

x	0.2	0.6	1	1.4	1.8	2.2	2.6
z	1	2	3	4	5	6	7

Уравнение регрессии: ортогональный полином 0-порядка.

Уравнение ортогонального полинома 0-порядка имеет вид F0(z)=f₀(z)*b₀

Где f₀(z)=1

Коэффициент b₀ находим поформуле:

Проведем проверку значимости коэффициента b₀ по формуле:

Где - оценка дисперсии коэффициента b₀

1,4112*10^3 > 2,4469

Значит коэффициент b₀ – значим.

Тогда F0(z)= f₀(z)*b0=16.819 график функции представлен на рис.2

Рис 2.

Рассчитаем выборочную оценку дисперсии уравнения F0(z) по формуле:

где l₁=1 ;

Проверим адекватность выбранной модели с помощью критерия Фишера.

F=1554.3 > 2.37=Fp(6;35)

Из неравенства следует что выбранная модель не адекватна. Добавим в уравнение регрессии следующую составляющую.

Уравнение регрессии: ортогональный полином 1-порядка.

Уравнение ортогонального полинома 1-порядка имеет вид F1(z)=f₀(z)*b₀+ f₁(z)*b₁

Где ;

Коэффициент b₁ находим по формуле: ;

Проведем проверку значимости коэффициента b₀ по формуле:

1627 > 2,4469

Где - оценка дисперсии коэффициента b₁

Значит коэффициент b₁ – значим.

Тогда F₁(z)=f₀(z)*b₀+f₁(z)*b₁ график функции представлен на рис.3

Таблица 3

z	1	2	3	4	5	6	7
f1(z)	-3	-2	-1	0	1	2	3
F1(z)	2.2699	7.1196	11.9693	16.819	21.6688	26.5185	31.3682

Рис.3

Рассчитаем выборочную оценку дисперсии уравнения F1(z) по формуле:

где l₂=2;

Проверим адекватность выбранной модели с помощью критерия Фишера.

F=286,4243 > 2.48=Fp(5;35)

Из неравенства следует что выбранная модель не адекватна.

Добавим в уравнение регрессии следующую составляющую.

Уравнение регрессии: ортогональный полином 2-порядка.

Уравнение ортогонального полинома 2-порядка имеет вид F2(z)=f₀(z)*b₀+ f₁(z)*b₁+ f₂(z)*b₂

Где f₂(z) рассчитываем по формуле:;

Тогда ;

Коэффициент b₂ находим по формуле: ;

Проведем проверку значимости коэффициента b₂ по формуле:

1193 > 2,4469

Где - оценка дисперсии коэффициента b₂

Тогда F₂(z)=f₀(z)*b₀+f₁(z)*b₁+ f₂(z)*b₂ график функции представлен на рис.4

Таблица 4

z	1	2	3	4	5	6	7
f2(z)	5	0	-3	-4	-3	0	5
F2(z)	8.195	7.1196	8.4143	12.079	18.1137	26.5185	37.2933

Рис.4

Рассчитаем выборочную оценку дисперсии уравнения F2(z) по формуле:

где l₃=3;

Проверим адекватность выбранной модели с помощью критерия Фишера.

F=4.5538 < 2.64=Fp(4;35)

Из неравенства следует что выбранная модель не адекватна. Добавим в уравнение регрессии следующую составляющую.

Уравнение регрессии: ортогональный полином 3-порядка.

Уравнение ортогонального полинома 3-порядка имеет вид F3(z)=f₀(z)*b₀+ f₁(z)*b₁+ f₂(z)*b₂+ +f₃(z)*b₃

Где f₃(z) рассчитываем по формуле:;

Тогда ;

Коэффициент b₃ находим по формуле: ;

Проведем проверку значимости коэффициента b₃ по формуле:

193,4611 > 2,4469

Где - оценка дисперсии коэффициента b₃

Тогда F₃(z)=f₀(z)*b₀+f₁(z)*b₁+ f₂(z)*b₂ +f₃(z)*b₃ график функции представлен на рис.4

Таблица 4

z	1	2	3	4	5	6	7
f3(z)	-6	6	6	0	-6	-6	6
F3(z)	7.747	7.568	8.8626	12.079	17.6654	26.0701	37.7416

Рис.5

Рассчитаем выборочную оценку дисперсии уравнения F3(z) по формуле:

где l₄=4;

Проверим адекватность выбранной модели с помощью критерия Фишера.

F=6,4*10^-28 < 2.87=Fp(3;35)

Неравенство показывает адекватность выбранной модели:F(z)=f₀(z)*b₀+f₁(z)*b₁+ f₂(z)*b₂+ +f₃(z)*b₃;

Оценка точности полученных результатов.

Оценка дисперсии полученной модели F(z) равна:

Функция верхней границы доверительного интервала:

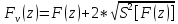
Функция нижней границы доверительного интервала:

Перейдем обратно от Z к X и получим адекватное уравнение регрессии зависимости Y=f(x)

Рис.6

II. 1. Проведен полный факторный эксперимент ПФЭ типа 2² в диапазоне факторов, указанных в таблице и получены следующие результаты измерений

Таблица 5

Ni	t(0C)	U(B)	Y1	Y2	Y3	Y4	Y5
1	-20	210	15.82	16.83	15.89	16.18	17.17
2	20	210	9.37	8.92	8.84	9.9	9.64
3	-20	230	10.98	10.27	10.96	10.62	11.24
4	20	230	23.56	23.37	23.5	23	24.07

Определить уравнение поверхности отклика и провести анализ полученной модели.

Доверительную вероятность принять равной P=0,95

2. По результатам п.1 построить симплекс эксперимент для основных переменных.

Считать точность определения Y одинаковой.

3. Дать сравнительную характеристику моделям, получаемым в п.1 и 2.

Представим поверхность 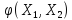многомерным рядом Тейлора:

Часто используют линейные планы т.е. dX_n не в степени.

1. Полный Факторный Эксперимент

Проведем операции центрирования и нормирования поверхности отклика.

т.е. центральную точку поверхности отклика переносим в начало координат и вводим новые единицы:

И в результате получим ортогональные функции.

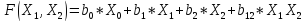
Где

Построим матрицу реализации базисных функций (матрицу Адамара)

Таблица 6

Ni	X0	X1	X2	X1X2	Y1	Y2	Y3	Y4	Y5	Yi
1	+1	-1	-1	+1	15.82	16.83	15.89	16.18	17.17	16.378	0.3551
2	+1	+1	-1	-1	9.37	8.92	8.84	9.9	9.64	9.334	0.2077
3	+1	-1	+1	-1	10.98	10.27	10.96	10.62	11.24	10.814	0.141
4	+1	+1	+1	+1	23.56	23.37	23.5	23	24.07	23.5	0.1488

Рассчитаем Yi –среднее значение Y по формуле и полученные данные занесем в таблицу 6:

Рассчитаем оценку дисперсий случайной составляющей для области значений по формуле и полученные значения занесем в таблицу 6:

Проверим полученные оценки дисперсий на однородность. т.к. ni=n проверку будем проводить по критериям Кохрена.

G=0,4165 < Gp(4,4)=0,6287

из полученного неравенства следует что оценки дисперсий однородны. И за оценку дисперсии случайной составляющей можно взять среднее значение дисперсий по формуле :

Тогда оценка дисперсии случайной составляющей средних Yi равна:

Найдем коэффициенты 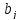по формуле:

Результаты расчета коэффициентов занесем в таблицу 7

Таблица 7

b0	b1	b2	b12
15.0065	1.4105	2.1505	4.9325

Рассчитаем оценку дисперсии для коэффициентов по формуле:

По формуле можно заметить что

Построим поверхность отклика

Рис.7

Поверхность отклика повернутая на 90⁰ влево(рис.8)

Рис.8

Оценка точности полученных результатов.

Оценка дисперсии полученной модели F(X₁,X₂) равна:

Функция верхней границы доверительного интервала:

Функция нижней границы доверительного интервала:

Рис.9

Поверхность отклика повернутая на 90⁰ влево(рис.10)

Рис.10

2. Симплекс эксперимент 2²

Насыщенный эксперимент для нахождения усеченной зависимости.

Число экспериментов равно: N=n+1=3

Точность определения Y такая же как и в ПФЭ.

Нам так же понадобиться значение Y при t=0 и U=230 ; т.е. при X₁=0 и X₂=1

Которое мы возьмем из поверхности отклика предыдущего пункта.

Построим матрицу адамара для симплекс плана:

Таблица 8

Ni	X0	X1	X2	Yi
1	1	-1	-2	16.378	0.0426
2	1	+1	-2	9.334
3	1	0	+22	17.16

Одним из условий нахождений  , мы принимаем что ;

т.е. и

рассчитаем коэффициенты :

Рассчитаем оценку дисперсии для коэффициентов по формуле:

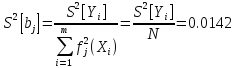
По формуле можно заметить, что

Построим поверхность отклика

Рис.11

Поверхность отклика повернутая на 90⁰ влево(рис.12)

Рис.12

Оценка точности полученных результатов.

Оценка дисперсии полученной модели F(X₁,X₂) равна:

Функция верхней границы доверительного интервала:

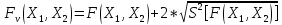
Функция нижней границы доверительного интервала:

Рис.13

Поверхность отклика повернутая на 90⁰ влево(рис.12)

Рис.14

Анализируя результаты полученные в п.1 и п.2 становиться очевидно что ПФЭ дает полную картину поверхности отклика, учитывает все влияющие составляющие поверхности отклика, но в тоже время требует большое количество экспериментов. Число которых сильно растет с увеличением числа факторов. С другой стороны симплекс эксперимент позволяет получить картину поверхности отклика с меньшим количеством экспериментов, но мы получаем усеченную поверхность и теряем составляющие совместных производных факторов( в моем случае отвечающих за так называемою проперлерность поверхности).

Из ходя из того что в конкретном случае двухфакторного анализа (вычисления по которому приведены выше) разница в количестве экспериментов между ПФЭ и Симплекс экспериментом незначительна то плюсы симплекс эксперимента теряют свою значимость из чего следует что при малом числе факторов для анализа поверхности отклика рекомендуется использовать ПФЭ.

Санкт-Петербург

2014г.