сигналы3

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) (СПбГЭТУ)

Кафедра ВТ

РЕФЕРАТ

по дисциплине: «Цифровая обработка сигналов»

на тему: «Линейные дискретные системы с постоянными параметрами»

Выполнил:

Проверил:

г. Санкт-Петербург, 2014 г.

Оглавление

1. Введение 3

2. ЛПП система и ее свойства 4

3. Линейные разностные уравнения 6

4. Частотная характеристика 9

5. Z-преобразование 11

6. Литература 12

Введение

Под дискретной системой понимают техническое устройство или программу, которая осуществляет преобразование дискретной последовательности x(n) в другую дискретную последовательность y(n) в соответствии с заданным алгоритмом.

Рис. – представление дискретной системы

Алгоритм преобразования входной последовательности x(n) в выходную последовательность y(n) описывается соотношением

,

где, , – операторы.

По виду оператора R дискретные системы делят:

• на линейные или нелинейные;

• стационарные или нестационарные;

• физически реализуемые (каузальные) или нереализуемые (некаузальные).

ЛПП система и ее свойства

Дискретная система по существу является алгоритмом преобразования одной последовательности (называемой входной) в другую (называемую выходной). Входная последовательность обозначена через x(n), а выходная — через y(n). Функционально они связаны соотношением

y(n) = ϕ[x(n)]

где вид оператора ϕ() зависит от свойств конкретной системы.

Линейная система определяется следующим образом. Если — некоторые входные последовательности, а 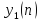и — соответствующие им отклики линейной системы, то при подаче на вход последовательности на выходе образуется последовательность  (a и b — произвольные постоянные).

Система с постоянными параметрами характеризуется тем, что если входной последовательности x(n) соответствует выходная последовательность y(n), то входной последовательности x(n-) при любых  соответствует на выходе последовательность y(n-).

Покажем теперь, что в линейной системе с постоянными параметрами входная и выходная последовательности связаны соотношением типа свертки. Допустим, что x(n) — входная, а y(n) — выходная последовательности ЛПП-системы, и пусть h(n) — отклик системы на единичный импульс, [Последовательность h(n) называют импульсной характеристикой системы или откликом на единичный отсчет.] Используя формулу представления произвольных последовательностей

{a(n)} =

Где а(n) – величина n-ого элемента.

, x(n) можно записать в виде

x(n) =

Рис – представление дискретной системы

Рис – представление линейной системы с постоянными параметрами

Поскольку h(n) является откликом системы на после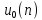довательность  , а параметры системы постоянны, h(n-m) будет откликом на последовательность   . Из свойства линейности следует, что откликом на последовательность x(m) должна быть последовательность x(m)h(n-m). Поэтому отклик на x(n) будет равен

y(n) = (1)

Он имеет вид свертки, что и требовалось доказать. Простой заменой переменных равенство (1) может быть преобразовано к  виду

y(n) =

Таким образом, последовательность h(n) полностью описывает ЛПП-систему, что отображено на рисунках выше.

На рисунке ниже показано, как процесс вычисления свертки осуществляется на практике. А - изображена входная последовательность x(n), отличная от нуля при 0. Б - приведен пример импульсной характеристики h(n), отличной от нуля при  0. в-е - представлены x(m) и h(n-m) для n = 0, 2, 10 и 11. Очевидно, что при n<0 и т>11 последовательности x(m) и h(n-m) не перекрываются y(n) равно нулю. ж - приведена последовательность y(n), являющаяся искомой сверткой.

Свойства линейных систем

1. Порядок установки линейных систем не влияет на выходной сигнал.

2. Любая сложная система будет линейной, если составлена из линейных систем и блоков суммирования.

3. Перемножение сигнала на константу является линейной операцией, а перемножение двух сигналов – нелинейной.

Линейные разностные уравнения

Системы, у которых входная и выходная последовательности x(n) и y(n) связаны линейным разностным уравнением с постоянными коэффициентами, образуют подмножество класса линейных систем с постоянными параметрами. Описание ЛПП-систем разностными уравнениями очень важно, так как оно часто позволяет найти эффективные способы построения таких систем. Более того, по разностному уравнению можно определить многие характеристики рассматриваемой системы, включая собственные частоты и их кратность, порядок системы, частоты, соответствующие нулевому коэффициенту передачи, и т. д.

В самом общем случае линейное разностное уравнение M-го порядка с постоянными коэффициентами, относящееся к физически реализуемой системе, имеет вид

y(n) = (1)

где коэффициенты {} и {} описывают конкретную систему, причем  . Уравнение (1) записано в виде, удобном для решения методом прямой подстановки. Имея набор начальных условий [например, x(i), y(i) для  i=-1,-2,…,-M] и входную последовательность x(n), по формуле (1) можно непосредственно вычислить выходную последовательность y(n) для n. Например, разностное уравнение

y(n) = x(n) – 3y(n-1) (2)

с начальным условием y(-1) =0 и x(n) =   можно решить подстановкой, что дает

y(0) = x(0) – 3y(-1) = 0,

y(1) = x(1) – 3y(0) = 2,

y(2) = x(2) -3y(1) = 0,

y(3) = x(3) -3y(2) = 12,

y(4) = x(4) -3y(3) = -16,

y(5) = x(5) -3y(4) = 78,

y(6) = x(6) -3y(5) = -192,

Хотя решение разностных уравнений прямой подстановкой и целесообразно в некоторых случаях, значительно полезнее получить решение уравнения в явном виде Основная идея сводится к получению двух решений разностного уравнения: однородного и частного. Однородное решение получается путем подстановки нулей вместо всех членов, содержащих элементы входной последовательности x(n), и определения отклика при нулевой входной последовательности. Именно этот класс решений описывает основные свойства заданной системы. Частное решение получают, подбирая вид последовательности y(n) на выходе при заданной входной последовательности x(n). Для определения произвольных постоянных однородного решения используются начальные условия. В качестве примера решим этим методом уравнение (2). Однородное уравнение имеет вид

y(n) + 3y(n-1) = 0 (3)

Известно, что характеристическими решениями однородных уравнений, соответствующих линейным разностным уравнениям с постоянными коэффициентами, являются решения вида  A.Поэтому, подставив в уравнение (3) A вместо y(n), получим

A

A

Частное решение, соответствующее входной последовательности  x(n) = , попробуем найти в виде

Из уравнения (1) получаем

B

Поскольку коэффициенты при равных степенях n должны совпадать, B,С иDдолжны быть равны

B=, C =

Таким образом, общее решение имеет вид

y(n) = +

Коэффициент A определяется из начального условия y(-1) = 0, откуда A =  и

y(n) = (7)

Выборочная проверка решения (7) при  n показывает полное его совпадение с приведенным выше прямым решением. Очевидное преимущество решения (7) состоит в том, что оно позволяет весьма просто определить y(n) для любого конкретного n= .

рис. - Схема реализации простого разностного уравнения первого порядка.

Важное значение разностных уравнений состоит в том, что они непосредственно определяют способ построения цифровой системы. Так, разностное уравнение первого порядка самого общего вида

y(n) = -

можно реализовать с помощью схемы, изображенной на рисунке выше. Блок «задержка» осуществляет задержку на один отсчет. Рассмотренная форма построения системы, в которой для входной и выходной последовательностей используются раздельные элементы задержки, называется прямой формой 1. Ниже мы обсудим различные методы построения этой и других цифровых систем.

Разностное уравнение второго порядка самого общего вида

y(n) =

Рис - Схема реализации разностного уравнения второго порядка.

может быть реализовано с помощью схемы, приведенной на рисунке. В этой схеме для входной и выходной последовательностей также используются раздельные элементы задержки.

Системы первого и второго порядка могут быть использованы при реализации систем более высокого порядка, так как последние могут быть представлены в виде последовательно или параллельно соединенных систем первого и второго порядка.

Частотная характеристика

В частотной области будет использован специальный класс входных последовательностей, имеющих вид x(n) =  . Класс последовательностей является набором собственных функций ЛПП-систем дискретного времени, т. е. для них выходная последовательность совпадает с входной, умноженной на некоторый комплексный коэффициент, зависящий только от .

Рассмотрим класс входных последовательностей вида

x(n) = ,

Если такая последовательность поступает на вход ЛПП-системы с импульсной характеристикой h(n),то на входе появится последовательность

y(n) =

Таким образом, для выбранного класса входных последовательностей отклик совпадает с входной последовательностью с точностью до комплексного множителя H(), который выражается через импульсную характеристику системы следующим образом:

H()=

Поскольку последовательность вида  функционально эквивалентна дискретизованной синусоиде с частотой , то множитель H() называют частотной характеристикой системы, так как он представляет коэффициент передачи ЛПП-системы для каждого значения .

Рис - Импульсная и частотная характеристики системы первого порядка.

Вычислим в качестве примера частотную характеристику ЛПП-системы с импульсной характеристикой h(n) = . Частотная характеристика имеет вид

H()=

Так как || , то сумма геометрической прогрессии (8) будет равна

H() =

На рисунке выше графически представлены h(n), а также модуль и фаза H() как функции частоты  в диапазоне 0.

Некоторые свойства частотной характеристики. Нетрудно заметить, что частотная характеристика является периодической функцией , причем ее период равен . Эта периодичность связана со спецификой дискретизованного колебания: входная последовательность с частотой () (m=) не отличается от входной последовательности с частотой , т. е.

x(n)=

Поскольку H() — периодическая функция, то для полного описания достаточно задать ее на любом интервале длиной 2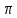. Обычно для этой цели используют интервал  0.

Другим важным свойством частотной характеристики является то, что для действительных h(n) (как обычно и бывает на практике) модуль H() симметричен, а фаза H() антисимметрична на интервале 0. Аналогично действительная часть H() симметрична, а мнимая — антисимметрична на том же интервале. Поэтому при действительных импульсных характеристиках интервал частот, на котором задают частотную характеристику, обычно сокращают до 0.

Z-преобразование

В задачах анализа и синтез линейных дискретных систем широко применяются методы Z-преобразования. Z-преобразование последовательности x(n

T) определяется рядом

где – комплексная переменная. Множество значений z, где ряд сходится, называется областью сходимости.

Z-преобразование обладает рядом важных и широко используемых свойств, непосредственно вытекающих из его определения или легко доказываемых.

1. Линейность. Если последовательности и имеют соответственно Z-преобразования и , и -постоянные, не зависящие от n коэффициенты, то имеет Z-преобразование

2. Сдвиг последовательности. Если и , то имеет Z-преобразование

3. Свертка последовательностей. Пусть и . Свертка последовательностей и

имеет Z-преобразование, равное произведению Z-преобразований исходных последовательностей:

Обратное Z-преобразование

Обратное Z-преобразование ставит в соответствие функции комплексной переменной последовательность , определяемую по формуле

,

где c – контур, расположенный в области сходимости и охватывающий начало координат в z-плоскости. Интеграл удобно вычислять при помощи теоремы о вычетах: функция определяется суммой вычетов подынтегральной функции в полюсах, расположенных в области, охватываемой контуром c:

Литература

1. Цифровая обработка сигналов изображений : учеб. пособие / С.М. Ибатуллин ; Санкт-Петербургский государственный электротехнический университет им. В.И. Ульянова (Ленина) "ЛЭТИ" . - СПб. : Изд-во СПбГЭТУ "ЛЭТИ", 2006.

2. Цифровая обработка сигналов: учеб. пособие для вузов / А.Б.Сергиенко ; - СПб. : Питер, 2002.

3. Алгоритмы и процессоры цифровой обработки сигналов : Учеб. пособие для вузов / А. И. Солонина, Д. А. Улахович, Л. А. Яковлев. - СПб. : БХВ-Петербург, 2001.

4. Цифровая обработка сигналов = Understanding digital signal processing / Р. Лайонс ; пер. с англ. под ред. А. А. Бритова. - 2-е изд. - М. : Бином, 2007.

5. Методические указания к выполнению лабораторных работ по цифровой обработке сигналов. /Сост. Б.А. Курдиков, А.Б. Федотов СПбГЭТУ, 2011г.