Kurpa_Vyshcha_matem_T.1_Gl.5-8_2009

Приклад 2. Побудувати графік функції y lnxx .

1)ОДЗ: x 0 .

2)x 0 – точка розриву функції, тому що

		ln x			ln( 0)				1
	lim									( )	.
		x			0		0		0
	x0

x 0 – вертикальна асимптота (однобічна, тому що x 0 ).

3)Функція загального вигляду, тому що вона визначена на півосі.

4)Функція не періодична.

5)Знайдемо похилі асимптоти y kx b :

1

k lim

f (x)

lim

ln x

lim

x

lim

1

1

0.

x

x

x

x2

x 2x

x 2x2

1

b lim

f (x) kx lim

ln x

lim

x

lim

1

1

0.

x

x

x

x 1

x x

y 0 – горизонтальна асимптота.

6) Знайдемо інтервали монотонності і екстремуми функції.

1

x ln x

y

1 ln x

.

x

x2

x2

296

Знайдемо критичні точки:

y 0 1 ln x 0 ln x 1 x e

y не існує в точці x 0 . Точка x 0 не може бути критичною, тому що в ній функція не визначена.

Критична точка ділить область визначення функції на два інтервали, на кожному з яких перша похідна зберігає знак.

+

max

_

e

0

На інтервалі 0,

e функція

, а на інтервалі e,

функція спадає.

зростає

Точка x e – точка максимуму.

Максимум функції:

y (e)

ln e

1

.

max

e

e

7) Знайдемо інтервали опуклості, угнутості та точки перегину

графіка функції.

1

x2 (1 ln x) 2x

x 2x(1

ln x)

1 ln x

x

y

x4

x4

x2

1 2 2ln x

2ln x 3

.

x3

x3

Знаходимо точки, у яких друга похідна дорівнює 0 або не існує.

3

y 0 2ln x 3 0 ln x 32 x e2 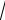ee .

y не існує в точці x 0 . Точка x 0 не може бути абсцисою точки перегину, тому що в ній функція не визначена.

Критична точка x ee ділить область визначення функції на два інтервали, на кожному з яких друга похідна зберігає знак.

_

+

0 ee

297

Графік функції опуклий на інтервалі

0; e

,

тому що на цьому

e

інтервалі

0 ; угнутий

на інтервалі

e

e; ,

тому

що на

цьому

y

інтервалі

0 .

y

При

переході через

точку x e

друга

похідна

змінює

знак,

e

випливає, що ця точка є абсцисою точки перегину графіка функції.

3

Знайдемо ординату точки перегину: y e

ln e

e

e

e

e

3

Точка e

e;

– точка перегину графіка функції.

2e e

8) Знайдемо точки перетинання з осями координат.

y 0

ln x

0 ln x 0 x 1.

x

Точка (1; 0) – точка перетинання з віссю Ox .

1

9)

lim

ln x

lim

x

lim

1

0 ,

тобто при

x

x

x 1

x x

наближується до нуля. Побудуємо графік функції.

		ln e2				3			.
		e	e			2e e

x функція

y

1

e

3

2ee

1	e	e e	x

298

5.4.8. Найбільше і найменше значення функцій на відрізку

Нехай функція y f x

неперервна на сегменті a,b . Тоді, за

теоремою Вейєрштрасса, на цьому відрізку вона досягає свого найбільшого значення і так само свого найменшого значення. Ці значення можуть досягатися на кінцях відрізка або у внутрішніх точках, які є точками екстремуму функції. Звідси випливає така схема відшукання найбільших і найменших значень:

1) Знайти всі критичні точки функції, що лежать усередині відрізка

a,b .

2)Обчислити значення функції в знайдених критичних точках і на кінцях відрізка.

3)Із усіх отриманих значень вибрати найбільше і найменше. Вони й будуть шуканими значеннями, тобто значеннями абсолютного максимуму і мінімуму.

Приклад 1. Визначити найбільше й найменше значення функції

f x x3 3x2 1 на відрізку 1, 4 .

Розв'язання

f x 3x2 6x 3x x 2 . 3x x 2 0 при x 0 й x 2.

Таким чином, дана функція має дві стаціонарні точки x1 0 і x2 2 усередині відрізка 1, 4 . Обчислимо значення функції в цих точках і на

кінцях відрізка:

f 0 1; f 2 3; f 1 3; f 4 17 .

Випливає, найбільшого значення функція набуває на правому кінці відрізка, найменшого – у внутрішній точці х=2 і на лівому кінці відрізка.

За допомогою теорії екстремумів розв’язується багато задач геометричного і фізичного характерів. Припустимо, що задано дві величини, які зв'язані функціональною залежністю, і потрібно відшукати значення однієї з них (укладене в деякому інтервалі, що може бути й необмеженим), при якому інша набуває найменшого або найбільшого значення.

Для розв'язання такої задачі насамперед варто скласти вираз для функції, за допомогою якої одна величина виражається через іншу, а потім знайти найбільше або найменше значення отриманої функції в даному інтервалі.

299

Приклад 2. Які повинні бути розміри циліндра, щоб при даному об'ємі його повна поверхня була найменшою?

Розв’язання. Позначимо через R радіус основи циліндра і через H його висоту. Тоді його повна поверхня

S 2 R2 2 RH .

Оскільки об'єм циліндра заданий, то одна із шуканих величин, наприклад

	H , може бути виражена через R із формули V R2H , звідки			H	V	.
					R2
	Підставляючи цей вираз у формулу для S , одержимо
		V
	S 2 R2		.
		R

Таким чином, S є функцією однієї змінної R , де R 0, . Знайдемо найменше значення цієї функції в даному інтервалі:

dS

V

V

2

2 R

; 2 R

0,

R2

dR

R2

Звідки R 3

V

.

2

Оскільки S при

R 0 і

S при

R та усередині цього

інтервалу маємо лише одну стаціонарну точку, то дійдемо висновку, що при

	R 3	V	повна поверхня S й буде найменшою. При цьому
		2
			H	V	23			V	.
				R2
								2
		Приклад 3. Прямо над центром				круглого майданчика радіуса R

потрібно повісити ліхтар. На якій висоті потрібно це зробити, щоб він якнайкраще освітлював доріжку, яка обмежує майданчик (Степінь освітлення предмета прямо пропорційний косинусу кута падіння променів і обернено

B

пропорційний квадрату відстані предмета від джерела світла).

k cos

Позначимо

степінь освітленості через

Q .

Тоді

Q

AB2

(див. рис.

5.7). Позначимо шукану висоту BC через x .

AC R . Тоді AB2 x2 R2 , cos

BC

x

.

A

С

AB

x2 R2

Рис.5.7

300

Q

kx

x 0, .

Таким чином,

, де

Знайдемо

похідну

від

x2

R2 3 2

утвореної функції

k x2 R2 3 2 kx

3

x2

R2 1 2

2x

k R2 2x2

2

x2 R2 3

x2 R2 5 2 0 .

Q

Звідси знайдемо

x

R

2

. Оскільки при

x 0

і x Q x 0 , а

2

усередині

інтервалу

маємо

єдину

стаціонарну

точку

і

Q x 0 x 0, , то в знайденій точці x

R

2

функція Q x

набуває

2

найбільшого

значення.

Випливає,

ліхтар

треба

повісити на

висоті

BC R 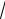2 . 2

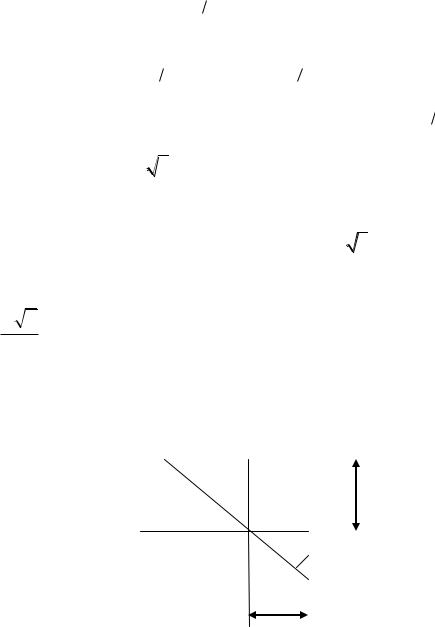
Приклад 4. До ріки шириною a м під прямим кутом побудовано канал шириною b м (рис.5.8.). Якої максимальної довжини кораблі можуть входити в цей канал?

A

M

a

B

N

C

b

Рис. 5.8

Нехай

l AC –

довжина корабля. Позначимо

ACN через

.

Очевидно,

ABM .

Тоді

довжину

корабля AC AB BC можна

знайти, розглядаючи прямокутні трикутники AMB та BNC .

Із трикутника AMB : AB

a

: BC

b

, а із трикутника BNC

.

cos

sin

Випливає, що l

b

a

, де 0

.

sin

cos

2

301

Знайдемо найменше значення функції l( ) на даному інтервалі.

dl

b cos

a sin

0

або bcos3 asin3 0 , звідки знаходимо

d

sin2

cos2

arctg 3

b

.

a

Оскільки при 0

і

l , то при

arctg 3

b

функція

2

a

l( ) набуває мінімального значення, тобто максимально припустима довжина корабля є:

l

b

a

.

b

b

sin arctg 3

cos arctg 3

a

a

a1 3

b

1

cos arctg 3

;

a

b 2 3

a2 3 b2 3

1

a

b1 3

b

sin arctg 3

.

a

a2 3 b2 3

a2 3 b2 3 3 2 .

Тоді l b2 3 a2 3

b2 3

a2 3

a2 3 b2 3

5.5. Елементи диференціальної геометрії

	Диференціал дуги плоскої кривої обчислюється за формулами:
а)	якщо		крива	задана	рівнянням в явному вигляді	y f x ,		тоді
ds 1 f x 2 dx ;
						x t
б)	якщо		крива	задана	параметричними рівняннями		,	тоді
						y t

ds t 2 t 2 dt .

Кривиною кривої називається границя відношення кута суміжності

двох дотичних до нескінченно малої дуги кривої: k lim .

s0 s

302

Під кутом суміжності розуміють кут між дотичними, які проведено в початковій та кінцевій точках дуги M1M2 (рис.5.9).

s	М2
М1
Рис. 5.9
Обчислюється кривина за формулами:

f

а) якщо крива явно задана, то k 1 f 2 3 / 2 ;

б) якщо крива задана параметрично, то k 2 2 3 / 2 .

Радіусом кривини кривої називається величина R 1k .

Центр кривини кривої лежить на нормалі, в бік угнутості кривої, на відстані радіуса кривини від відповідної точки кривої.

Геометричне місце центрів кривини називається еволютою даної кривої. Сама ж крива по відношенню до своєї еволюти називається

евольвентою.

5.6. Фізичні застосування похідної

Значення похідної в даній точці характеризує швидкість зміни функції в цій точці в порівнянні зі швидкістю зростання незалежної похідної. Враховуючи це, можно використовувати поняття похідної при визначенні швидкості різних фізичних процесів.

Приклад 1. Резервуар, який має форму напівкулі з внутрішнім радіусом R(м), заповнюється водою зі швидкістю Q(л) на секунду. Визначити швидкість підвищення рівня води в резервуарі в той момент, коли він буде дорівнювати 0,5 R.

Розв’язання. Позначимо через h рівень води в метрах, а через V її об’єм в м3.

303

Об’єм сегмента кулі: V h2		h
	R		.
		3

Продиференціюємо цю рівність за часом t:

dV

dV

dh

h

1

h2

dh

2Rh h2

dh

2h R

.

dt

dh

dt

3

3

dt

dt

За умовою

dV

0,001Q

м3

.

dt

с

Отже,

dh

0.001Q

м

.

dt

h 2R h

с

При h

R

dh

0,004Q

м

отримаємо

.

3 R2

2

dt

с

Приклад 2. Пліт підтягується до берега за допомогою каната, який намотується на коловорот зі швидкістю 3 м/хв. Визначити швидкість руху плоту в той момент, коли відстань від нього до берега буде дорівнювати 25 м, якщо коловорот розташований на березі вище поверхні води на 4 м.

Розв’язання. Позначимо через S довжину каната між коловоротом та плотом і через x – відстань від плоту до берега, тоді S 2 x2 42 .

Продиференціюємо це співвідношення за часом t:

2S

dS

2x

dx

,

звідки

dx

S

dS

.

dt

dt

dt

x dt

dS

Оскільки

3 ; x 25, то S

252 42 .

dt

Звідки одержуємо

dx

252 42

3 3.03 м/хв.

dt

25

y

Приклад 3.

Драбина довжиною 10 м

одним

кінцем притулена до вертикальної стіни, а іншим

A

спирається на підлогу. Нижній кінець відсувається від

стіни зі

швидкістю

2 м/хв.

З

якою

швидкістю

опускається верхній кінець драбини, починаючи з того

O

B

моменту, коли основа знаходиться на відстані 6 м від

x

стіни? Який напрямок має вектор швидкості?

Рис. 5.8

Розв’язання. Нехай драбина в момент часу t

займає положення AB (рис 27). Відрізок ОВ дорівнює 2t м, довжину АО

304

знайдемо за теоремою Піфагора: AO S t 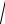100 4t2 , де 0 t 5 .

Закон зміни швидкості опускання верхнього кінця драбини знайдемо як похідну від функції S t .

Нижній кінець драбини буде знаходитися на відстані 6 м від стіни в кінці третьої хвилини. При цьому 3 12 / 8 (м/хв). Знак мінус вказує

на те, що вектор швидкості буде спрямований вертикально вниз.

Приклад 4. Без урахування опору повітря та внутрішнього тертя струмінь води, що витікає з насадки дощувального апарата під кутом до горизонту, рухається за законом

	x 0t cos ,
				(5.9)
		gt	2
	y 0t sin			,
		2
	де 0 – початкова швидкість струменя;		g – прискорення вільного падіння.

Визначити величину швидкості струменя в довільний момент часу t та в момент його удару об землю.

Розв’язання. Вилучимо в струмені води елементарну частинку. Траєкторія її польоту – струмінь, який може бути описаний параметричними рівняннями (5.9). Вектор швидкості руху частинки в довільний момент часу t спрямований по дотичній до траєкторії. Величиниx та y складових вектора швидкості по осях координат Ox та Oy

дорівнюють відповідно похідним від функцій x t та y t за часом t:x xt 0 cos , y yt 0 sin gt .

Величину швидкості руху частинки, а отже, і струменя, в довільний момент часу t знайдемо як геометричну суму величин її складових x та y :

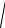2x 2y 0 cos 2 0 sin gt 2 02 2 0 gt sin g2t2 .

Момент удару струменя об землю знайдемо з умови y=0, що дає t0 20 / g sin . Підставляючи знайдене значення t0 у вираз для , знайдемо величину швидкості струменя в момент його удару об землю:

	t0	02 2 0 sin	g 2 0	sin	g 2 4 02 sin2
			g		g 2

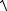
02 402 sin2 402 sin2 0 .

305