EP / Теория ЭП Драчев

ɗɥɟɤɬɪɨɦɚɝɧɢɬɧɵɣ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɩɨɥɭɱɢɦ ɩɨ ɮɨɪɦɭɥɟ

P

3

Ic 2

rc

/s 3 Ic 2

rc

/Įs

M

ɗɆ

2

2

2

2

.

(3.81)

Ȧ0

Į Ȧ0ɇ

Ȧ0ɇ

ɉɪɢ I1 = const ɩɨ ɡɚɤɨɧɭ ɪɚɡɞɟɥɟɧɢɹ ɬɨɤɨɜ ɜ ɩɚɪɚɥɥɟɥɶɧɵɯ ɰɟɩɹɯ ɧɚɣɞɟɦ ɬɨɤ ɪɨɬɨɪɚ

Ic2		I1 xμ
	r2c /Ds 2 xc2 xμ 2				(3.82)
ɢ ɩɨɞɫɬɚɜɢɦ ɜ ɮɨɪɦɭɥɭ ɦɨɦɟɧɬɚ
	3 I2	x2	rc /Ds
M	1	μ	2	.	(3.83)
	Ȧ0ɇ [ r2c /Ds 2 xc2 xμ 2 ]
ɉɪɢ Įs 0 ɢ ɩɪɢ Įs	f ɦɨɦɟɧɬ ɫɬɪɟɦɢɬɫɹ ɤ ɧɭɥɸ Ɇ				0. Ⱦɚɧɧɚɹ ɮɭɧɤɰɢɹ

ɢɦɟɟɬ ɷɤɫɬɪɟɦɭɦ, ɩɨɷɬɨɦɭ ɬɪɟɛɭɟɬɫɹ ɜɡɹɬɶ ɩɪɨɢɡɜɨɞɧɭɸ dM / d(Įs) ɢ ɩɪɢɪɚɜɧɹɬɶ ɟɟ ɧɭɥɸ. ɇɟ ɩɪɢɜɨɞɹ ɩɪɨɦɟɠɭɬɨɱɧɵɯ ɜɵɜɨɞɨɜ (ɫɬɭɞɟɧɬ ɦɨɠɟɬ ɜɵɩɨɥɧɢɬɶ ɢɯ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨ – ɩɨ ɚɧɚɥɨɝɢɢ ɫ ɜɵɜɨɞɨɦ ɜ ɩ. 3.5.2), ɩɪɢɜɟɞɟɦ ɮɨɪɦɭɥɭ ɤɪɢɬɢɱɟɫɤɨɝɨ ɫɤɨɥɶɠɟɧɢɹ

	ĮsɄɌ	r		r2c	,	(3.84)
			xc2	xμ

ɩɪɢ ɤɨɬɨɪɨɦ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɞɨɫɬɢɝɚɟɬ ɦɚɤɫɢɦɚɥɶɧɨɝɨ (ɤɪɢɬɢɱɟɫɤɨɝɨ) ɡɧɚɱɟɧɢɹ:

			3 I2	x2
	MɄɌ		1		μ	.	(3.85)
		2	Ȧ0ɇ (xc2		xμ )

ɉɪɢɜɟɞɟɦ ɜɵɪɚɠɟɧɢɟ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɤ ɮɨɪɦɭɥɟ Ʉɥɨɫɫɚ, ɪɚɡ-

ɞɟɥɢɜ (3.83) ɧɚ (3.85).

		2 MɄɌ
M					.
		Įs		ĮsɄɌ		(3.86)
		ĮsɄɌ		Įs

ɉɨɥɭɱɟɧɧɨɟ ɜɵɪɚɠɟɧɢɟ ɧɚɩɨɦɢɧɚɟɬ ɭɩɪɨɳɟɧɧɭɸ ɮɨɪɦɭɥɭ Ʉɥɨɫɫɚ ɫ ɬɨɣ ɥɢɲɶ ɪɚɡɧɢɰɟɣ, ɱɬɨ ɧɟ ɛɵɥɨ ɫɞɟɥɚɧɨ ɧɢɤɚɤɢɯ ɞɨɩɭɳɟɧɢɣ (ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɢɫɬɨɱɧɢɤɚ ɧɚɩɪɹɠɟɧɢɹ ɩɪɢɧɢɦɚɥɢ r1 = 0). ɉɨ (3.86) ɫ ɭɱɟɬɨɦ (3.84) ɢ (3.85) ɫɬɪɨɢɬɫɹ ɦɟɯɚɧɢɱɟɫɤɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɢɫɬɨɱɧɢɤɚ ɬɨɤɚ.

ɋɤɨɪɨɫɬɶ ɞɜɢɝɚɬɟɥɹ Ȧ ɭɱɢɬɵɜɚɟɬɫɹ ɚɛɫɨɥɸɬɧɵɦ ɫɤɨɥɶɠɟɧɢɟɦ

	Į Ȧ0ɇ				Ȧ
Įs						, ɨɬɤɭɞɚ
	Ȧ0ɇ
Ȧ	Ȧ0		Įs Ȧ0ɇ Į Ȧ0ɇ 1					s Ȧ0ɇ Į		Įs .

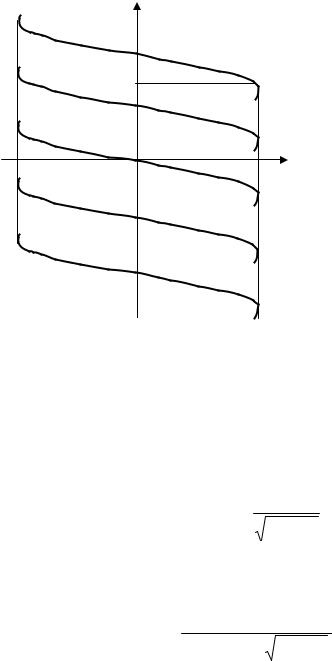
ɇɚ ɪɢɫ. 3.64 ɩɨɫɬɪɨɟɧɚ ɦɟɯɚɧɢɱɟɫɤɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɢɫɬɨɱɧɢɤɚ ɬɨɤɚ, ɩɪɨɯɨɞɹɳɚɹ ɱɟɪɟɡ ɬɨɱɤɢ Ȧ = Ȧ0ɇ, Ɇ = 0 ɢ Ȧ = ȦɄɌ, Ɇ = ɆɄɌ.

131

				Ɉɛɪɚɬɢɬɟ		ɜɧɢɦɚɧɢɟ, ɱɬɨ ɩɪɢ ɚɛɫɨ-
	Ȧ			ɥɸɬɧɨɦ ɫɤɨɥɶɠɟɧɢɢ Įs ɜ ɜɵɪɚɠɟɧɢɹɯ
	Ȧ0ɇ	f1ɇ		ɞɥɹ ɆɄɌ ɢ ĮsɄɌ ɢɧɞɭɤɬɢɜɧɵɟ ɫɨɩɪɨɬɢɜɥɟ-
				ɧɢɹ ɯc2 ɢ ɯμ ɫɬɚɧɨɜɹɬɫɹ ɩɨɫɬɨɹɧɧɵɦɢ, ɧɟ
				ɡɚɜɢɫɹɬ	ɨɬ	ɱɚɫɬɨɬɵ (ɨɧɢ	ɨɩɪɟɞɟɥɟɧɵ
	ȦɄɌ	f1<f1ɇ		ɩɪɢ ɧɨɦɢɧɚɥɶɧɨɣ ɱɚɫɬɨɬɟ f1ɇ ɢ ɧɨɦɢ-
				ɧɚɥɶɧɨɦ ɧɚɩɪɹɠɟɧɢɢ U1ɇ). Ʉɪɢɬɢɱɟɫɤɢɣ
		ɆɄɌ		ɦɨɦɟɧɬ ɬɚɤɠɟ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɱɚɫɬɨɬɵ Ɇ
							ɄɌ
			Ɇ	= const.	ȼ ɮɨɪɦɭɥɚɯ ɨɬɫɭɬɫɬɜɭɟɬ ɚɤɬɢɜ-
- ɆɄɌ		f1=0		ɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɫɬɚɬɨɪɚ r1.
				Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɢɫ-
	- Ȧ0
				ɬɨɱɧɢɤɚ ɬɨɤɚ ɡɚɜɢɫɢɬ ɨɬ ɱɚɫɬɨɬɵ ɬɨɥɶɤɨ
				ɫɢɧɯɪɨɧɧɚɹ ɫɤɨɪɨɫɬɶ Ȧ0, ɚ ɤɪɢɬɢɱɟɫɤɢɣ
	- Ȧ0ɇ			ɦɨɦɟɧɬ	ɢ	ɚɛɫɨɥɸɬɧɨɟ	ɤɪɢɬɢɱɟɫɤɨɟ
				ɫɤɨɥɶɠɟɧɢɟ ɨɫɬɚɸɬɫɹ ɩɨɫɬɨɹɧɧɵɦɢ. ȼ
				ɷɬɢɯ ɭɫɥɨɜɢɹɯ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɱɚɫɬɨɬɵ
Ɋɢɫ. 3.64. Ɇɟɯɚɧɢɱɟɫɤɢɟ				(f1 = var) ɬɨɤɚ ɫɬɚɬɨɪɚ ɦɟɯɚɧɢɱɟɫɤɢɟ ɯɚ-
				ɪɚɤɬɟɪɢɫɬɢɤɢ ɩɪɨɯɨɞɹɬ			ɩɚɪɚɥɥɟɥɶɧɨ

	ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɞɜɢɝɚɬɟɥɹ	ɞɪɭɝ ɞɪɭɝɭ ɱɟɪɟɡ ɪɚɡɧɵɟ ɬɨɱɤɢ ɫɢɧɯɪɨɧ-
	ɜ ɫɢɫɬɟɦɟ ɂɌ – ȺȾ
		ɧɨɣ ɫɤɨɪɨɫɬɢ (ɫɦ. ɪɢɫ. 3.64).
		ɋɪɚɜɧɟɧɢɟ ɦɟɯɚɧɢɱɟɫɤɢɯ ɯɚɪɚɤɬɟɪɢ-

ɫɬɢɤ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɢɫɬɨɱɧɢɤɚ ɧɚɩɪɹɠɟɧɢɹ ɂɇ ɢ ɨɬ ɢɫɬɨɱɧɢɤɚ ɬɨɤɚ ɂɌ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 3.65.

ɉɪɢ ɧɨɦɢɧɚɥɶɧɨɣ ɱɚɫɬɨɬɟ (Į = 1) ɤɪɢɬɢɱɟɫɤɨɟ ɫɤɨɥɶɠɟɧɢɟ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɇ sɄ > ĮsɄɌ,

s	r	r2c	> Įs	r		r2c	,
					xc2
K	r2 x2		ɄɌ			xμ
	1	K

ɬɚɤ ɤɚɤ ɯɄ << ɯμ.

Ʉɪɢɬɢɱɟɫɤɢɣ ɦɨɦɟɧɬ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɌ ɆɄɌ < ɆɄ ɢɡ-ɡɚ ɯμ, ɧɚɯɨɞɹɳɟɝɨɫɹ ɜ ɡɧɚɦɟɧɚɬɟɥɟ

	3 U2	3 I12 xμ2
MK	2 Ȧ0 r1 r 1 r12 xɄ2 ! MɄɌ		.
		2 Ȧ0ɇ (xc2 xμ )

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɟɯɚɧɢɱɟɫɤɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɌ ɨɛɥɚɞɚɟɬ ɦɟɧɶɲɢɦ ɤɪɢɬɢɱɟɫɤɢɦ ɦɨɦɟɧɬɨɦ ɆɄɌ < ɆɄ, ɧɨ ɛɨɥɶɲɟɣ ɤɪɢɬɢɱɟɫɤɨɣ ɫɤɨɪɨɫɬɶɸ ȦɄɌ > ȦɄ, ɜɫɥɟɞɫɬɜɢɟ ɱɟɝɨ ɨɧɚ ɞɨɥɠɧɚ ɛɵɬɶ ɡɧɚɱɢɬɟɥɶɧɨ ɠɟɫɬɱɟ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɇ.

ɇɚ ɜɢɞ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɌ ɫɭɳɟɫɬɜɟɧɧɨɟ ɜɥɢɹɧɢɟ ɨɤɚɡɵɜɚɟɬ ɜɟɥɢɱɢɧɚ ɬɨɤɚ ɫɬɚɬɨɪɚ I1, ɬɚɤ ɤɚɤ ɤɪɢɬɢɱɟɫɤɢɣ ɦɨɦɟɧɬ ɆɄ ɩɪɨɩɨɪɰɢɨɧɚɥɟɧ ɤɜɚɞɪɚɬɭ ɬɨɤɚ I1, ɩɪɢ ɩɨɫɬɨɹɧɫɬɜɟ ĮsɄɌ. ɉɪɢ ɜɜɟɞɟɧɢɢ ɞɨɛɚɜɨɱɧɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜ ɰɟɩɶ ɪɨɬɨɪɚ R2ȾɈȻ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɟɦɭ ɢɡɦɟɧɹɟɬɫɹ ɤɪɢɬɢɱɟɫɤɨɟ ɫɤɨɥɶɠɟɧɢɟ ĮsɄɌ, ɢɡɦɟɧɹɹ ɠɟɫɬɤɨɫɬɶ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɩɪɢ ɧɟɢɡɦɟɧɧɨɣ ɜɟɥɢɱɢɧɟ ɤɪɢɬɢɱɟɫɤɨɝɨ ɦɨɦɟɧɬɚ ɆɄɌ.

Ɋɚɫɫɦɨɬɪɟɧɧɵɟ ɜɵɲɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɧɟ ɭɱɢɬɵɜɚɥɢ ɢɡɦɟɧɟɧɢɟ ɯμ, ɩɪɢɧɢɦɚ-

ɥɨɫɶ ɯμ = const.

132

		Ɉɬɧɨɫɢɬɟɥɶɧɨ ɦɚɥɨɟ ɡɧɚɱɟɧɢɟ ɤɪɢɬɢɱɟ-
Ȧ
Ȧ0		ɫɤɨɝɨ ɦɨɦɟɧɬɚ ɆɄɌ ɩɨɛɭɠɞɚɟɬ ɭɜɟɥɢɱɢɜɚɬɶ
ɂɇ		ɬɨɤ ɫɬɚɬɨɪɚ ɞɨ 2…4ǜI1ɇ, ɱɬɨ ɜ ɫɜɨɸ ɨɱɟɪɟɞɶ
ȦɄɌ		ɩɪɢɜɨɞɢɬ ɤ ɧɚɫɵɳɟɧɢɸ ɞɜɢɝɚɬɟɥɹ ɢ ɧɟɨɛ-
		ɯɨɞɢɦɨɫɬɢ ɭɱɟɬɚ ɢɡɦɟɧɟɧɢɹ ɢɧɞɭɤɬɢɜɧɨɝɨ
ȦɄ
		ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɤɨɧɬɭɪɚ ɧɚɦɚɝɧɢɱɢɜɚɧɢɹ ɯμ
		= var.
ɂɌ
		ɍɜɟɥɢɱɟɧɢɟ I1 ɩɪɢɜɨɞɢɬ ɤ ɭɦɟɧɶɲɟɧɢɸ
		ɯμ, ɢ ɤɪɢɬɢɱɟɫɤɢɣ ɦɨɦɟɧɬ ɞɜɢɝɚɬɟɥɹ ɜɨɡ-
	Ɇ	ɪɚɫɬɟɬ ɜ ɦɟɧɶɲɟɣ ɫɬɟɩɟɧɢ, ɱɟɦ ɨɠɢɞɚɜ-
ɆɄɌ		ɲɟɟɫɹ ɟɝɨ ɭɜɟɥɢɱɟɧɢɟ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ
	ɆɄ	ɤɜɚɞɪɚɬɭ ɬɨɤɚ. ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɭɦɟɧɶ-
Ɋɢɫ. 3.65. ɋɪɚɜɧɟɧɢɟ		ɲɟɧɢɟ ɯμ ɭɜɟɥɢɱɢɜɚɟɬ ɤɪɢɬɢɱɟɫɤɨɟ ɫɤɨɥɶ-
ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɞɜɢɝɚɬɟɥɹ		ɠɟɧɢɟ ĮsɄɌ, ɱɬɨ ɭɜɟɥɢɱɢɜɚɟɬ ɧɚɤɥɨɧ ɯɚɪɚɤ-
ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɌ ɢ ɂɇ		ɬɟɪɢɫɬɢɤɢ.
		Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɭɱɟɬ ɯμ ɩɪɢɜɨɞɢɬ ɤ
		ɩɪɚɤɬɢɱɟɫɤɨɦɭ ɜɢɞɭ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤ-
		ɬɟɪɢɫɬɢɤɢ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɟɝɨ ɨɬ ɂɌ. ȼ ɷɬɢɯ

ɭɫɥɨɜɢɹɯ ɪɚɫɱɟɬ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɜɵɩɨɥɧɹɟɬɫɹ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ Ɍ–ɨɛɪɚɡɧɨɣ ɫɯɟɦɵ ɡɚɦɟɳɟɧɢɹ ɫ ɭɱɟɬɨɦ ɢɡɦɟɧɟɧɢɹ ɯμ ɩɨ ɭɪɚɜɧɟɧɢɹɦ (3.70) ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɩɪɨɝɪɚɦɦɵ «harad».

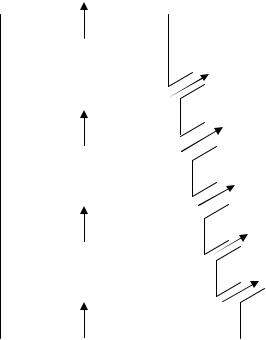
ɗɥɟɤɬɪɨɦɟɯɚɧɢɱɟɫɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɂɌ – ȺȾ. ɂɡ ɜɟɤɬɨɪɧɨɣ ɞɢɚɝɪɚɦɦɵ

(ɪɢɫ. 3.63) ɜɢɞɟɧ ɯɚɪɚɤɬɟɪ ɢɡɦɟɧɟɧɢɹ ɬɨɤɨɜ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɫɤɨɪɨɫɬɢ ɢ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɫɤɨɥɶɠɟɧɢɹ ɞɜɢɝɚɬɟɥɹ.

ɉɪɢ s = 0 ɬɨɤ ɫɬɚɬɨɪɚ ɪɚɜɟɧ ɬɨɤɭ ɧɚɦɚɝɧɢɱɢɜɚɧɢɹ I1 = Iμ, ɚ ɬɨɤ ɪɨɬɨɪɚ ɪɚɜɟɧ ɧɭɥɸ Ic2= 0.

ɉɪɢ ɪɨɫɬɟ ɦɨɦɟɧɬɚ ɧɚ ɜɚɥɭ ɪɚɫɬɭɬ ɫɤɨɥɶɠɟɧɢɟ s, ɗȾɋ ɢ ɬɨɤ ɪɨɬɨɪɚ Ic2.

Ɍɨɤ ɫɬɚɬɨɪɚ I1 = const ɢ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɬɨɤɚ ɪɨɬɨɪɚ ɢɡɦɟɧɹɟɬɫɹ ɩɨ ɮɚɡɟ ɩɨ ɞɭɝɟ ɨɤɪɭɠɧɨɫɬɢ. ɋ ɪɨɫɬɨɦ ɬɨɤɚ ɪɨɬɨɪɚ ɭɦɟɧɶɲɚɟɬɫɹ ɬɨɤ ɧɚɦɚɝɧɢɱɢɜɚɧɢɹ.

ɉɨ ɡɚɤɨɧɭ ɪɚɡɞɟɥɟɧɢɹ ɬɨɤɨɜ ɜ ɩɚɪɚɥɥɟɥɶɧɵɯ ɰɟɩɹɯ ɧɚɣɞɟɦ ɬɨɤ ɪɨɬɨɪɚ

Ic2	I1 xμ
	r2c /Ds 2 xc2 xμ 2	(3.87)

ɢ ɬɨɤ ɧɚɦɚɝɧɢɱɢɜɚɧɢɹ

I	I	r2c	/Ds 2 xc22		.
				2		(3.88)
μ	1	r2c /Ds 2 xc2 xμ

ɉɪɢ s f ɬɨɤɢ ɫɬɪɟɦɹɬɫɹ ɤ ɩɪɟɞɟɥɶɧɵɦ ɡɧɚɱɟɧɢɹɦ:

Ic

xμ

xc

I

# I ;

I

I

2

# 0.

x

xc

x

2

ɉɊȿȾ

1

μ

1

PɉɊȿȾ

1

μ

xc

2

2

133

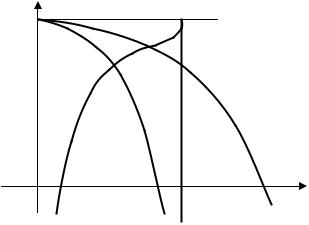
Ɋɚɫɫɦɨɬɪɟɧɧɵɟ ɡɚɜɢɫɢɦɨɫɬɢ ɩɪɢɜɟɞɟɧɵ ɧɚ ɪɢɫ. 3.66. ɋɬɪɟɦɥɟɧɢɟ ɤ ɧɭɥɸ Iμ ɨɡɧɚɱɚɟɬ ɬɚɤɠɟ, ɱɬɨ ɤ ɧɭɥɸ ɫɬɪɟɦɢɬɫɹ ɢ ɩɨɬɨɤ ɦɚɲɢɧɵ, ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɢ ɪɚɡɜɢɜɚɟɦɵɣ ɟɸ ɦɨɦɟɧɬ. ɗɬɨ ɞɨɤɚɡɵɜɚɟɬ ɧɟɨɛɯɨɞɢɦɨɫɬɶ ɪɚɫɱɟɬɚ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɩɪɢ ɯμ = var. ɇɟɨɛɯɨɞɢɦɨ ɨɬɦɟɬɢɬɶ ɬɚɤɠɟ ɜɵɫɨɤɭɸ ɠɟɫɬɤɨɫɬɶ ɪɚɛɨɱɟɝɨ ɭɱɚɫɬɤɚ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ, ɤɨɬɨɪɚɹ ɧɟ ɩɨɡɜɨɥɹɟɬ ɞɜɢɝɚɬɟɥɸ ɭɫɬɨɣɱɢɜɨ ɪɚɛɨɬɚɬɶ ɩɪɢ ɤɨɥɟɛɚɧɢɹɯ ɦɨɦɟɧɬɚ ɧɚ ɜɚɥɭ ɢ ɫɤɨɪɨɫɬɢ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɩɪɢ ɩɢɬɚɧɢɢ ȺȾ ɨɬ ɂɌ ɩɪɢɯɨɞɢɬɫɹ ɩɪɢɦɟɧɹɬɶ ɨɬɪɢɰɚɬɟɥɶɧɭɸ ɨɛɪɚɬɧɭɸ ɫɜɹɡɶ ɩɨ ɫɤɨɪɨɫɬɢ.

ȦȦ0ɇ

I1

Iμ

I2|	Ec2 I, Ec2

Ɋɢɫ. 3.66. ɗɥɟɤɬɪɨɦɟɯɚɧɢɱɟɫɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ȺȾ ɩɪɢ ɩɢɬɚɧɢɢ ɨɬ ɂɌ

3.5.9. ɉɭɫɤ ȺȾ

ɋɩɨɫɨɛɵ ɩɭɫɤɚ ɚɫɢɧɯɪɨɧɧɨɝɨ ɞɜɢɝɚɬɟɥɹ ɫ ɤɨɪɨɬɤɨɡɚɦɤɧɭɬɵɦ ɪɨɬɨɪɨɦ:

– ɩɪɹɦɨɣ ɩɭɫɤ – ɩɪɢ ɩɢɬɚɧɢɢ ɞɜɢɝɚɬɟɥɹ ɨɬ ɫɟɬɢ ɧɟɢɡɦɟɧɧɨɝɨ ɧɚɩɪɹɠɟɧɢɹ, ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɫɬɚɬɨɪ ɩɨɞɚɟɬɫɹ ɫɤɚɱɤɨɦ. ɉɭɫɤ ɩɪɨɢɡɜɨɞɢɬɫɹ ɧɚ ɟɫɬɟɫɬɜɟɧɧɨɣ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ (ɫɦ. ɩ. 3.5.7). ɉɪɢ ɩɭɫɤɨɜɨɦ (s = 1) ɦɨɦɟɧɬɟ Ɇɉ = 0,8…1,8 Ɇɇ ɩɭɫɤɨɜɨɣ ɬɨɤ ɫɬɚɬɨɪɚ I1ɉ ɞɨɫɬɢɝɚɟɬ ɡɧɚɱɟɧɢɹ 5…7·I 1ɇ. ɉɚɞɟɧɢɟ ɧɚɩɪɹɠɟɧɢɹ ɜ ɫɟɬɢ, ɩɢɬɚɸɳɟɣ ɞɜɢɝɚɬɟɥɶ, ɩɪɢ ɩɭɫɤɟ ɦɨɠɟɬ ɩɪɟɜɵɫɢɬɶ ɞɨɩɭɫɤɚɟɦɨɟ ɩɨ ɭɫɥɨɜɢɹɦ ɷɤɫɩɥɭɚɬɚɰɢɢ –10% Uɇ.

– ɪɟɚɤɬɨɪɧɵɣ (ɪɟɠɟ ɚɜɬɨɬɪɚɧɫɮɨɪɦɚɬɨɪɧɵɣ) – ɜ ɰɟɩɶ ɫɬɚɬɨɪɚ ɧɚ ɜɪɟɦɹ ɩɭɫɤɚ ɜɤɥɸɱɚɸɬ ɥɢɛɨ ɪɟɚɤɬɨɪɵ, ɥɢɛɨ ɚɜɬɨɬɪɚɧɫɮɨɪɦɚɬɨɪ ɫ ɰɟɥɶɸ ɨɝɪɚɧɢɱɟɧɢɹ ɩɭɫɤɨɜɨɝɨ ɬɨɤɚ ɢ ɞɨɫɬɢɠɟɧɢɹ ɩɚɞɟɧɢɟɦ ɧɚɩɪɹɠɟɧɢɹ ɜ ɫɟɬɢ ɞɨɩɭɫɤɚɟɦɨɝɨ ɡɧɚɱɟɧɢɹ. ɉɪɢ ɩɭɫɤɟ ɚɫɢɧɯɪɨɧɧɨɝɨ ɞɜɢɝɚɬɟɥɹ ɫ ɮɚɡɧɵɦ ɪɨɬɨɪɨɦ ɫ ɰɟɥɶɸ ɨɛɟɫɩɟɱɟɧɢɹ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɯ ɬɪɟɛɨɜɚɧɢɣ, ɩɪɟɞɴɹɜɥɹɟɦɵɯ ɤ ɩɭɫɤɭ (ɮɨɪɫɢɪɨɜɚɧɧɵɣ, ɫ ɨɝɪɚɧɢɱɟɧɢɟɦ ɩɨ ɭɫɤɨɪɟɧɢɸ ɪɚɛɨɱɟɝɨ ɨɪɝɚɧɚ, ɧɨɪɦɚɥɶɧɵɣ ɩɭɫɤ – ɫɦ. ɩ. 3.1.6) ɜ ɰɟɩɶ ɪɨɬɨɪɚ ɜɤɥɸɱɚɸɬ ɞɨɛɚɜɨɱɧɵɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ R2ȾɈȻ. ɍɜɟɥɢɱɟɧɢɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɪɨɬɨɪɚ ɩɪɢɜɨɞɢɬ ɤ ɫɧɢɠɟɧɢɸ ɬɨɤɚ ɪɨɬɨɪɚ I2 ɩɪɢ ɨɞɧɨɜɪɟɦɟɧɧɨɦ ɪɨɫɬɟ ɟɝɨ ɚɤɬɢɜɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ I2Ⱥ ɢ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɤ ɭɜɟɥɢɱɟɧɢɸ ɩɭɫɤɨɜɨɝɨ ɦɨɦɟɧɬɚ Ɇɉ.

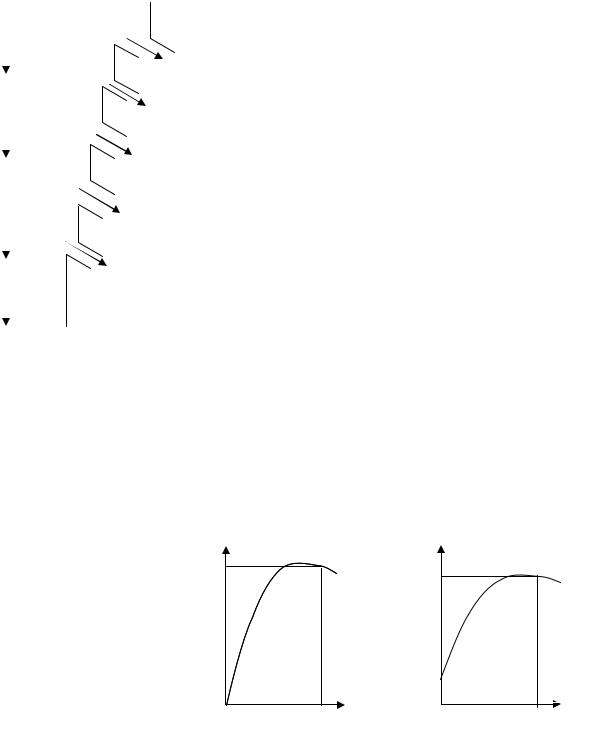
Ɋɟɨɫɬɚɬɧɵɣ ɩɭɫɤ ȺȾɎɊ. ɇɚ ɪɢɫ. 3.67 ɩɪɢɜɟɞɟɧɚ ɫɯɟɦɚ ɫɢɥɨɜɵɯ ɰɟɩɟɣ ɪɟɨɫɬɚɬɧɨɝɨ ɩɭɫɤɚ ɞɜɢɝɚɬɟɥɹ. Ɋɟɨɫɬɚɬɧɵɣ ɩɭɫɤ ɩɪɟɞɭɫɦɚɬɪɢɜɚɟɬ ɩɪɢ ɩɨɞɚɱɟ ɧɚɩɪɹɠɟɧɢɹ ɧɚ ɫɬɚɬɨɪ ɜɜɟɞɟɧɢɟ ɞɨɛɚɜɨɱɧɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ, ɨɝɪɚɧɢɱɢɜɚɸɳɟɝɨ ɜɟɥɢɱɢɧɭ ɬɨɤɚ ɪɨɬɨɪɚ ɞɨɩɭɫɬɢɦɵɦ ɡɧɚɱɟɧɢɟɦ ɩɨ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɦ ɭɫɥɨɜɢɹɦ ɩɭɫɤɚ. ɇɚ ɪɢɫ. 3.68 ɩɪɢɜɟɞɟɧɵ ɦɟɯɚɧɢɱɟɫɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ, ɨɛɟɫɩɟɱɢɜɚɸɳɢɟ ɩɭɫɤ ɞɜɢɝɚɬɟɥɹ. ɉɪɢ ɡɚɦɵɤɚɧɢɢ ɤɨɧɬɚɤɬɨɜ ɥɢɧɟɣɧɨɝɨ ɤɨɧɬɚɤɬɨɪɚ ɄɅ ɢ ɨɞɧɨɝɨ ɢɡ ɤɨɧɬɚɤɬɨɪɨɜ ɧɚɩɪɚɜɥɟɧɢɹ Ʉȼ (ɢɥɢ Ʉɇ) ɬɨɤ ɪɨɬɨɪɚ I2 ɩɪɨɬɟɤɚɟɬ ɱɟɪɟɡ ɨɛɦɨɬɤɭ ɪɨɬɨɪɚ ɢ ɞɨɛɚɜɨɱɧɵɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ R1ȾɈȻ ɢ R2ȾɈȻ, ɫɨɡɞɚɟɬɫɹ ɦɨɦɟɧɬ Ɇ1. Ʉɨɧɬɚɤɬɨɪ ɪɟɠɢɦɚ ɩɪɨɬɢɜɨɜɤɥɸɱɟɧɢɹ Ʉɉȼ ɜɨ ɜɪɟɦɹ ɩɭɫɤɚ ɜɤɥɸɱɟɧ, ɢ ɫɨɩɪɨɬɢɜɥɟɧɢɟ Rɉȼ ȾɈȻ ɡɚɲɭɧɬɢɪɨɜɚɧɨ. Ⱦɜɢɝɚɬɟɥɶ ɪɚɡɝɨɧɹɟɬɫɹ ɩɨ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ ɫ R1ȾɈȻ + R2ȾɈȻ , ɬɨɤ ɪɨɬɨɪɚ ɫɧɢɠɚɟɬɫɹ, ɢ ɦɨɦɟɧɬɟ ɩɟɪɟɤɥɸɱɟɧɢɹ Ɇ2 ɜɤɥɸɱɚɟɬɫɹ ɤɨɧɬɚɤɬɨɪ Ʉɍ1, ɲɭɧɬɢɪɭɹ R1ȾɈȻ. Ⱦɜɢɝɚɬɟɥɶ ɩɟɪɟɜɨɞɢɬɫɹ ɧɚ ɯɚɪɚɤɬɟɪɢɫɬɢɤɭ ɫ R2ȾɈȻ. Ɍɨɤ

134

ɪɨɬɨɪɚ ɜɧɨɜɶ ɭɜɟɥɢɱɢɜɚɟɬɫɹ, ɦɨɦɟɧɬ ɧɚɪɚɫɬɚɟɬ ɞɨ ɡɧɚɱɟɧɢɹ Ɇ1. ɉɪɨɢɫɯɨɞɢɬ ɪɚɡɝɨɧ ɞɨ ɫɤɨɪɨɫɬɢ, ɝɞɟ ɩɪɢ ɦɨɦɟɧɬɟ ɩɟɪɟɤɥɸɱɟɧɢɹ Ɇ2 ɜɤɥɸɱɚɟɬɫɹ ɤɨɧɬɚɤɬɨɪ Ʉɍ2, ɩɟɪɟɜɨɞɹ ɞɜɢɝɚɬɟɥɶ ɧɚ ɟɫɬɟɫɬɜɟɧɧɭɸ ɯɚɪɚɤɬɟɪɢɫɬɢɤɭ. ɇɚ ɷɬɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ ɩɪɨɞɨɥɠɚɟɬɫɹ ɪɚɡɝɨɧ ɞɨ ɫɤɨɪɨɫɬɢ Ȧɋ, ɝɞɟ ɩɪɢ Ɇ = Ɇɋ ɞɜɢɝɚɬɟɥɶ ɩɟɪɟɯɨɞɢɬ ɜ ɭɫɬɚɧɨɜɢɜɲɢɣɫɹ ɪɟɠɢɦ ɪɚɛɨɬɵ (ɬɨɱɤɚ 1). ȼ ɩɪɨɰɟɫɫɟ ɪɚɡɝɨɧɚ ɞɜɢɝɚɬɟɥɹ ɞɨɛɚɜɨɱɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɭɦɟɧɶɲɚɸɬ ɩɨ ɜɟɥɢɱɢɧɟ, ɨɛɟɫɩɟɱɢɜɚɹ ɩɟɪɟɤɥɸɱɟɧɢɟ ɫɬɭɩɟɧɟɣ ɩɭɫɤɨɜɵɯ ɫɨɩɪɨɬɢɜɥɟɧɢɣ ɩɨ ɩɪɚɜɢɥɶɧɨɣ ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɟ. ɉɟɪɟɤɥɸɱɟɧɢɟ ɫɬɭɩɟɧɟɣ ɜɵɩɨɥɧɹɟɬɫɹ ɚɜɬɨɦɚɬɢɱɟɫɤɢ ɜ ɮɭɧɤɰɢɢ ɜɪɟɦɟɧɢ, ɬɨɤɚ, ɫɤɨɪɨɫɬɢ.

~

Ʉȼ.

Ʉɇ

ɄɅ

Ɇ

Ʉɍ2

R2ȾɈȻ

Ʉɍ1

R1ȾɈȻ

Ʉɉȼ

RɉȼȾɈȻ

ɉɪɚɜɢɥɶɧɚɹ ɩɭɫɤɨɜɚɹ ɞɢɚɝɪɚɦɦɚ ɫɬɪɨɢɬɫɹ ɢɡ ɭɫɥɨɜɢɹ ɩɨɞɞɟɪɠɚɧɢɹ ɩɨɫɬɨɹɧɫɬɜɚ ɫɪɟɞɧɟɝɨ ɩɭɫɤɨɜɨɝɨ ɦɨɦɟɧɬɚ ɞɜɢɝɚɬɟɥɹ, ɨɛɟɫɩɟɱɢɜɚɹ ɪɚɜɟɧɫɬɜɨ ɦɚɤɫɢɦɚɥɶɧɵɯ ɦɨɦɟɧɬɨɜ Ɇ1 ɧɚ ɤɚɠɞɨɣ ɢɡ ɩɭɫɤɨɜɵɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ, ɚ ɬɚɤɠɟ ɪɚɜɟɧɫɬɜɨ ɦɨɦɟɧɬɨɜ ɩɟɪɟɤɥɸɱɟɧɢɹ Ɇ2 (ɪɢɫ. 3.68).

ɉɭɫɤɨɜɵɟ ɪɟɡɢɫɬɨɪɵ ɪɚɫɫɱɢɬɵɜɚɸɬɫɹ ɚɧɚɥɨɝɢɱɧɨ ɪɚɫɫɦɨɬɪɟɧɧɨɦɭ ɜɵɲɟ ɪɚɫɱɟɬɭ ɞɥɹ Ⱦɇȼ (ɫɦ. ɩ. 3.1.6):

–ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨɥɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɰɟɩɢ ɪɨɬɨɪɚ ɩɪɢ ɩɭɫɤɟ R2;

–ɜɵɩɨɥɧɹɟɬɫɹ ɪɚɡɛɢɟɧɢɟ R2 ɧɚ ɫɬɭɩɟɧɢ, ɨɛɟɫɩɟɱɢɜɚɸɳɢɟ ɩɪɚɜɢɥɶɧɭɸ ɩɭɫɤɨɜɭɸ ɞɢɚɝɪɚɦɦɭ.

		Ȧ
		Ȧ0ɇ	1
3
				ɟɫɬ
	ɉȼ			R2ȾɈȻ
		ɆɄɁ
				Ɇ
4		ɆC	Ɇ2	Ɇ1
			R1ȾɈȻ	R1ȾɈȻ+
		ɉȼ	+R2ȾɈȻ	+R2ȾɈȻ
			+RɉȼȾɈȻ
	- Ȧ0ɇ	2

Ɋɢɫ. 3.67. ɋɯɟɦɚ ɩɭɫɤɚ	Ɋɢɫ. 3.68. Ɇɟɯɚɧɢɱɟɫɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ȺȾ
	ɜ ɪɟɠɢɦɟ ɩɭɫɤɚ ɢ ɬɨɪɦɨɠɟɧɢɹ
ɢ ɪɟɜɟɪɫɚ ɫ ɬɨɪɦɨɠɟɧɢɟɦ
ɩɪɨɬɢɜɨɜɤɥɸɱɟɧɢɟɦ	ɩɪɨɬɢɜɨɜɤɥɸɱɟɧɢɟɦ

ɋ ɭɱɟɬɨɦ ɩɚɞɟɧɢɹ ɧɚɩɪɹɠɟɧɢɹ ɜ ɫɟɬɢ ɩɪɢ ɩɭɫɤɟ (ǻU1 = 0,1ǜU1ɇ) ɩɪɢɧɢɦɚɸɬ ɦɚɤɫɢɦɚɥɶɧɵɣ ɩɭɫɤɨɜɨɣ ɦɨɦɟɧɬ Ɇ1 d ɆɆȺɄɋ = 0,8ǜɆɄ. Ɇɨɦɟɧɬ ɩɟɪɟɤɥɸɱɟɧɢɹ ɜɵɛɢɪɚɸɬ Ɇ2 t 1,2ǜMC ɞɥɹ ɢɫɤɥɸɱɟɧɢɹ ɡɚɫɬɪɟɜɚɧɢɹ ɧɚ ɩɪɨɦɟɠɭɬɨɱɧɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ.

135

ȼ ɫɜɹɡɢ ɫ ɧɟɥɢɧɟɣɧɨɫɬɶɸ ɦɟɯɚɧɢɱɟɫɤɢɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɬɨɱɧɵɟ ɚɧɚɥɢɬɢɱɟɫɤɢɟ ɪɚɫɱɟɬɵ ɫɥɨɠɧɵ ɢ ɩɪɚɤɬɢɱɟɫɤɢ ɢɦɢ ɧɟ ɩɨɥɶɡɭɸɬɫɹ. ɉɪɢɦɟɧɹɸɬɫɹ ɩɪɢɛɥɢɠɟɧɧɵɟ ɫɩɨɫɨɛɵ, ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɧɟɨɛɯɨɞɢɦɨɣ ɬɨɱɧɨɫɬɢ, ɭɱɢɬɵɜɚɸɳɢɟ ɢɥɢ ɧɟ ɭɱɢɬɵɜɚɸɳɢɟ ɤɪɢɜɢɡɧɭ ɯɚɪɚɤɬɟɪɢɫɬɢɤ.

ɉɪɢɦɟɪ 3.9. Ɋɚɫɫɱɢɬɚɬɶ ɢ ɩɨɫɬɪɨɢɬɶ ɩɪɚɜɢɥɶɧɭɸ ɩɭɫɤɨɜɭɸ ɞɢɚɝɪɚɦɦɭ, ɨɛɟɫɩɟɱɢɜɚɸɳɭɸ ɩɭɫɤ ɚɫɢɧɯɪɨɧɧɨɝɨ ɞɜɢɝɚɬɟɥɹ (ɤɚɬɚɥɨɠɧɵɟ ɞɚɧɧɵɟ ɫɦ. ɜ ɩɪɢɦɟɪɟ 3.5) ɩɪɢ Ɇɋ = 0,5 ɡɚ ɦɢɧɢɦɚɥɶɧɨɟ ɜɪɟɦɹ. ɉɪɢɧɹɬɶ ɱɢɫɥɨ ɫɬɭɩɟɧɟɣ m = 3.

Ⱦɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɦɢɧɢɦɚɥɶɧɨɝɨ ɜɪɟɦɟɧɢ ɩɭɫɤɚ ɞɜɢɝɚɬɟɥɶ ɞɨɥɠɟɧ ɪɚɛɨɬɚɬɶ ɫ

ɩɪɟɞɟɥɶɧɵɦ ɦɨɦɟɧɬɨɦ ɆȾɈɉ = 0,8ǜɆɄ = 0,8·3·198 = 475 ɇɦ.

3.9.1. ɉɪɢ ɪɚɫɱɟɬɟ ɛɟɡ ɭɱɟɬɚ ɤɪɢɜɢɡɧɵ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɩɪɢɧɢɦɚɸɬ ɡɚ ɟɫɬɟɫɬɜɟɧɧɭɸ ɯɚɪɚɤɬɟɪɢɫɬɢɤɭ ɟɟ ɩɪɹɦɨɥɢɧɟɣɧɵɣ ɭɱɚɫɬɨɤ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɯɚɪɚɤɬɟɪɢɫɬɢ-

ɤɚ ɩɪɨɯɨɞɢɬ ɱɟɪɟɡ ɬɨɱɤɢ (Ȧ = Ȧ0ɇ, Ɇ = 0) ɢ (Ȧ = Ȧɇ, Ɇ = Ɇɇ).

Ɋɚɫɱɟɬ ɦɨɠɧɨ ɜɵɩɨɥɧɢɬɶ ɩɨ ɦɟɬɨɞɢɤɟ ɪɚɫɱɟɬɚ ɩɪɚɜɢɥɶɧɨɣ ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɵ ɞɥɹ ɞɜɢɝɚɬɟɥɹ ɫ ɩɪɹɦɨɥɢɧɟɣɧɨɣ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɨɣ

(ɫɦ. ɩ. 3.1.5).

Ɇɚɤɫɢɦɚɥɶɧɵɣ ɦɨɦɟɧɬ ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɵ Ɇ1 = ɆȾɈɉ. Ɉɩɪɟɞɟɥɢɦ ɦɨɦɟɧɬ ɩɟɪɟɤɥɸɱɟɧɢɹ Ɇ2 ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɵ

Ɇ1 ɆȾɈɉ	2,4; Ȝ Ɇ1	m	1 3	1	2,28;
	Ɇ2		Ɇ1 sH	2,4 0,035

Ɇ2 Ɇ1/Ȝ 2,4/2,28 1,05.

Ɋɚɫɫɱɢɬɚɟɦ ɩɨɥɧɵɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜ ɰɟɩɢ ɪɨɬɨɪɚ ɧɚ ɤɚɠɞɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ:

R1

1/M1

1/2,4 0,417; R1

R1 R2H 0,417 7,42 3,094 Ɉɦ;

2 R2H

0,183 7,42 1,358 Ɉɦ;

R2

R1/Ȝ

0,417/2,28

0,183;

R2

R

3 R2H

0,08 7,42 0,534 Ɉɦ.

R3

R2/Ȝ

0,183/2,28

0,08;

R3

R

ɉɪɨɜɟɪɢɦ ɩɪɚɜɢɥɶɧɨɫɬɶ ɪɚɫɱɟɬɚ – ɧɚ ɩɨɫɥɟɞɧɟɣ ɫɬɭɩɟɧɢ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɞɨɥɠɧɨ ɛɵɬɶ ɪɚɜɧɨ ɧɟɜɵɤɥɸɱɚɟɦɨɦɭ.

R4 = R3/Ȝ = 0,08/2,28 = 0,035; R4 = r2c = sɇ;r2c = r2c 7,42 = 0,26 Ɉɦ.

ȼɟɥɢɱɢɧɵ ɫɬɭɩɟɧɟɣ ɫɨɩɪɨɬɢɜɥɟɧɢɣ:

R1ȾɈȻ = R1 – R2 = 3,094 – 1,358 = 1,736 Ɉɦ;

R2ȾɈȻ = R2 – R3 = 1,358 – 0,534 = 0,824 Ɉɦ; R3ȾɈȻ = R3 – rc2 = 0,534 – 0,26 = 0,274 Ɉɦ.

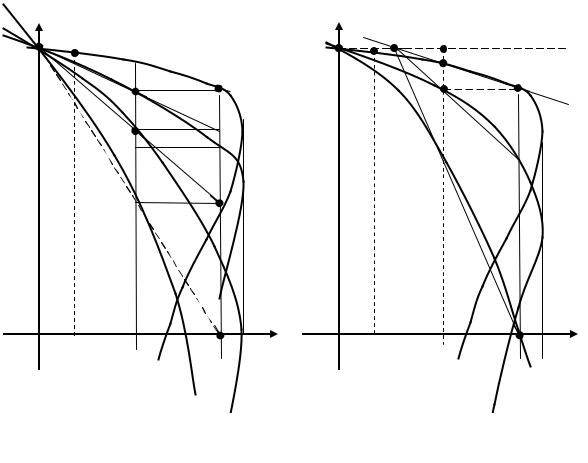
ɇɚ ɪɢɫ. 3.69,ɚ ɩɪɢɜɟɞɟɧɵ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɞɜɢɝɚɬɟɥɹ ɩɨ ɪɟɡɭɥɶɬɚɬɚɦ ɪɚɫɱɟɬɚ. Ɍɨɱɤɚɦɢ 1…7 ɨɬɦɟɱɟɧɵ ɪɚɫɱɟɬɧɵɟ ɡɧɚɱɟɧɢɹ ɫɤɨɪɨɫɬɟɣ ɢ ɦɨɦɟɧɬɨɜ. ȼɢɞɧɨ, ɱɬɨ ɦɚɤɫɢɦɚɥɶɧɵɟ ɦɨɦɟɧɬɵ (ɬɨɱɤɢ 1,3,5) ɧɟ ɩɨɩɚɥɢ ɧɚ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ, ɬɨɝɞɚ ɤɚɤ ɦɨɦɟɧɬɵ ɩɟɪɟɤɥɸɱɟɧɢɹ (ɬɨɱɤɢ 2,4,6) ɫɨɜɩɚɥɢ ɫ ɪɚɫɱɟɬɧɵɦɢ. Ɂɧɚɱɢɬ, ɩɪɢ ɪɚɫɱɟɬɟ ɩɪɚɜɢɥɶɧɨɣ ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɵ ɧɟɨɛɯɨɞɢɦ ɭɱɟɬ ɧɟɥɢɧɟɣɧɨɫɬɢ ɦɟɯɚɧɢɱɟɫɤɢɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ.

3.9.2. ɉɨɪɹɞɨɤ ɪɚɫɱɟɬɚ ɩɪɚɜɢɥɶɧɨɣ ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɵ ɫ ɭɱɟɬɨɦ ɤɪɢɜɢɡɧɵ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɦɟɬɨɞɨɦ ɥɭɱɟɜɨɣ ɞɢɚɝɪɚɦɦɵ:

–ɫɬɪɨɢɬɫɹ ɟɫɬɟɫɬɜɟɧɧɚɹ ɦɟɯɚɧɢɱɟɫɤɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ;

–ɚɧɚɥɨɝɢɱɧɨ ɡɚɞɚɱɟ 3.9.1 ɩɨ ɡɚɞɚɧɧɨɦɭ ɫɩɨɫɨɛɭ ɩɭɫɤɚ (ɮɨɪɫɢɪɨɜɚɧɧɵɣ, ɫ ɞɨɩɭɫɬɢɦɵɦ ɭɫɤɨɪɟɧɢɟɦ, ɧɨɪɦɚɥɶɧɵɣ) ɪɚɫɫɱɢɬɵɜɚɟɬɫɹ ɦɚɤɫɢɦɚɥɶɧɵɣ ɩɭɫɤɨɜɨɣ ɦɨɦɟɧɬ Ɇ1 (ɢɥɢ Ɇ2);

–ɧɚ ɟɫɬɟɫɬɜɟɧɧɨɣ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ (ɫɦ. ɪɢɫ. 3.69,ɛ) ɨɬɦɟɱɚɸɬ ɬɨɱɤɨɣ ”b” ɫɤɨɪɨɫɬɶ ɞɜɢɝɚɬɟɥɹ ɩɪɢ ɦɨɦɟɧɬɟ Ɇ1;

136

–ɡɚɞɚɸɬɫɹ ɦɨɦɟɧɬɨɦ ɩɟɪɟɤɥɸɱɟɧɢɹ Ɇ2 ɢ ɧɚ ɟɫɬɟɫɬɜɟɧɧɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ ɨɬɦɟɱɚɸɬ ɬɨɱɤɨɣ “a” ɫɤɨɪɨɫɬɶ ɞɜɢɝɚɬɟɥɹ ɩɪɢ ɦɨɦɟɧɬɟ Ɇ2;

–ɱɟɪɟɡ ɬɨɱɤɢ “a” ɢ ”b” ɩɪɨɜɨɞɹɬ ɩɪɹɦɭɸ ɞɨ ɩɟɪɟɫɟɱɟɧɢɹ ɫ ɝɨɪɢɡɨɧɬɚɥɶɸ, ɩɪɨɯɨɞɹɳɟɣ ɱɟɪɟɡ ɬɨɱɤɭ ɫɢɧɯɪɨɧɧɨɣ ɫɤɨɪɨɫɬɢ Ȧ0ɇ;

–ɬɨɱɤɚ ɩɟɪɟɫɟɱɟɧɢɹ “Ɉ” ɹɜɥɹɟɬɫɹ ɩɨɥɸɫɨɦ ɥɭɱɟɜɨɣ ɞɢɚɝɪɚɦɦɵ;

–ɫɨɟɞɢɧɹɸɬ ɬɨɱɤɭ “Ɉ” ɫ ɬɨɱɤɨɣ Ɇ1 ɩɪɢ ɫɤɨɪɨɫɬɢ Ȧ = 0;

–ɩɪɢ ɩɟɪɟɫɟɱɟɧɢɢ ɩɨɥɭɱɟɧɧɨɣ ɩɪɹɦɨɣ ɫ ɦɨɦɟɧɬɨɦ Ɇ2 ɜɵɩɨɥɧɹɸɬ ɩɟɪɟɯɨɞ ɩɪɢ ɩɨɫɬɨɹɧɫɬɜɟ ɫɤɨɪɨɫɬɢ ɤ ɦɨɦɟɧɬɭ Ɇ1;

–ɩɨɥɭɱɟɧɧɭɸ ɬɨɱɤɭ ɜɧɨɜɶ ɫɨɟɞɢɧɹɸɬ ɫ “Ɉ” ɢ ɬ.ɞ.

ɉɪɢ ɩɪɚɜɢɥɶɧɨ ɜɵɛɪɚɧɧɨɦ ɡɧɚɱɟɧɢɢ Ɇ2 ɜɵɯɨɞ ɧɚ ɟɫɬɟɫɬɜɟɧɧɭɸ ɯɚɪɚɤɬɟɪɢɫɬɢɤɭ ɩɨɥɭɱɚɸɬ ɩɪɢ ɦɨɦɟɧɬɟ Ɇ1 ɢ ɩɪɚɜɢɥɶɧɚɹ ɩɭɫɤɨɜɚɹ ɞɢɚɝɪɚɦɦɚ ɩɨɫɬɪɨɟɧɚ. ȿɫɥɢ ɩɪɚɜɢɥɶɧɚɹ ɩɭɫɤɨɜɚɹ ɞɢɚɝɪɚɦɦɚ ɧɟ ɩɨɥɭɱɟɧɚ, ɬɨ ɢɡɦɟɧɹɸɬ Ɇ2 ɢ ɩɨɜɬɨɪɹɸɬ ɩɨɫɬɪɨɟɧɢɟ ɞɨ ɟɟ ɩɨɥɭɱɟɧɢɹ.

ɉɪɢ ɩɨɫɬɨɹɧɫɬɜɟ ɦɨɦɟɧɬɚ ɫɤɨɥɶɠɟɧɢɟ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɫɨɩɪɨɬɢɜɥɟɧɢɸ ɜ ɰɟɩɢ ɪɨɬɨɪɚ, ɩɨɷɬɨɦɭ ɢɡɦɟɪɹɸɬ ɨɬɪɟɡɤɢ ɩɪɢ Ɇ = Ɇ2 (ɫɦ. ɪɢɫ. 3.69,ɛ) ɢ ɩɨ ɫɨɨɬɧɨɲɟɧɢɹɦ ɨɬɪɟɡɤɨɜ ɨɩɪɟɞɟɥɹɸɬ ɩɨɥɧɵɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɰɟɩɢ ɪɨɬɨɪɚ:

R1 = r2 ·(ce / ca); R2 = r2 (cd / ca),

ɝɞɟ r2 – ɧɟɜɵɤɥɸɱɚɟɦɨɟ ɚɤɬɢɜɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɮɚɡɵ ɪɨɬɨɪɚ.

Ɂɧɚɱɟɧɢɹ ɫɨɩɪɨɬɢɜɥɟɧɢɣ ɢɫɩɨɥɶɡɭɸɬ ɩɪɢ ɪɚɫɱɟɬɟ ɢɫɤɭɫɫɬɜɟɧɧɵɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɞɜɢɝɚɬɟɥɹ. Ʉɚɤ ɜɢɞɧɨ ɢɡ ɪɢɫ. 3.69, ɩɨɥɭɱɢɥɫɹ ɩɭɫɤ ɜ ɞɜɟ ɫɬɭɩɟɧɢ ɩɪɢ ɨɞɢɧɚɤɨɜɵɯ ɫ ɩɪɟɞɵɞɭɳɢɦ ɪɚɫɱɟɬɨɦ ɡɧɚɱɟɧɢɹɯ Ɇ1 ɢ Ɇ2. ɏɚɪɚɤɬɟɪɢɫɬɢɤɢ ɞɥɹ ɷɬɨɝɨ ɪɚɫɱɟɬɚ ɩɪɢɜɟɞɟɧɵ ɧɚ ɪɢɫ. 3.69,ɛ.

Ȧ		Ȧ	0
				ɫ	Ȧ0ɇ
				a
6	7			d	b

45

e

2 3

	M			M
	1
Mɋ M2	M1	Mɋ	M2	M1
ɚ)			ɛ)

Ɋɢɫ.3.69. ɉɨɫɬɪɨɟɧɢɟ ɩɪɚɜɢɥɶɧɨɣ ɩɭɫɤɨɜɨɣ ɞɢɚɝɪɚɦɦɵ ȺȾ ɚ) ɛɟɡ ɭɱɟɬɚ ɢ ɛ) ɫ ɭɱɟɬɨɦ ɤɪɢɜɢɡɧɵ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ

137

3.5.10. ɗɧɟɪɝɟɬɢɱɟɫɤɚɹ ɞɢɚɝɪɚɦɦɚ ȺȾ

ɗɧɟɪɝɟɬɢɱɟɫɤɚɹ ɞɢɚɝɪɚɦɦɚ ȺȾ ɫɬɪɨɢɬɫɹ ɞɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɩɨɬɟɪɶ ɦɨɳɧɨɫɬɢ ɜ ɩɪɨɰɟɫɫɟ ɷɥɟɤɬɪɨɦɟɯɚɧɢɱɟɫɤɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɷɧɟɪɝɢɢ, ɨɰɟɧɤɢ ɫɨɫɬɚɜɥɹɸɳɢɯ

ɩɨɬɟɪɶ ɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ – ɄɉȾ ɢ ɤɨɷɮɮɢɰɢɟɧɬɚ ɦɨɳɧɨɫɬɢ.
						Ɋɚɫɫɦɨɬɪɢɦ			ɷɧɟɪɝɟɬɢɱɟ-
	Ɋ1=3ǜU1ǜI1ǜcosij1					ɫɤɭɸ ɞɢɚɝɪɚɦɦɭ ɞɜɢɝɚɬɟɥɶɧɨ-
						ɝɨ ɪɟɠɢɦɚ ɪɚɛɨɬɵ ȺȾ (Ɇ > 0,
						Ȧ > 0), ɩɪɢɜɟɞɟɧɧɭɸ ɧɚ ɪɢɫ.
		ǻɊ	ǜ	2ǜ		3.70.
		1=3 I1		r1
	ɊɗɆ=ɆɗɆǜȦ0	ǻɊ ɉɈɋɌ=3ǜI			2ǜr	Ɇɨɳɧɨɫɬɶ		Ɋ1,	ɩɨɬɪɟɛɥɹɟ-
						ɦɚɹ ɢɡ ɫɟɬɢ		ɪɚɫɯɨɞɭɟɬɫɹ			ɧɚ
		1		1	μ		,
						ɫɨɡɞɚɧɢɟ	ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɣ
		2	ǜr2			ɦɨɳɧɨɫɬɢ ɊɗɆ, ɩɟɪɟɞɚɜɚɟɦɨɣ
		ǻɊ2=3ǜI2				ɜ ɪɨɬɨɪ, ɡɚ ɜɵɱɟɬɨɦ ɩɟɪɟɦɟɧ-
	ɊɆȿɏ= ɆɗɆǜȦ	ǻɊ2ȾɈȻ=3ǜI22ǜR2ȾɈȻ				ɧɵɯ ɩɨɬɟɪɶ ɜ ɚɤɬɢɜɧɨɦ ɫɨɩɪɨ-
						ɬɢɜɥɟɧɢɢ ɫɬɚɬɨɪɚ ǻɊ1 ɢ ɩɨ-
						ɫɬɨɹɧɧɵɯ, ɧɟ ɡɚɜɢɫɹɳɢɯ ɨɬ ɧɚ-
	Ɋȼ=ɆȼǜȦ	ǻɊɆȿɏ=ɊɆȿɏ–Ɋȼ				ɝɪɭɡɤɢ, ɩɨɬɟɪɶ ɜ ɫɬɚɥɢ ɫɬɚɬɨɪɚ
						ǻɊ1ɉɈɋɌ.
						ɗɥɟɤɬɪɨɦɚɝɧɢɬɧɚɹ				ɦɨɳ-
						ɧɨɫɬɶ ɊɗɆ ɩɪɟɨɛɪɚɡɭɟɬɫɹ, ɡɚ
	Ɋɢɫ. 3.70. ɗɧɟɪɝɟɬɢɱɟɫɤɚɹ ɞɢɚɝɪɚɦɦɚ					ɜɵɱɟɬɨɦ ɩɨɬɟɪɶ ɦɨɳɧɨɫɬɢ					ɜ
						ɚɤɬɢɜɧɨɦ	ɫɨɩɪɨɬɢɜɥɟɧɢɢ				ɪɨ
											-
	ɞɜɢɝɚɬɟɥɶɧɨɝɨ ɪɟɠɢɦɚ ȺȾ					ɬɨɪɚ ǻɊ2, ɜ ɦɟɯɚɧɢɱɟɫɤɭɸ
						ɦɨɳɧɨɫɬɶ	ɊɆȿɏ,		ɜɵɞɚɜɚɟɦɭɸ

ɧɚ ɜɚɥ Ɋȼ, ɡɚ ɜɵɱɟɬɨɦ ɦɟɯɚɧɢɱɟɫɤɢɯ ɩɨɬɟɪɶ ɜɧɭɬɪɢ ɞɜɢɝɚɬɟɥɹ ǻɊɆȿɏ.

Ɉɰɟɧɤɭ ɷɮɮɟɤɬɢɜɧɨɫɬɢ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɷɧɟɪɝɢɢ ɜɵɩɨɥɧɹɸɬ ɫ ɩɨɦɨɳɶɸ ɤɨɷɮɮɢɰɢɟɧɬɚ ɩɨɥɟɡɧɨɝɨ ɞɟɣɫɬɜɢɹ ɄɉȾ Ș = Ɋȼ / Ɋɋ.

ɇɚ ɪɢɫ. 3.71 ɩɪɢɜɟɞɟɧɚ ɡɚɜɢɫɢɦɨɫɬɶ Ș = f (Pȼ), ɩɨɫɬɪɨɟɧɧɚɹ ɩɪɢ ɪɚɛɨɬɟ ɞɜɢɝɚɬɟɥɹ ɧɚ ɟɫɬɟɫɬɜɟɧɧɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɟ. ɄɉȾ ɜ ɧɨɦɢɧɚɥɶɧɨɦ ɪɟɠɢɦɟ ɪɚɜɟɧ Șɇ = 0,75…0,95, ɩɪɢ ɭɜɟɥɢɱɟɧɢɢ ɧɨɦɢɧɚɥɶɧɨɣ ɦɨɳɧɨɫɬɢ Ɋɇ ɞɜɢɝɚɬɟɥɹ ɄɉȾ ɪɚɫ-

ɬɟɬ. ɉɪɢ ɧɚɪɚɫɬɚɧɢɢ ɧɚɝɪɭɡɤɢ							Școs ij1
					ȘȘ
ɧɚ ɜɚɥɭ ɄɉȾ ɪɚɫɬɟɬ ɜ ɫɜɹɡɢ ɫ
ɪɨɫɬɨɦ ɩɨɥɟɡɧɨɣ ɦɨɳɧɨɫɬɢ,				Șɇ			cos ij1ɇ
ɩɪɢ	Ɋȼ
		§ Ɋɇ ɄɉȾ ɞɨɫɬɢɝɚɟɬ
ɦɚɤɫɢɦɭɦɚ, ɩɪɢ			ɞɚɥɶɧɟɣɲɟɦ
ɪɨɫɬɟ	Ɋȼ	ɄɉȾ	ɫɧɢɠɚɟɬɫɹ ɜ
ɫɜɹɡɢ	ɫ	ɭɜɟɥɢɱɟɧɢɟɦ ɩɨɬɟɪɶ
ɦɨɳɧɨɫɬɢ ɜɧɭɬɪɢ ɦɚɲɢɧɵ.							cos ij10
Ⱦɪɭɝɢɦ ɩɨɤɚɡɚɬɟɥɟɦ, ɯɚ-						Ɋ			Ɋ
ɪɚɤɬɟɪɢɡɭɸɳɢɦ			ɦɚɲɢɧɭ ɩɟ-
						Ɋɇ		Ɋɇ
ɪɟɦɟɧɧɨɝɨ ɬɨɤɚ ɤɚɤ ɩɪɢɟɦɧɢɤ
ɷɥɟɤɬɪɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ, ɹɜɥɹ-						Ɋɢɫ. 3.71. ɗɧɟɪɝɟɬɢɱɟɫɤɢɟ
ɟɬɫɹ ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɳɧɨɫɬɢ,
						ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ȺȾ
ɭɱɢɬɵɜɚɸɳɢɣ ɷɮɮɟɤɬɢɜɧɨɫɬɶ

138

ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɚɤɬɢɜɧɨɣ ɷɧɟɪɝɢɢ. ɉɪɢ ɫɢɧɭɫɨɢɞɚɥɶɧɨɣ ɮɨɪɦɟ ɧɚɩɪɹɠɟɧɢɹ ɢ ɬɨɤɚ ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɳɧɨɫɬɢ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɨɬɧɨɲɟɧɢɟ ɚɤɬɢɜɧɨɣ ɦɨɳɧɨɫɬɢ P ɤ ɩɨɥɧɨɣ ɦɨɳɧɨɫɬɢ S, ɱɢɫɥɟɧɧɨ ɪɚɜɧɨɟ ɞɥɹ ɬɪɟɯɮɚɡɧɨɣ ɫɟɬɢ

cosij		P		3 PCɎ			.	(3.89)
				3 U
	1	S			I
				1Ɏ		1Ɏ

ɇɚ ɪɢɫ. 3.71 ɩɨɤɚɡɚɧɚ ɷɧɟɪɝɟɬɢɱɟɫɤɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ ɚɫɢɧɯɪɨɧɧɨɝɨ ɞɜɢɝɚɬɟɥɹ cos ij1 = f (Pȼ). ɉɪɢ ɪɚɛɨɬɟ ɜ ɪɟɠɢɦɚɯ, ɛɥɢɡɤɢɯ ɤ ɧɨɦɢɧɚɥɶɧɨɦɭ, ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɳɧɨɫɬɢ ɞɨɫɬɢɝɚɟɬ ɡɧɚɱɟɧɢɣ cos ij1 = 0,7…0,85. ȼ ɪɟɠɢɦɟ ɯɨɥɨɫɬɨɝɨ ɯɨɞɚ ɞɜɢɝɚɬɟɥɶ ɩɨɬɪɟɛɥɹɟɬ ɜ ɨɫɧɨɜɧɨɦ ɪɟɚɤɬɢɜɧɭɸ ɷɧɟɪɝɢɸ, cos ij10 = 0,05…0,15 ɭɱɢɬɵɜɚɟɬ ɩɨɬɪɟɛɥɟɧɢɟ ɚɤɬɢɜɧɨɣ ɷɧɟɪɝɢɢ ɧɚ ɩɨɤɪɵɬɢɟ ɩɨɬɟɪɶ ɷɧɟɪɝɢɢ ɜ ɞɜɢɝɚɬɟɥɟ. ɉɪɢ Ɋȼ > Ɋɇ ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɳɧɨɫɬɢ ɫɧɢɠɚɟɬɫɹ ɡɚ ɫɱɟɬ ɪɨɫɬɚ ɪɟɚɤɬɢɜɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ ɪɨɬɨɪɚ.

3.5.10.Ɍɨɪɦɨɡɧɵɟ ɪɟɠɢɦɵ

Ⱥɫɢɧɯɪɨɧɧɵɣ ɞɜɢɝɚɬɟɥɶ ɹɜɥɹɟɬɫɹ ɨɛɪɚɬɢɦɨɣ ɷɥɟɤɬɪɢɱɟɫɤɨɣ ɦɚɲɢɧɨɣ, ɫɩɨɫɨɛɧɨɣ ɪɚɛɨɬɚɬɶ ɤɚɤ ɜ ɞɜɢɝɚɬɟɥɶɧɨɦ, ɬɚɤ ɢ ɜ ɝɟɧɟɪɚɬɨɪɧɨɦ ɪɟɠɢɦɟ. ɉɪɢ ɩɨɹɜɥɟɧɢɢ ɧɚ ɜɚɥɭ ɢɡɛɵɬɨɱɧɨɣ ɦɟɯɚɧɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ ɞɜɢɝɚɬɟɥɶ ɩɟɪɟɯɨɞɢɬ ɜ ɝɟɧɟɪɚɬɨɪɧɵɣ ɪɟɠɢɦ.

ɋɬɨɱɤɢ ɡɪɟɧɢɹ ɩɨɬɪɟɛɥɟɧɢɹ ɢɡɛɵɬɨɱɧɨɣ ɷɥɟɤɬɪɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ ȺȾ ɪɚɛɨɬɚɟɬ

ɜɬɚɤɢɯ ɠɟ ɬɨɪɦɨɡɧɵɯ ɪɟɠɢɦɚɯ, ɤɚɤ ɢ ɪɚɫɫɦɨɬɪɟɧɧɵɣ ɪɚɧɟɟ ɞɜɢɝɚɬɟɥɶ ɩɨɫɬɨɹɧɧɨɝɨ ɬɨɤɚ: ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ, ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɬɨɪɦɨɠɟɧɢɹ ɢ ɬɨɪɦɨɠɟɧɢɹ ɩɪɨɬɢɜɨɜɤɥɸɱɟɧɢɟɦ.

Ɋɟɤɭɩɟɪɚɬɢɜɧɨɟ ɬɨɪɦɨɠɟɧɢɟ (ɊɌ) ɚɫɢɧɯɪɨɧɧɨɝɨ ɞɜɢɝɚɬɟɥɹ – ɢɡɛɵɬɨɱɧɚɹ ɚɤɬɢɜɧɚɹ ɷɥɟɤɬɪɢɱɟɫɤɚɹ ɷɧɟɪɝɢɹ ɜɨɡɜɪɚɳɚɟɬɫɹ ɜ ɫɟɬɶ ɡɚ ɜɵɱɟɬɨɦ ɩɨɬɟɪɶ ɜ ɫɬɚ-

		ɬɨɪɧɵɯ ɢ ɪɨɬɨɪɧɵɯ ɰɟɩɹɯ
		ɦɚɲɢɧɵ.		ɂɡɛɵɬɨɱɧɚɹ
Ɋ1=3ǜU1ǜI1ǜcosij1	ǻɊ1=3ǜI12ǜr1	ɦɨɳɧɨɫɬɶ ɫ ɜɚɥɚ ɞɜɢɝɚɬɟ-
		ɥɹ ɭɜɟɥɢɱɢɜɚɟɬ ɫɤɨɪɨɫɬɶ
		ɞɜɢɝɚɬɟɥɹ	ɞɨ	ɡɧɚɱɟɧɢɣ,
	ǻɊ1ɉɈɋɌ=3ǜI12ǜrμ	ɩɪɟɜɵɲɚɸɳɢɯ		ɫɤɨɪɨɫɬɶ
			ɦɚɝɧɢɬɧɨɝɨ ɩɨ-
		ɜɪɚɳɟɧɢɹ
		ɬɨɤɚ (ɫɢɧɯɪɨɧɧɭɸ ɫɤɨ-
ɊɗɆ=ɆɗɆǜȦ0	ǻɊ2=3ǜI22ǜr2	ɪɨɫɬɶ). ɉɪɨɜɨɞɧɢɤɢ ɪɨɬɨɪɚ
		ɨɩɟɪɟɠɚɸɬ ɩɨɥɟ ɫɬɚɬɨɪɚ ɢ
	ǻɊ2ȾɈȻ=3ǜI22ǜR2ȾɈȻ	ɜ ɧɢɯ ɧɚɜɨɞɢɬɫɹ ɗȾɋ, ɜɟɤ-
		ɬɨɪ ɤɨɬɨɪɨɣ ɦɟɧɹɟɬ ɧɚ-
		ɩɪɚɜɥɟɧɢɟ ɧɚ ɨɛɪɚɬɧɨɟ ɩɨ
	ǻɊɆȿɏ=Ɋȼ–ɊȼɆȿɏ	ɨɬɧɨɲɟɧɢɸ	ɤ	ɞɜɢɝɚɬɟɥɶ-
ɊɆȿɏ= ɆɗɆǜȦ		ɧɨɦɭ ɪɟɠɢɦɭ. ɉɨɹɜɥɹɟɬɫɹ
		ɬɨɤ ɪɨɬɨɪɚ, ɨɬ ɜɡɚɢɦɨɞɟɣ-
		ɫɬɜɢɹ ɬɨɤɚ ɪɨɬɨɪɚ ɫ ɩɨɬɨ-
Ɋȼ=ɆȼǜȦ		ɤɨɦ ɜɨɡɧɢɤɚɟɬ		ɬɨɪɦɨɡɧɨɣ
		ɦɨɦɟɧɬ. ɇɚ ɪɢɫ. 3.72 ɩɪɢ-
		ɜɟɞɟɧɚ	ɷɧɟɪɝɟɬɢɱɟɫɤɚɹ
Ɋɢɫ. 3.72. ɗɧɟɪɝɟɬɢɱɟɫɤɚɹ ɞɢɚɝɪɚɦɦɚ		ɞɢɚɝɪɚɦɦɚ	ɪɟɠɢɦɚ ɪɟɤɭ-
ɪɟɠɢɦɚ ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ		ɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ.

ɇɚɩɪɚɜɥɟɧɢɟ ɩɨɬɨɤɚ ɦɨɳ

139

ɧɨɫɬɢ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɞɜɢɝɚɬɟɥɶɧɵɦ ɪɟɠɢɦɨɦ – ɨɛɪɚɬɧɨɟ, ɫ ɜɚɥɚ ɞɜɢɝɚɬɟɥɹ ɜ ɫɟɬɶ.

ɉɪɢ ɩɟɪɟɯɨɞɟ ɜ ɪɟɠɢɦ ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ ɞɜɢɝɚɬɟɥɶ ɩɪɨɯɨɞɢɬ ɯɚɪɚɤɬɟɪɧɵɟ ɬɨɱɤɢ:

1)ɯɨɥɨɫɬɨɣ ɯɨɞ (Ɋȼ = 0) – ɩɨɬɟɪɢ ɦɨɳɧɨɫɬɢ ɜ ɦɚɲɢɧɟ ɩɨɤɪɵɜɚɸɬɫɹ ɫɨ ɫɬɨɪɨɧɵ ɫɟɬɢ;

2)ɢɞɟɚɥɶɧɵɣ ɯɨɥɨɫɬɨɣ ɯɨɞ – ɗȾɋ ɢ ɬɨɤ ɪɨɬɨɪɚ ɪɚɜɧɵ ɧɭɥɸ, ɆɗɆ = 0, ɦɟɯɚɧɢɱɟɫɤɢɟ ɩɨɬɟɪɢ ɩɨɤɪɵɜɚɸɬɫɹ ɫ ɜɚɥɚ ɞɜɢɝɚɬɟɥɹ, ɩɨɬɟɪɢ ɦɨɳɧɨɫɬɢ ɜ ɰɟɩɢ ɫɬɚɬɨɪɚ ɩɨɬɪɟɛɥɹɸɬɫɹ ɢɡ ɫɟɬɢ;

3)ɚɤɬɢɜɧɚɹ ɦɨɳɧɨɫɬɶ, ɩɨɬɪɟɛɥɹɟɦɚɹ ɢɡ ɫɟɬɢ, ɪɚɜɧɚ ɧɭɥɸ Ɋ1 = 0, ɩɨɬɟɪɢ ɦɨɳɧɨɫɬɢ ɜ ɰɟɩɹɯ ɦɚɲɢɧɵ ɩɨɤɪɵɜɚɸɬɫɹ ɫɨ ɫɬɨɪɨɧɵ ɜɚɥɚ ɞɜɢɝɚɬɟɥɹ.

Ɋɟɠɢɦ ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ ɧɚɱɢɧɚɟɬɫɹ ɩɪɢ ɫɤɨɪɨɫɬɢ Ȧ > Ȧ0ɇ, ɤɨɝɞɚ ɦɟɧɹɟɬɫɹ ɧɚɩɪɚɜɥɟɧɢɟ ɚɤɬɢɜɧɨɣ ɦɨɳɧɨɫɬɢ Ɋ1 < 0.

ȼɚɪɢɚɧɬɵ ɨɛɟɫɩɟɱɟɧɢɹ ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ ɩɨɯɨɠɢ ɧɚ ɚɧɚɥɨɝɢɱɧɵɟ ɞɥɹ Ⱦɇȼ, ɟɫɥɢ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɪɚɛɨɱɢɣ ɭɱɚɫɬɨɤ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ

(ɫɦ. ɪɢɫ. 3.19):

1)ɢɡɦɟɧɟɧɢɟ ɡɧɚɤɚ ɫɬɚɬɢɱɟɫɤɨɝɨ ɦɨɦɟɧɬɚ ɨɬ Ɇɋ ɧɚ Ɇɋ1 < 0, ɞɜɢɝɚɬɟɥɶ ɩɟɪɟɯɨɞɢɬ ɢɡ ɞɜɢɝɚɬɟɥɶɧɨɝɨ ɪɟɠɢɦɚ ɪɚɛɨɬɵ ɜ ɪɟɠɢɦ ɪɟɤɭɩɟɪɚɰɢɢ ɱɟɪɟɡ ɬɨɱɤɭ ɫɢɧɯɪɨɧɧɨɣ ɫɤɨɪɨɫɬɢ Ȧ0;

2)ɫɩɭɫɤ ɝɪɭɡɚ – ɩɪɢ ɧɟɢɡɦɟɧɧɨɦ ɡɧɚɤɟ Ɇɋ ɞɜɢɝɚɬɟɥɶ ɜɪɚɳɚɟɬɫɹ ɜ ɨɛɪɚɬɧɭɸ ɫɬɨɪɨɧɭ, ɢ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɝɪɭɡɚ ɩɟɪɟɯɨɞɢɬ ɜ ɪɟɠɢɦ ɪɟɤɭɩɟɪɚɰɢɢ ɫɨ ɫɤɨɪɨɫɬɶɸ ɜɵɲɟ ɫɢɧɯɪɨɧɧɨɣ ɫɤɨɪɨɫɬɢ (Ȧ > Ȧ0ɇ);

3)ɩɪɢ ɫɧɢɠɟɧɢɢ ɱɚɫɬɨɬɵ ɧɚɩɪɹɠɟɧɢɹ ɧɚ ɫɬɚɬɨɪɟ (ɜɚɪɢɚɧɬ ɩɢɬɚɧɢɹ ɞɜɢɝɚɬɟɥɹ

ɨɬ ɩɪɟɨɛɪɚɡɨɜɚɬɟɥɹ ɱɚɫɬɨɬɵ) ɫɧɢɠɚɟɬɫɹ ɫɢɧɯɪɨɧɧɚɹ ɫɤɨɪɨɫɬɶ Ȧ0 < Ȧ0ɇ. Ⱦɜɢɝɚɬɟɥɶ ɨɫɭɳɟɫɬɜɥɹɟɬ ɩɟɪɟɯɨɞ ɢɡ ɞɜɢɝɚɬɟɥɶɧɨɝɨ ɪɟɠɢɦɚ ɪɚɛɨɬɵ ɜ ɪɟɠɢɦ ɪɟɤɭɩɟɪɚɰɢɢ. ɇɚ ɭɱɚɫɬɤɟ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ – ɨɬ ɧɚɱɚɥɶɧɨɣ ɫɤɨɪɨɫɬɢ ɞɨ Ȧ0

–ɞɜɢɝɚɬɟɥɶ ɪɚɛɨɬɚɟɬ ɜ ɪɟɠɢɦɟ ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ.

Ɇɟɯɚɧɢɱɟɫɤɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ ɩɪɢ ɊɌ ɹɜɥɹɟɬɫɹ ɩɪɨɞɨɥɠɟɧɢɟɦ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɞɜɢɝɚɬɟɥɶɧɨɝɨ ɪɟɠɢɦɚ ɜɨ ɜɬɨɪɨɣ (ɢɥɢ ɱɟɬɜɟɪɬɵɣ) ɤɜɚɞɪɚɧɬ. ȼɵɪɚɠɟɧɢɟ ɦɟɯɚɧɢɱɟɫɤɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ (3.61) ɧɟ ɢɡɦɟɧɹɟɬɫɹ, ɢɡɦɟɧɹɟɬɫɹ ɥɢɲɶ ɡɧɚɤ ɫɤɨɥɶɠɟɧɢɹ.

Ⱦɨɫɬɨɢɧɫɬɜɚ ɪɟɠɢɦɚ ɊɌ ɚɧɚɥɨɝɢɱɧɵ ɪɟɠɢɦɭ ɊɌ Ⱦɇȼ:

1)ɠɺɫɬɤɢɟ ɦɟɯɚɧɢɱɟɫɤɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ;

2)ɜɵɫɨɤɚɹ ɷɤɨɧɨɦɢɱɧɨɫɬɶ, ɢɡɛɵɬɨɱɧɚɹ ɷɥɟɤɬɪɢɱɟɫɤɚɹ ɷɧɟɪɝɢɹ ɜɨɡɜɪɚɳɚɟɬɫɹ

ɜɫɟɬɶ.

3)ɧɟɨɛɯɨɞɢɦɨɫɬɶ ɧɚɥɢɱɢɹ ɩɨɬɪɟɛɢɬɟɥɹ ɷɧɟɪɝɢɢ ɪɟɤɭɩɟɪɚɰɢɢ ɨɬɩɚɞɚɟɬ ɩɪɢ ɪɚɫɩɪɟɞɟɥɟɧɢɢ ɷɥɟɤɬɪɨɷɧɟɪɝɢɢ ɧɚ ɩɟɪɟɦɟɧɧɨɦ ɬɨɤɟ.

ɇɟɞɨɫɬɚɬɤɨɦ ɪɟɠɢɦɚ ɊɌ ɹɜɥɹɟɬɫɹ ɩɨɬɪɟɛɥɟɧɢɟ ɢɡ ɫɟɬɢ ɪɟɚɤɬɢɜɧɨɣ ɷɧɟɪɝɢɢ ɩɪɢ ɜɨɡɜɪɚɳɟɧɢɢ ɜ ɫɟɬɶ ɚɤɬɢɜɧɨɣ ɷɧɟɪɝɢɢ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɬɨɤɨɜɚɹ ɧɚɝɪɭɡɤɚ ɫɟɬɢ ɩɪɚɤɬɢɱɟɫɤɢ ɧɟ ɫɧɢɠɚɟɬɫɹ;

Ɉɛɥɚɫɬɶ ɩɪɢɦɟɧɟɧɢɹ ɪɟɤɭɩɟɪɚɬɢɜɧɨɝɨ ɬɨɪɦɨɠɟɧɢɹ ɨɝɪɚɧɢɱɟɧɚ ɝɪɭɡɨɩɨɞɴɟɦɧɵɦɢ ɦɟɯɚɧɢɡɦɚɦɢ (ɤɪɚɧɵ, ɥɢɮɬɵ ɢ ɬ.ɩ.) ɢ ɫɢɫɬɟɦɚɦɢ ɫ ɢɧɞɢɜɢɞɭɚɥɶɧɵɦɢ ɩɪɟɨɛɪɚɡɨɜɚɬɟɥɹɦɢ (ɉɑ – ȺȾ).

Ɍɨɪɦɨɠɟɧɢɟ ɩɪɨɬɢɜɨɜɤɥɸɱɟɧɢɟɦ (ɉȼ). Ɋɟɠɢɦ ɩɪɨɬɢɜɨɜɤɥɸɱɟɧɢɹ – ɬɨɪ-

ɦɨɡɧɨɣ ɪɟɠɢɦ, ɤɨɝɞɚ ɞɜɢɝɚɬɟɥɶ ɜɤɥɸɱɟɧ ɞɥɹ ɨɞɧɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ ɜɪɚɳɟɧɢɹ, ɧɨ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɜɧɟɲɧɢɯ ɫɢɥ ɜɪɚɳɚɟɬɫɹ ɜ ɩɪɨɬɢɜɨɩɨɥɨɠɧɭɸ ɫɬɨɪɨɧɭ.

Ⱦɜɢɝɚɬɟɥɶ ɩɨɥɭɱɚɟɬ ɢɡɛɵɬɨɱɧɭɸ ɦɟɯɚɧɢɱɟɫɤɭɸ ɷɧɟɪɝɢɸ ɫ ɜɚɥɚ, ɩɪɟɨɛɪɚɡɭɟɬ ɟɟ ɜ ɷɥɟɤɬɪɢɱɟɫɤɭɸ ɷɧɟɪɝɢɸ. ɋɬɚɬɨɪ ɞɜɢɝɚɬɟɥɹ ɞɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɪɟɠɢɦɚ ɉȼ

140