Лабораторная работа № 3 спектральный анализ сигналов

Цель работы: ознакомление со спектральным описанием периодических функций с помощью рядов Фурье.

Необходимые теоретические сведения. Разложение в ряд Фурье

Первым рассматриваемым сигналом будет последовательность прямоугольных импульсов с амплитудой А, длительностью и периодом повторенияТ. Начало отсчета времени примем расположенным в середине импульса (рис.1).

Рис 1. - Периодическая последовательность прямоугольных импульсов

Данный сигнал является четной функцией, поэтому для его представления удобнее использовать синусно-косинусную форму ряда Фурье— в ней будут присутствовать только косинусные слагаемые , равные

Введем скважность в полученную формулу для коэффициентов ряда Фурье, а затем приведем формулу к виду .

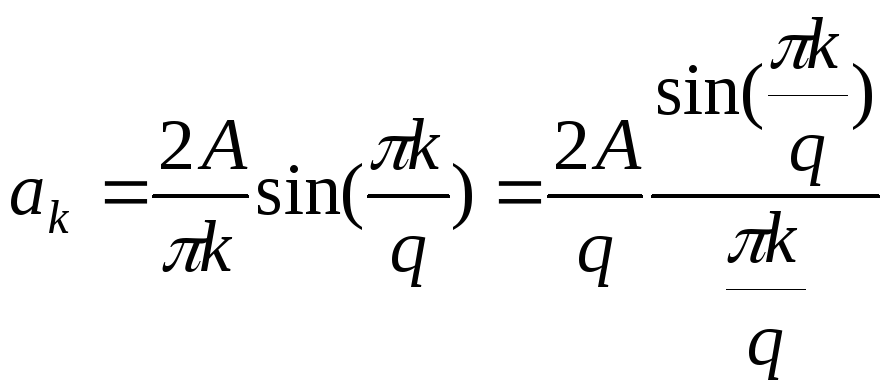
Представление последовательности прямоугольных импульсов в виде ряда Фурье имеет вид:

Амплитуды гармонических слагаемых ряда зависят от номера гармоники по закону (см. рис. 2).График функции имеет лепестковый характер. Итак, ширина лепестков, измеренная в количестве гармоник, равна скважности последовательности (при имеем, если). Отсюда следует важное свойство спектра последовательности прямоугольных импульсов — в нем отсутствуют (имеют нулевые амплитуды) гармоники с номерами, кратными скважности.

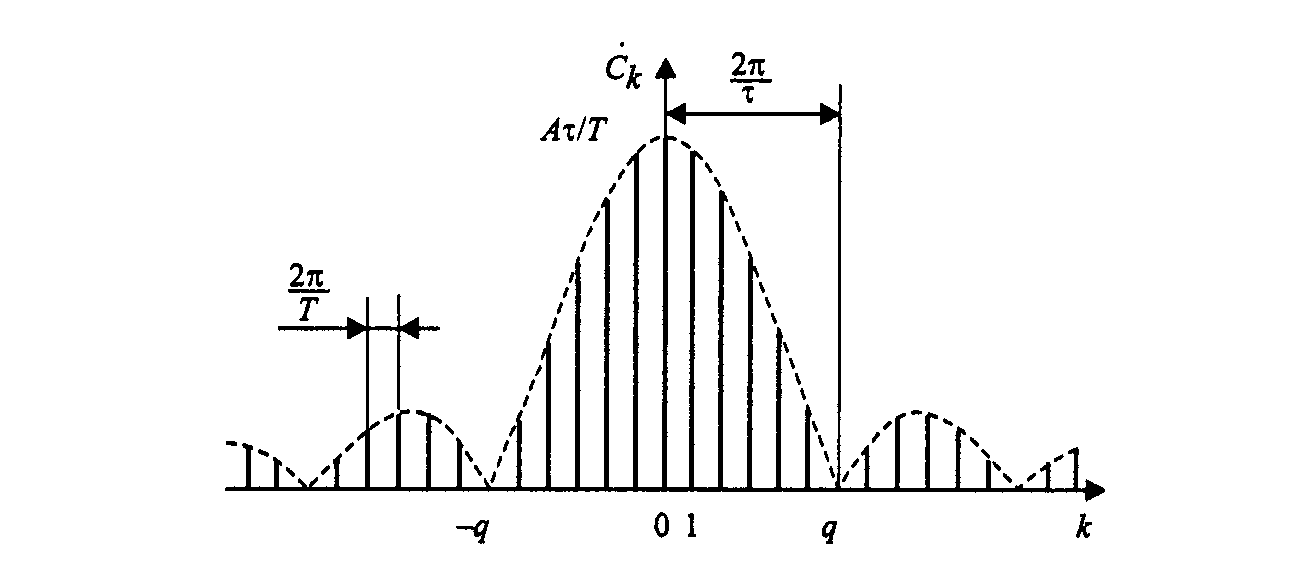
Рис. 2 - Коэффициенты ряда Фурье для последовательности прямоугольных импульсов.

Расстояние по частоте между соседними гармониками равно частоте следования импульсов — . Ширина лепестков спектра, измеренная в единицах частоты, равна , то есть обратно пропорциональна длительности импульсов, т.е. чем короче сигнал, тем шире его спектр.

Важным частным случаем предыдущего сигнала является меандр (рис. 3) — последова­тельность прямоугольных импульсов со скважностью, равной , когда дли­тельности импульсов и промежутков между ними становятся равными.

Рис. 3 - Меандр

Тогда,

,

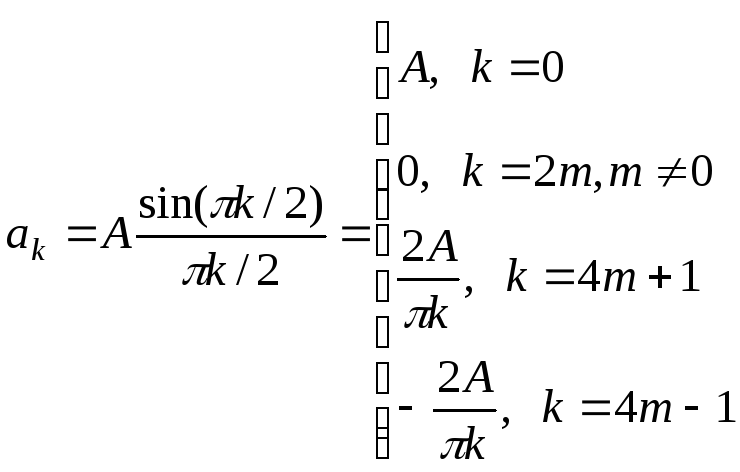где m – произвольное целое число.

Таким образом, в спектре меандра присутствуют только нечетные гармоники. Представление меандра в виде ряда Фурье с учетом этого может быть записано следующим образом:

.

Гармонические составляющие, из которых складывается меандр, имеют ампли­туды, обратно пропорциональные номерам гармоник, и чередующиеся знаки. На примыкающих к разрыву участках сумма ряда Фурье дает заметные пульса­ции. Это явление, присущее ря­дам Фурье для любых сигналов с разрывами первого рода (скачками), называет­ся эффектом Гиббса. Можно показать, что амплитуда первого (самого большого) выброса составляет примерно 9 % от величины скачка.

Рисунок 4. Эффект Гиббса.

Пилообразный сигнал (рис. 5). в пре­делах периода описывается линейной функцией:

, .

Данный сигнал является нечетной функцией, поэтому его ряд Фурье в синусно-косинусной форме будет содержать только синусные слагаемые:

.

Сам ряд Фурье для пилообразного сигнала выглядит следующим образом:

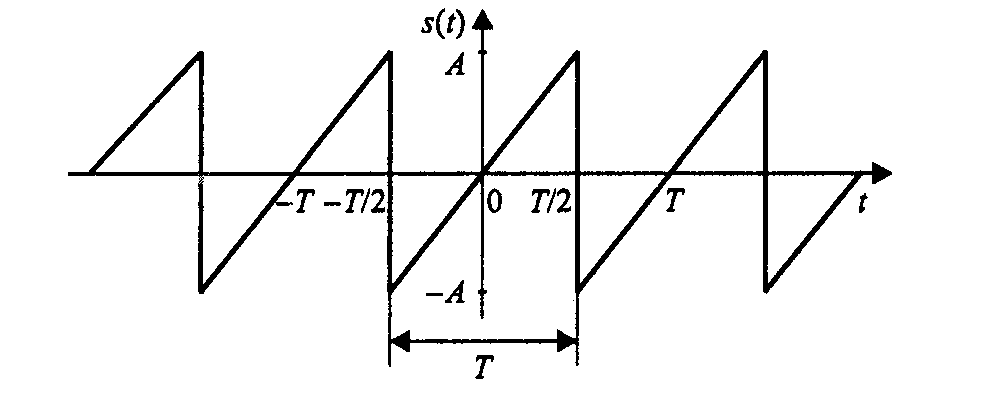
Рис. 5 - Пилообразный сигнал.

Периодическая последовательность треугольных импульсов имеет симметричную форму (рис. 6):

, .

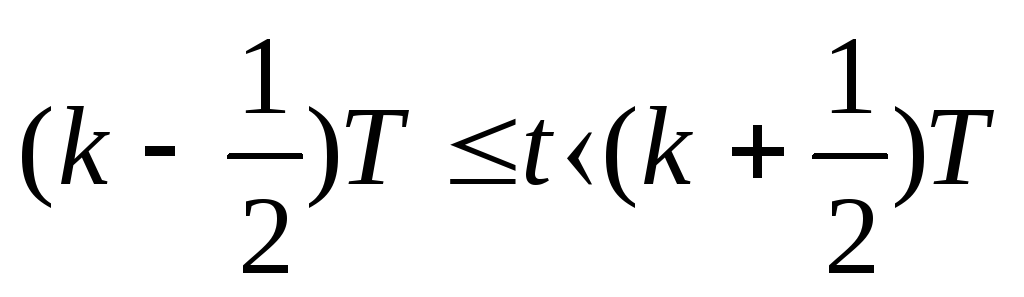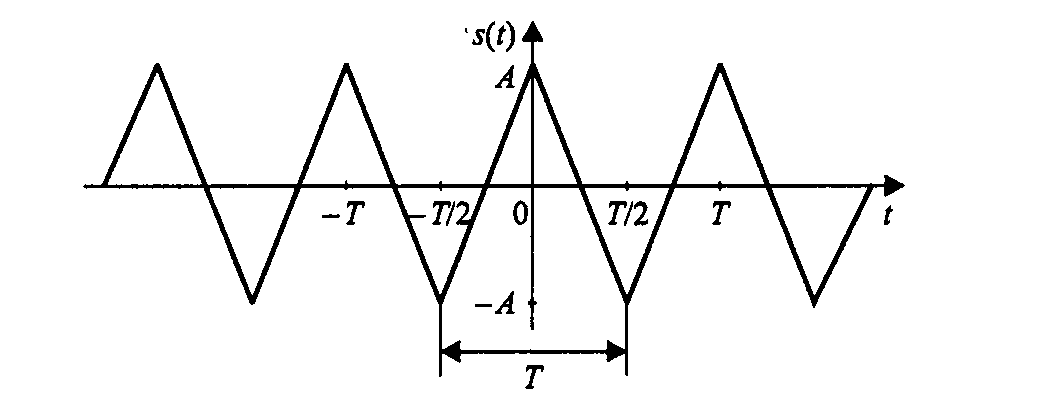
Рис. 6 - Последовательность треугольных импульсов.

Ряд Фурье имеет следующий вид:

.

Рассмотрим программу, реализующую разложение в ряд Фурье прямоугольной последовательности импульсов.

» N = 8; % число ненулевых гармоник

» t = -1:0.01:1; % вектор моментов времени

» А = 1; % амплитуда

» Т = 1; % период

» nh = (1:N)*2-1; % номера ненулевых гармоник

» % строки - гармоники

» harmonics = cos(2*pi*nh'*t/T);

» Am = 2/pi./nh; % амплитуды гармоник

» Am(2:2:end) = -Am(2:2:end); % чередование знаков

» s1 =harmonics .* repmat(Am', 1, length(t));

» % строки - частичные суммы гармоник

» s2 = cumsum(s1);

» for k=1:N, subplot(ceil(N/2),2, k), plot(t,s2(k,:)),end

ЗАДАНИЕ1.